鲁教版(五四制)八年级下册第六章特 殊平行四边形单元测试题(二)(含答案)
文档属性
| 名称 | 鲁教版(五四制)八年级下册第六章特 殊平行四边形单元测试题(二)(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 219.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-10 00:00:00 | ||
图片预览

文档简介
第六章 特殊平行四边形测试题(二)
一、选择题(每小题3分,共30分)
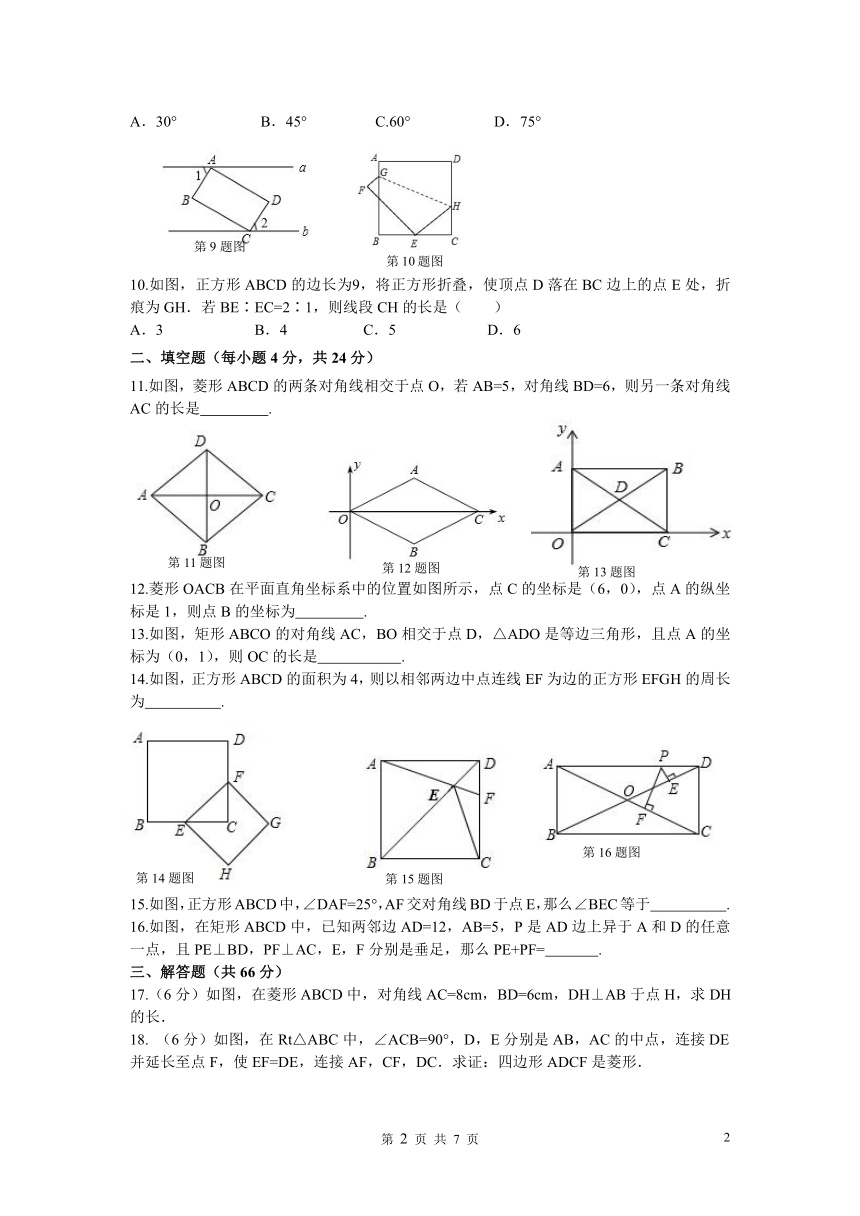
1.如图,菱形ABCD的边长为2cm,则它的周长是( )
A.4cm B.6cm C.8cm D.10cm
2.如图,在菱形ABCD中,AB=3,∠ABC=60°,则对角线AC的长为( )
A.12 B.9 C.6 D.3
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形.其中一定成立的是( )
①② B.①③ C.②③ D.③④
4.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直且相等
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,若OA=2,则BD的长为( )
A.4 B.3 C.2 D.1
6.若顺次连接四边形ABCD四边的中点,得到的图形是一个菱形,则四边形ABCD一定是
A.矩形 B.菱形
C.对角线互相垂直的四边形 D.对角线相等的四边形
7.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠1=∠2
8.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别记为S1,S2,则S1,S2的大小关系是( )
A.S1>S2 B.S1=S2 C.S1<S2 D.3S1=2S2
9.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=60°,则∠2的度数为( )
A.30° B.45° C.60° D.75°
10.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是( )
A.3 B.4 C.5 D.6
二、填空题(每小题4分,共24分)
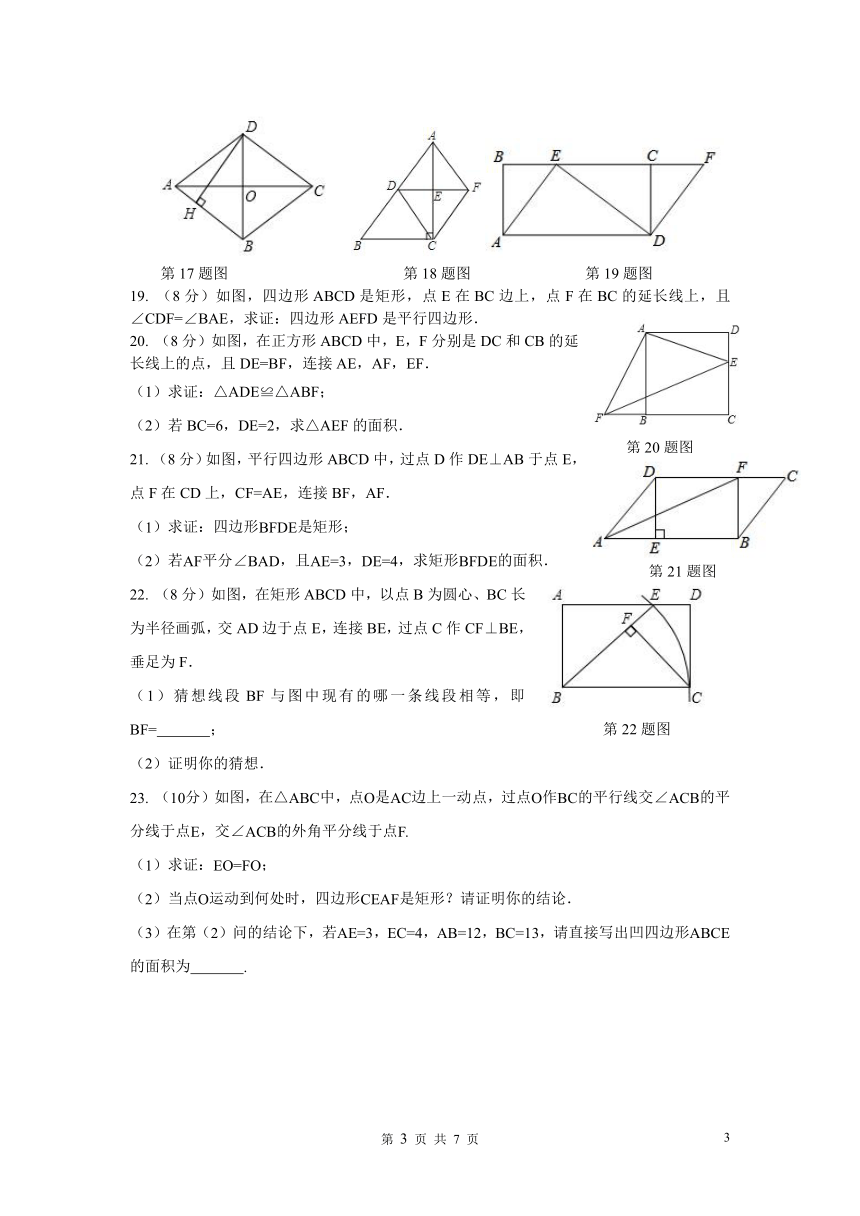
如图,菱形ABCD的两条对角线相交于点O,若AB=5,对角线BD=6,则另一条对角线AC的长是 .
12.菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标为 .
13.如图,矩形ABCO的对角线AC,BO相交于点D,△ADO是等边三角形,且点A的坐标为(0,1),则OC的长是 .
14.如图,正方形ABCD的面积为4,则以相邻两边中点连线EF为边的正方形EFGH的周长为 .
15.如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,那么∠BEC等于 .
16.如图,在矩形ABCD中,已知两邻边AD=12,AB=5,P是AD边上异于A和D的任意一点,且PE⊥BD,PF⊥AC,E,F分别是垂足,那么PE+PF= .
三、解答题(共66分)
17.(6分)如图,在菱形ABCD中,对角线AC=8cm,BD=6cm,DH⊥AB于点H,求DH的长.
18. (6分)如图,在Rt△ABC中,∠ACB=90°,D,E分别是AB,AC的中点,连接DE并延长至点F,使EF=DE,连接AF,CF,DC.求证:四边形ADCF是菱形.
第17题图 第18题图 第19题图
19. (8分)如图,四边形ABCD是矩形,点E在BC边上,点F在BC的延长线上,且∠CDF=∠BAE,求证:四边形AEFD是平行四边形.
20. (8分)如图,在正方形ABCD中,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)若BC=6,DE=2,求△AEF的面积.
21. (8分)如图,平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
22. (8分)如图,在矩形ABCD中,以点B为圆心、BC长为半径画弧,交AD边于点E,连接BE,过点C作CF⊥BE,垂足为F.
(1)猜想线段BF与图中现有的哪一条线段相等,即BF= ;
(2)证明你的猜想.
23. (10分)如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论.
(3)在第(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,请直接写出凹四边形ABCE的面积为 .
第23题图 第24题图
24. (10分)如图,△ABC中,D是BC边上任意一点,DE∥AC,DF∥AB.
(1)试说明四边形AEDF的形状,并说明理由.
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形?为什么?
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形?不需说明理由.
25. (10分)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15),过点D作DF⊥BC于点F,连接DE,EF.
(1)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(2)当t为何值时,△DEF为直角三角形?
第25题图
参考答案:
一、1.C 2.D. 3.B 4.A 5.A 6.D 7.C 8.B 9.C 10.B
二、11.8 12.(3,-1) 13. 14. 15. 70°
16. 提示:如图,过点A作AG⊥BD于点G,则S△AOD=·OD·AG,S△AOP+S△POD=·AO·PF+·DO·PE=·DO·(PE+PF).
因为S△AOD=S△AOP+S△POD,所以PE+PF=AG.
因为AD=12,AB=5,所以BD=13,OD=,S△AOD=15.
所以15=AG,则 AG=,即PE+PF=.
三、17.解:因为四边形ABCD是菱形,AC=8cm,BD=6cm,
所以AC⊥BD,OA=AC=4cm,OB=BD=3cm,在Rt△AOB中,
AB2=AO2+BO2=42+32=25,所以AB=5.
因为DH⊥AB,S菱形ABCD=AC?BD=AB?DH,即×6×8=5DH,所以DH=.
18.证明:因为点E是边AC的中点,所以AE=EC.
又因为EF=DE,所以四边形ADCF是平行四边形.
因为点D,E分别是边AB,AC的中点,所以DE是△ABC的中位线,所以DE∥BC.
因为∠ACB=90°,所以∠AED=90°.所以AC⊥DF.所以四边形ADCF是菱形.
19.证明:因为四边形ABCD是矩形,所以AB=DC,∠B=∠DCF=90°.
又因为∠BAE=∠CDF,所以△ABE≌△DCF,所以AE=DF,BE=CF,所以BC=EF.
又因为BC=AD,所以EF=AD.所以四边形AEFD是平行四边形.
20.(1)证明:因为四边形ABCD是正方形,所以AD=AB,∠D=∠ABF=90°.
又DE=BF,所以△ADE≌△ABF.
(2)解:因为BC=6,所以AD=6.
在Rt△ADE中,DE=2,AD=6,所以AE2=AD2+DE2=40.
由(1)△ADE≌△ABF,得∠EAD=∠FAB,AE=AF.
因为∠EAD+∠BAE=90°,所以∠FAB+∠BAE=90°,所以∠EAF=90°.
因为AE=AF,所以△AEF的面积=AE2=×40=20.
21. (1)证明:因为四边形ABCD是平行四边形,所以AB=CD,AB∥CD,所以DF∥BE.
因为CF=AE,所以DF=BE,所以四边形BFDE是平行四边形.
又因为DE⊥AB,所以∠DEB=90°,所以四边形BFDE是矩形.
(2)解:因为AB∥CD,所以∠BAF=∠AFD.
因为AF平分∠BAD,所以∠BAF=∠DAF,所以∠DAF=∠AFD,所以AD=DF.
在Rt△ADE中,因为AE=3,DE=4,所以AD=5,则DF=5.所以矩形BFDE的面积为5×4=20.
22.(1)EA
(2)证明:在矩形ABCD中,AD∥BC,∠A=90°,所以∠AEB=∠FBC.
因为CF⊥BE,所以∠CFB=∠A=90°.
由作图可知,BC=BE,所以△BFC≌△EAB,所以BF=EA.
23.(1)证明:因为EF∥BC,所以∠OEC=∠BCE.
因为CE平分∠ACB,所以∠BCE=∠OCE,所以∠OEC=∠OCE,所以EO=CO.
同理FO=CO,所以EO=FO.
(2)解:当点O运动到AC的中点时,四边形CEAF是矩形.
证明:由(1)得EO=FO.
因为O是AC的中点,所以AO=CO,所以四边形CEAF是平行四边形.
因为EO=FO=CO,所以EO=FO=AO=CO,即EF=AC,所以四边形CEAF是矩形.
(3)24 提示:由(2)得四边形CEAF是矩形,所以∠AEC=90°.
又AE=3,EC=4,所以AC=5,S△ACE =×3×4=6.
又因为AB=12,BC=13,所以122+52=132,所以△ABC是直角三角形,且∠BAC=90°.
所以S△ABC =×12×5=30,所以S四边形ABCE =S△ABC -S△ACE =30-6=24.
24.解:(1)四边形AEDF为平行四边形.理由如下:
因为DE∥AC,DF∥AB,所以四边形AEDF为平行四边形.
(2)当AD平分∠BAC时,四边形AEDF为菱形.理由如下:
因为DF∥AB,所以∠FDA=∠EAD.
因为AD平分∠BAC,所以∠FAD=∠EAD,所以∠FDA=∠FAD,所以AF=DF.
因为四边形AEDF为平行四边形,所以四边形AEDF为菱形.
(3)当△ABC满足∠CAB=90°时,四边形AEDF为正方形.
25.解:(1)能.理由如下:
在△DFC中,∠DFC=90°,∠C=30°,DC=4t,所以DF=2t.因为AE=2t,所以AE=DF.
因为AB⊥BC,DF⊥BC,所以AE∥DF.所以四边形AEFD为平行四边形.
当AE=AD时,四边形AEFD为菱形,即60-4t=2t,解得t=10.
所以当t=10 s时,四边形AEFD为菱形.
(2)①当∠DEF=90°时,由(1)知四边形AEFD为平行四边形,所以EF∥AD,
所以∠ADE=∠DEF=90°.
因为∠A=60°,所以∠AED=30°,所以AD=AE=t.
又AD=60-4t,即60-4t=t,解得t=12;
②当∠EDF=90°时,易得四边形EBFD为矩形.在Rt△AED中,∠A=60°,则∠ADE=30°,
所以AD=2AE,即60-4t=4t,解得t=.
③若∠EFD=90°,则E与B重合,D与A重合,此种情况不存在.
综上所述,当t=12 s或 s时,△DEF为直角三角形.
第3题图
第2题图
第1题图
第8题图
第7题图
第5题图
第10题图
第9题图
第13题图
第11题图
第12题图
(第13题图)
第14题图
第15题图
第16题图
第20题图
第21题图
第22题图
PAGE
1
一、选择题(每小题3分,共30分)
1.如图,菱形ABCD的边长为2cm,则它的周长是( )
A.4cm B.6cm C.8cm D.10cm
2.如图,在菱形ABCD中,AB=3,∠ABC=60°,则对角线AC的长为( )
A.12 B.9 C.6 D.3
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形.其中一定成立的是( )
①② B.①③ C.②③ D.③④
4.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.对角线互相垂直且相等
5.如图,在矩形ABCD中,对角线AC,BD相交于点O,若OA=2,则BD的长为( )
A.4 B.3 C.2 D.1
6.若顺次连接四边形ABCD四边的中点,得到的图形是一个菱形,则四边形ABCD一定是
A.矩形 B.菱形
C.对角线互相垂直的四边形 D.对角线相等的四边形
7.如图,要使平行四边形ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠1=∠2
8.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别记为S1,S2,则S1,S2的大小关系是( )
A.S1>S2 B.S1=S2 C.S1<S2 D.3S1=2S2
9.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=60°,则∠2的度数为( )
A.30° B.45° C.60° D.75°
10.如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是( )
A.3 B.4 C.5 D.6
二、填空题(每小题4分,共24分)
如图,菱形ABCD的两条对角线相交于点O,若AB=5,对角线BD=6,则另一条对角线AC的长是 .
12.菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标为 .
13.如图,矩形ABCO的对角线AC,BO相交于点D,△ADO是等边三角形,且点A的坐标为(0,1),则OC的长是 .
14.如图,正方形ABCD的面积为4,则以相邻两边中点连线EF为边的正方形EFGH的周长为 .
15.如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于点E,那么∠BEC等于 .
16.如图,在矩形ABCD中,已知两邻边AD=12,AB=5,P是AD边上异于A和D的任意一点,且PE⊥BD,PF⊥AC,E,F分别是垂足,那么PE+PF= .
三、解答题(共66分)
17.(6分)如图,在菱形ABCD中,对角线AC=8cm,BD=6cm,DH⊥AB于点H,求DH的长.
18. (6分)如图,在Rt△ABC中,∠ACB=90°,D,E分别是AB,AC的中点,连接DE并延长至点F,使EF=DE,连接AF,CF,DC.求证:四边形ADCF是菱形.
第17题图 第18题图 第19题图
19. (8分)如图,四边形ABCD是矩形,点E在BC边上,点F在BC的延长线上,且∠CDF=∠BAE,求证:四边形AEFD是平行四边形.
20. (8分)如图,在正方形ABCD中,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(2)若BC=6,DE=2,求△AEF的面积.
21. (8分)如图,平行四边形ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
22. (8分)如图,在矩形ABCD中,以点B为圆心、BC长为半径画弧,交AD边于点E,连接BE,过点C作CF⊥BE,垂足为F.
(1)猜想线段BF与图中现有的哪一条线段相等,即BF= ;
(2)证明你的猜想.
23. (10分)如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论.
(3)在第(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,请直接写出凹四边形ABCE的面积为 .
第23题图 第24题图
24. (10分)如图,△ABC中,D是BC边上任意一点,DE∥AC,DF∥AB.
(1)试说明四边形AEDF的形状,并说明理由.
(2)连接AD,当AD满足什么条件时,四边形AEDF为菱形?为什么?
(3)在(2)的条件下,当△ABC满足什么条件时,四边形AEDF为正方形?不需说明理由.
25. (10分)如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t≤15),过点D作DF⊥BC于点F,连接DE,EF.
(1)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(2)当t为何值时,△DEF为直角三角形?
第25题图
参考答案:
一、1.C 2.D. 3.B 4.A 5.A 6.D 7.C 8.B 9.C 10.B
二、11.8 12.(3,-1) 13. 14. 15. 70°
16. 提示:如图,过点A作AG⊥BD于点G,则S△AOD=·OD·AG,S△AOP+S△POD=·AO·PF+·DO·PE=·DO·(PE+PF).
因为S△AOD=S△AOP+S△POD,所以PE+PF=AG.
因为AD=12,AB=5,所以BD=13,OD=,S△AOD=15.
所以15=AG,则 AG=,即PE+PF=.
三、17.解:因为四边形ABCD是菱形,AC=8cm,BD=6cm,
所以AC⊥BD,OA=AC=4cm,OB=BD=3cm,在Rt△AOB中,
AB2=AO2+BO2=42+32=25,所以AB=5.
因为DH⊥AB,S菱形ABCD=AC?BD=AB?DH,即×6×8=5DH,所以DH=.
18.证明:因为点E是边AC的中点,所以AE=EC.
又因为EF=DE,所以四边形ADCF是平行四边形.
因为点D,E分别是边AB,AC的中点,所以DE是△ABC的中位线,所以DE∥BC.
因为∠ACB=90°,所以∠AED=90°.所以AC⊥DF.所以四边形ADCF是菱形.
19.证明:因为四边形ABCD是矩形,所以AB=DC,∠B=∠DCF=90°.
又因为∠BAE=∠CDF,所以△ABE≌△DCF,所以AE=DF,BE=CF,所以BC=EF.
又因为BC=AD,所以EF=AD.所以四边形AEFD是平行四边形.
20.(1)证明:因为四边形ABCD是正方形,所以AD=AB,∠D=∠ABF=90°.
又DE=BF,所以△ADE≌△ABF.
(2)解:因为BC=6,所以AD=6.
在Rt△ADE中,DE=2,AD=6,所以AE2=AD2+DE2=40.
由(1)△ADE≌△ABF,得∠EAD=∠FAB,AE=AF.
因为∠EAD+∠BAE=90°,所以∠FAB+∠BAE=90°,所以∠EAF=90°.
因为AE=AF,所以△AEF的面积=AE2=×40=20.
21. (1)证明:因为四边形ABCD是平行四边形,所以AB=CD,AB∥CD,所以DF∥BE.
因为CF=AE,所以DF=BE,所以四边形BFDE是平行四边形.
又因为DE⊥AB,所以∠DEB=90°,所以四边形BFDE是矩形.
(2)解:因为AB∥CD,所以∠BAF=∠AFD.
因为AF平分∠BAD,所以∠BAF=∠DAF,所以∠DAF=∠AFD,所以AD=DF.
在Rt△ADE中,因为AE=3,DE=4,所以AD=5,则DF=5.所以矩形BFDE的面积为5×4=20.
22.(1)EA
(2)证明:在矩形ABCD中,AD∥BC,∠A=90°,所以∠AEB=∠FBC.
因为CF⊥BE,所以∠CFB=∠A=90°.
由作图可知,BC=BE,所以△BFC≌△EAB,所以BF=EA.
23.(1)证明:因为EF∥BC,所以∠OEC=∠BCE.
因为CE平分∠ACB,所以∠BCE=∠OCE,所以∠OEC=∠OCE,所以EO=CO.
同理FO=CO,所以EO=FO.
(2)解:当点O运动到AC的中点时,四边形CEAF是矩形.
证明:由(1)得EO=FO.
因为O是AC的中点,所以AO=CO,所以四边形CEAF是平行四边形.
因为EO=FO=CO,所以EO=FO=AO=CO,即EF=AC,所以四边形CEAF是矩形.
(3)24 提示:由(2)得四边形CEAF是矩形,所以∠AEC=90°.
又AE=3,EC=4,所以AC=5,S△ACE =×3×4=6.
又因为AB=12,BC=13,所以122+52=132,所以△ABC是直角三角形,且∠BAC=90°.
所以S△ABC =×12×5=30,所以S四边形ABCE =S△ABC -S△ACE =30-6=24.
24.解:(1)四边形AEDF为平行四边形.理由如下:
因为DE∥AC,DF∥AB,所以四边形AEDF为平行四边形.
(2)当AD平分∠BAC时,四边形AEDF为菱形.理由如下:
因为DF∥AB,所以∠FDA=∠EAD.
因为AD平分∠BAC,所以∠FAD=∠EAD,所以∠FDA=∠FAD,所以AF=DF.
因为四边形AEDF为平行四边形,所以四边形AEDF为菱形.
(3)当△ABC满足∠CAB=90°时,四边形AEDF为正方形.
25.解:(1)能.理由如下:
在△DFC中,∠DFC=90°,∠C=30°,DC=4t,所以DF=2t.因为AE=2t,所以AE=DF.
因为AB⊥BC,DF⊥BC,所以AE∥DF.所以四边形AEFD为平行四边形.
当AE=AD时,四边形AEFD为菱形,即60-4t=2t,解得t=10.
所以当t=10 s时,四边形AEFD为菱形.
(2)①当∠DEF=90°时,由(1)知四边形AEFD为平行四边形,所以EF∥AD,
所以∠ADE=∠DEF=90°.
因为∠A=60°,所以∠AED=30°,所以AD=AE=t.
又AD=60-4t,即60-4t=t,解得t=12;
②当∠EDF=90°时,易得四边形EBFD为矩形.在Rt△AED中,∠A=60°,则∠ADE=30°,
所以AD=2AE,即60-4t=4t,解得t=.
③若∠EFD=90°,则E与B重合,D与A重合,此种情况不存在.
综上所述,当t=12 s或 s时,△DEF为直角三角形.
第3题图
第2题图
第1题图
第8题图
第7题图
第5题图
第10题图
第9题图
第13题图
第11题图
第12题图
(第13题图)
第14题图
第15题图
第16题图
第20题图
第21题图
第22题图
PAGE
1
