第三章变量之间的关系测试题(含答案)
文档属性
| 名称 | 第三章变量之间的关系测试题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 146.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-11 00:00:00 | ||
图片预览


文档简介
第三章变量之间的关系测试题(二)
(本试卷满分120分)
一、选择题(本大题共10小题,每小题3分,共30分)
1. 小明从广州给远在上海的爷爷打电话,电话费随着时间的变化而变化,在这个过程中,因变量是( )
A.小明 B.电话费 C.时间 D.爷爷
2. 北京时间2016年10月22日,广东省遭受台风“海马”袭击,大部分地区发生强降雨,某河受暴雨袭击,一天的水位记录如下表:
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
观察表中数据,水位上升最快的时段是( )
A.8~12时 B.12~16时 C.16~20时 D.20~24时
3. 笔记本每本a元,买3本笔记本共支出y元,支出y元随单价a元的变化而变化.在这个问题中,下列判断正确的是( )
A. a是常量,y是变量 B. a是变量,y是常量
C. a是变量,3也是变量 D. a,y都是变量
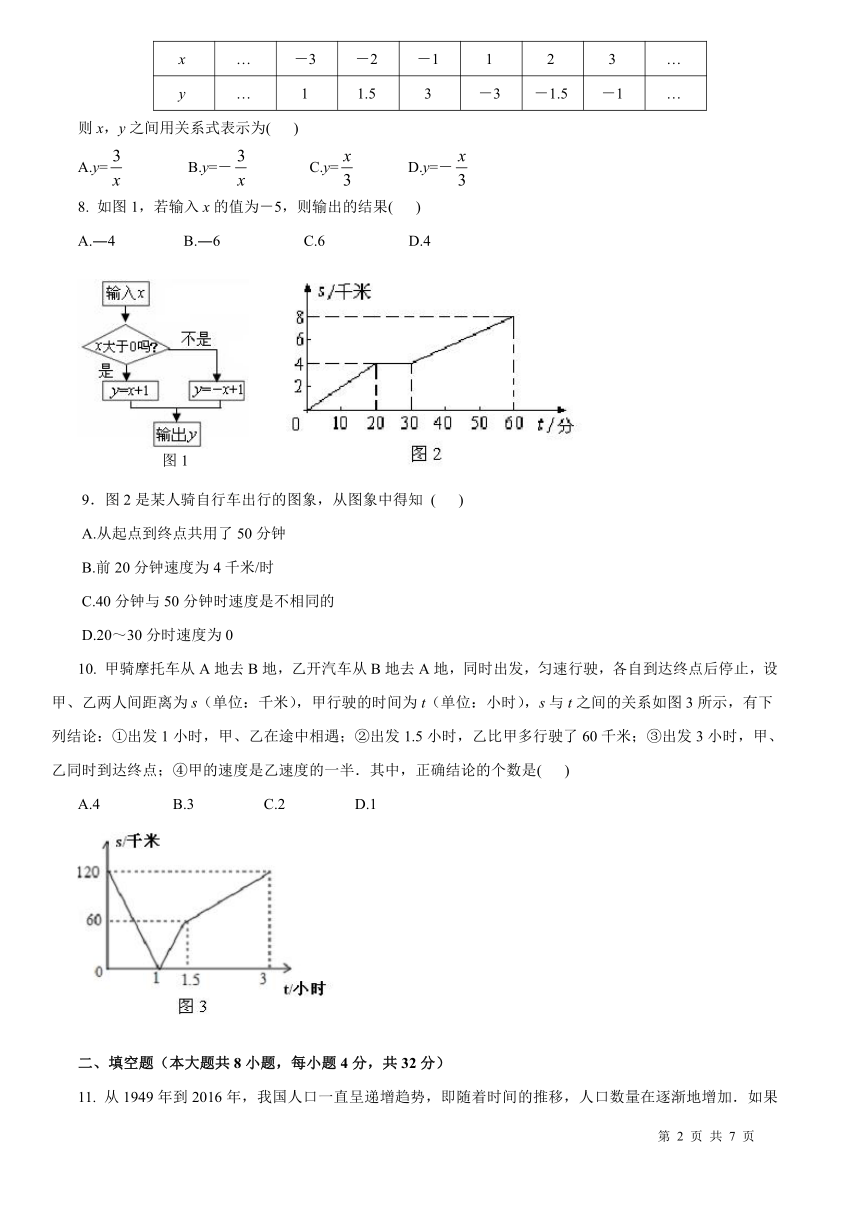
4. 同学们,你们喜欢打篮球吗?你还记得投篮时篮球出手后在空中飞行的路线吗?那就请你选一下,能反映出篮球的离地高度与投出后的时间之间关系的图象是( )
5. 一支铅笔是0.6元,小敏用5元买了x支铅笔,则余款y与x之间的关系式为( )
A.y=0.6x B.y=0.6x+5 C.y=5x-0.6 D.y=5-0.6x
6.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的关系用图象表示为 ( )
A B C D
7. 已知变量x,y满足下表的关系:
x … -3 -2 -1 1 2 3 …
y … 1 1.5 3 -3 -1.5 -1 …
则x,y之间用关系式表示为( )
A.y= B.y=- C.y= D.y=-
8. 如图1,若输入x的值为-5,则输出的结果( )
A.―4 B.―6 C.6 D.4
9.图2是某人骑自行车出行的图象,从图象中得知 ( )
A.从起点到终点共用了50分钟
B.前20分钟速度为4千米/时
C.40分钟与50分钟时速度是不相同的
D.20~30分时速度为0
10. 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的关系如图3所示,有下列结论:①出发1小时,甲、乙在途中相遇;②出发1.5小时,乙比甲多行驶了60千米;③出发3小时,甲、乙同时到达终点;④甲的速度是乙速度的一半.其中,正确结论的个数是( )
A.4 B.3 C.2 D.1
二、填空题(本大题共8小题,每小题4分,共32分)
11. 从1949年到2016年,我国人口一直呈递增趋势,即随着时间的推移,人口数量在逐渐地增加.如果用m表示时间,n表示人口数量,_________是自变量,________是因变量.
12. 表示两个变量之间的关系有三种方法,分别是__________、___________、___________.
13. 如图4,某埃博拉疑似病人夜里开始发烧, _______时烧得最厉害,医院及时抢救后体温开始下降,到_______时体温基本正常,但是_______时他的体温又升高了,直到夜里他才感觉到身上不那么烫.
14. 随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势:
年 份 2010 2011 2012 2013 …
入学儿童人数 2520 2330 2140 1950 …
上表中__________是自变量,__________是因变量;你预计该地区从__________年起入学儿童的人数不超过1000人.
15. 梯形上底长16,下底长x,高是10,梯形的面积S与下底长x间的关系式是___________.
16. 同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的关系式是y=x+32.如果某一温度的摄氏度数是25℃,那么它的华氏度数是________℉.
17. 如图5,圆柱的高是4厘米,当圆柱底面半径r(厘米)变化时,圆柱的体积V(立方厘米)也随之变化.
(1)圆柱的体积V与底面半径r的关系式是__________;
(2)当圆柱的底面半径由2变化到8时,圆柱的体积由________变化到________.(结果保留π)
18. 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图6的折线表示小强离开家的路程y(千米)和所用时间x(分)之间的关系.下列有四种说法:①小强从家到公共汽车站步行了2千米;②小强在公共汽车站等小明用了10分钟;③公共汽车的平均速度是30千米/时;④小强乘公共汽车用了20分钟.其中正确的是__________.
三、解答题(本大题共5小题,共58分)
19.(10分)1766年德国人提丢斯发现,太阳系中的行星到太阳的距离遵循一定的规律,如下表所示:
颗 次 1 2 3 4 5 6 …
行星名称 水星 金星 地球 火星 小行星 木星 …
距离(天文单位) 0.4 0.7 1 1.6 2.8 5.2 …
0.4 0.4+0.3 0.4+0.6 0.4+1.2 0.4+2.4 … …
那么第7颗行星到太阳的距离是多少天文单位?
20.(10分)声音在空气中的传播速度v(米/秒)与温度t(oC)的关系可表示为v=331+0.6t.当t的值分别是-1,0,3,10,25时,计算相应的v的值,并用表格表示所得结果.
21.(12分)一辆汽车行驶中速度随时间变化的图象如图7所示,请说明汽车的行驶状态.
22.(12分)小亮帮母亲预算家庭4月份电费开支情况,下表是小亮家4月初连续8天每天早上电表显示的读数.
日期 1 2 3 4 5 6 7 8
电表读数 21 24 27 30 33 36 39 42
(1)表格中反映的变量是______,自变量是______,因变量是______.
(2)估计小亮家4月份的用电量是多少度.若每度电电费是0.49元,估计他家4月份应交的电费是多少元.
23.(14分)如图8,三角形底边长为8 cm,当它的高由小到大变化时,三角形的面积也随之发生了变化.
(1)在这个变化过程中,自变量和因变量分别是什么?
(2)如果三角形的高为h cm,写出三角形的面积S与高h的关系式.
(3)当高由1 cm变化到5 cm时,面积从_________cm2变化到_________cm2.
附加题(15分,不计入总分)
24.已知动点P以每秒2 cm的速度沿图9甲所示的边框按B→C→D→E→F→A的路径移动,相应的三角形ABP的面积S关于时间t的图象如图9乙所示,若AB=6cm,试回答下列问题:
(1)如图甲,BC的长是多少?图形面积是多少?
(2)如图乙,图中的a是多少?b是多少?
(河北 马小宇)
第三章变量之间的关系测试题(二)参考答案
一、1.B 2.D 3.D 4.C 5.D 6.D 7.B 8.C 9.D
10.B 提示:(1)由图象可得A,B两地相距120千米,出发1小时,甲、乙在途中相遇(即甲、乙两人间距离为0),故①正确;
(2)甲骑摩托车的速度为120÷3=40(千米/时),设乙开汽车的速度为a千米/时,则(40+a)×1=120,解得a=80,所以乙开汽车的速度为80千米/时,所以甲的速度是乙速度的一半,故④正确;
(3)出发1.5小时,乙比甲多行驶了1.5×(80-40)=60(千米),故②正确;
(4)乙到达终点所用的时间为120÷80=1.5(小时),甲到达终点所用的时间为3小时,故③错误.
所以正确的有3个.
二、11. m n 12. 表格法 关系式法 图象法 13.6 12 18
14. 年份 入学儿童人数 2018 15. S=80+5x 16. 77 17. (1)V=4πr2 (2)16π 256π
18. ①②③
提示:通过图象观察出来,当第一段图象结束时,纵轴上的数为2,显示小强这一段走了2千米,故①正确;第二段时间从20分钟变化到30分钟,y没有改变,所以这一段时间内小强都在等小明,等了10分钟,故②正确;第三段时间是从30分钟到60分钟,路程变化从2千米到17千米,所以公共汽车的速度是(17-2)÷[(60-30)÷60]=30(千米/时),故③正确;第三段时间是从30分钟到60分钟,可以看出小强乘公共汽车用了30分钟,而不是20分钟,故④错误.
三、19.解:通过观察表格,行星的颗次依次增加,行星到太阳的距离也依次增加,由规律可得第6颗行星到太阳的距离是0.4+2.4×2=5.2(天文单位);第7颗行星到太阳的距离是0.4+4.8×2=10(天文单位).所以第7颗行星到太阳的距离是10天文单位.
20. 解:相应的v值用表格表示为:
t/oC -1 0 3 10 25
v/(米/秒) 330.4 331 332.8 337 346
21.解:汽车先加速行驶一段时间,然后匀速行驶一段时间后,开始减速行驶,到停止,又加速行驶.
22. 解:(1)日期和电表读数 日期 电表读数
(2)每天的用电量是3度,4月份的用电量=30×3=90(度).
因为每度电的电费是0.49元,所以4月份应交的电费是90×0.49=44.1(元).
所以估计小亮家4月份的用电量是90度,应交的电费是44.1元.
23.(1)自变量是三角形的高,因变量是三角形的面积;
(2)S=4h;
(3)4 20
24.解:(1)如图甲,当点P在BC上时,以AB为底的三角形ABP的高在不断增大,到达点C时,开始不变,由图乙得点P在BC上移动了4秒,则BC=4×2=8(cm);在CD上移动了2秒,则CD=2×2=4(cm),在DE上移动了3秒,则DE=3×2=6(cm;而AB=6cm,那么EF=AB-CD=6-4=2(cm),需要移动2÷2=1(秒);AF=BC+DE=8+6=14(cm),需要移动14÷2=7(秒).所以S图形=AB×BC+DE×EF=6×8+6×2=60(cm2).
所以BC长是8 cm,图形的面积是60 cm2.
(2)由图乙得a是点P运行4秒时三角形ABP的面积,因为S三角形ABP=×6×8=24,所以a的值为24.
b为点P走完全程的时间,为t=9+1+7=17(秒).
所以a的值是24,b的值是17.
A B C D
图1
图5
图7
图8
PAGE
第 5 页 共 7 页
(本试卷满分120分)
一、选择题(本大题共10小题,每小题3分,共30分)
1. 小明从广州给远在上海的爷爷打电话,电话费随着时间的变化而变化,在这个过程中,因变量是( )
A.小明 B.电话费 C.时间 D.爷爷
2. 北京时间2016年10月22日,广东省遭受台风“海马”袭击,大部分地区发生强降雨,某河受暴雨袭击,一天的水位记录如下表:
时间/时 0 4 8 12 16 20 24
水位/米 2 2.5 3 4 5 6 8
观察表中数据,水位上升最快的时段是( )
A.8~12时 B.12~16时 C.16~20时 D.20~24时
3. 笔记本每本a元,买3本笔记本共支出y元,支出y元随单价a元的变化而变化.在这个问题中,下列判断正确的是( )
A. a是常量,y是变量 B. a是变量,y是常量
C. a是变量,3也是变量 D. a,y都是变量
4. 同学们,你们喜欢打篮球吗?你还记得投篮时篮球出手后在空中飞行的路线吗?那就请你选一下,能反映出篮球的离地高度与投出后的时间之间关系的图象是( )
5. 一支铅笔是0.6元,小敏用5元买了x支铅笔,则余款y与x之间的关系式为( )
A.y=0.6x B.y=0.6x+5 C.y=5x-0.6 D.y=5-0.6x
6.汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的关系用图象表示为 ( )
A B C D
7. 已知变量x,y满足下表的关系:
x … -3 -2 -1 1 2 3 …
y … 1 1.5 3 -3 -1.5 -1 …
则x,y之间用关系式表示为( )
A.y= B.y=- C.y= D.y=-
8. 如图1,若输入x的值为-5,则输出的结果( )
A.―4 B.―6 C.6 D.4
9.图2是某人骑自行车出行的图象,从图象中得知 ( )
A.从起点到终点共用了50分钟
B.前20分钟速度为4千米/时
C.40分钟与50分钟时速度是不相同的
D.20~30分时速度为0
10. 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的关系如图3所示,有下列结论:①出发1小时,甲、乙在途中相遇;②出发1.5小时,乙比甲多行驶了60千米;③出发3小时,甲、乙同时到达终点;④甲的速度是乙速度的一半.其中,正确结论的个数是( )
A.4 B.3 C.2 D.1
二、填空题(本大题共8小题,每小题4分,共32分)
11. 从1949年到2016年,我国人口一直呈递增趋势,即随着时间的推移,人口数量在逐渐地增加.如果用m表示时间,n表示人口数量,_________是自变量,________是因变量.
12. 表示两个变量之间的关系有三种方法,分别是__________、___________、___________.
13. 如图4,某埃博拉疑似病人夜里开始发烧, _______时烧得最厉害,医院及时抢救后体温开始下降,到_______时体温基本正常,但是_______时他的体温又升高了,直到夜里他才感觉到身上不那么烫.
14. 随着我国人口增长速度的减慢,小学入学儿童数量有所减少.下表中的数据近似地呈现了某地区入学儿童人数的变化趋势:
年 份 2010 2011 2012 2013 …
入学儿童人数 2520 2330 2140 1950 …
上表中__________是自变量,__________是因变量;你预计该地区从__________年起入学儿童的人数不超过1000人.
15. 梯形上底长16,下底长x,高是10,梯形的面积S与下底长x间的关系式是___________.
16. 同一温度的华氏度数y(℉)与摄氏度数x(℃)之间的关系式是y=x+32.如果某一温度的摄氏度数是25℃,那么它的华氏度数是________℉.
17. 如图5,圆柱的高是4厘米,当圆柱底面半径r(厘米)变化时,圆柱的体积V(立方厘米)也随之变化.
(1)圆柱的体积V与底面半径r的关系式是__________;
(2)当圆柱的底面半径由2变化到8时,圆柱的体积由________变化到________.(结果保留π)
18. 某星期天下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图6的折线表示小强离开家的路程y(千米)和所用时间x(分)之间的关系.下列有四种说法:①小强从家到公共汽车站步行了2千米;②小强在公共汽车站等小明用了10分钟;③公共汽车的平均速度是30千米/时;④小强乘公共汽车用了20分钟.其中正确的是__________.
三、解答题(本大题共5小题,共58分)
19.(10分)1766年德国人提丢斯发现,太阳系中的行星到太阳的距离遵循一定的规律,如下表所示:
颗 次 1 2 3 4 5 6 …
行星名称 水星 金星 地球 火星 小行星 木星 …
距离(天文单位) 0.4 0.7 1 1.6 2.8 5.2 …
0.4 0.4+0.3 0.4+0.6 0.4+1.2 0.4+2.4 … …
那么第7颗行星到太阳的距离是多少天文单位?
20.(10分)声音在空气中的传播速度v(米/秒)与温度t(oC)的关系可表示为v=331+0.6t.当t的值分别是-1,0,3,10,25时,计算相应的v的值,并用表格表示所得结果.
21.(12分)一辆汽车行驶中速度随时间变化的图象如图7所示,请说明汽车的行驶状态.
22.(12分)小亮帮母亲预算家庭4月份电费开支情况,下表是小亮家4月初连续8天每天早上电表显示的读数.
日期 1 2 3 4 5 6 7 8
电表读数 21 24 27 30 33 36 39 42
(1)表格中反映的变量是______,自变量是______,因变量是______.
(2)估计小亮家4月份的用电量是多少度.若每度电电费是0.49元,估计他家4月份应交的电费是多少元.
23.(14分)如图8,三角形底边长为8 cm,当它的高由小到大变化时,三角形的面积也随之发生了变化.
(1)在这个变化过程中,自变量和因变量分别是什么?
(2)如果三角形的高为h cm,写出三角形的面积S与高h的关系式.
(3)当高由1 cm变化到5 cm时,面积从_________cm2变化到_________cm2.
附加题(15分,不计入总分)
24.已知动点P以每秒2 cm的速度沿图9甲所示的边框按B→C→D→E→F→A的路径移动,相应的三角形ABP的面积S关于时间t的图象如图9乙所示,若AB=6cm,试回答下列问题:
(1)如图甲,BC的长是多少?图形面积是多少?
(2)如图乙,图中的a是多少?b是多少?
(河北 马小宇)
第三章变量之间的关系测试题(二)参考答案
一、1.B 2.D 3.D 4.C 5.D 6.D 7.B 8.C 9.D
10.B 提示:(1)由图象可得A,B两地相距120千米,出发1小时,甲、乙在途中相遇(即甲、乙两人间距离为0),故①正确;
(2)甲骑摩托车的速度为120÷3=40(千米/时),设乙开汽车的速度为a千米/时,则(40+a)×1=120,解得a=80,所以乙开汽车的速度为80千米/时,所以甲的速度是乙速度的一半,故④正确;
(3)出发1.5小时,乙比甲多行驶了1.5×(80-40)=60(千米),故②正确;
(4)乙到达终点所用的时间为120÷80=1.5(小时),甲到达终点所用的时间为3小时,故③错误.
所以正确的有3个.
二、11. m n 12. 表格法 关系式法 图象法 13.6 12 18
14. 年份 入学儿童人数 2018 15. S=80+5x 16. 77 17. (1)V=4πr2 (2)16π 256π
18. ①②③
提示:通过图象观察出来,当第一段图象结束时,纵轴上的数为2,显示小强这一段走了2千米,故①正确;第二段时间从20分钟变化到30分钟,y没有改变,所以这一段时间内小强都在等小明,等了10分钟,故②正确;第三段时间是从30分钟到60分钟,路程变化从2千米到17千米,所以公共汽车的速度是(17-2)÷[(60-30)÷60]=30(千米/时),故③正确;第三段时间是从30分钟到60分钟,可以看出小强乘公共汽车用了30分钟,而不是20分钟,故④错误.
三、19.解:通过观察表格,行星的颗次依次增加,行星到太阳的距离也依次增加,由规律可得第6颗行星到太阳的距离是0.4+2.4×2=5.2(天文单位);第7颗行星到太阳的距离是0.4+4.8×2=10(天文单位).所以第7颗行星到太阳的距离是10天文单位.
20. 解:相应的v值用表格表示为:
t/oC -1 0 3 10 25
v/(米/秒) 330.4 331 332.8 337 346
21.解:汽车先加速行驶一段时间,然后匀速行驶一段时间后,开始减速行驶,到停止,又加速行驶.
22. 解:(1)日期和电表读数 日期 电表读数
(2)每天的用电量是3度,4月份的用电量=30×3=90(度).
因为每度电的电费是0.49元,所以4月份应交的电费是90×0.49=44.1(元).
所以估计小亮家4月份的用电量是90度,应交的电费是44.1元.
23.(1)自变量是三角形的高,因变量是三角形的面积;
(2)S=4h;
(3)4 20
24.解:(1)如图甲,当点P在BC上时,以AB为底的三角形ABP的高在不断增大,到达点C时,开始不变,由图乙得点P在BC上移动了4秒,则BC=4×2=8(cm);在CD上移动了2秒,则CD=2×2=4(cm),在DE上移动了3秒,则DE=3×2=6(cm;而AB=6cm,那么EF=AB-CD=6-4=2(cm),需要移动2÷2=1(秒);AF=BC+DE=8+6=14(cm),需要移动14÷2=7(秒).所以S图形=AB×BC+DE×EF=6×8+6×2=60(cm2).
所以BC长是8 cm,图形的面积是60 cm2.
(2)由图乙得a是点P运行4秒时三角形ABP的面积,因为S三角形ABP=×6×8=24,所以a的值为24.
b为点P走完全程的时间,为t=9+1+7=17(秒).
所以a的值是24,b的值是17.
A B C D
图1
图5
图7
图8
PAGE
第 5 页 共 7 页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
