第2章 四边形测试题（含答案）

第2章 四边形测试题（一）
一、选择题（每小题3分，共30分）
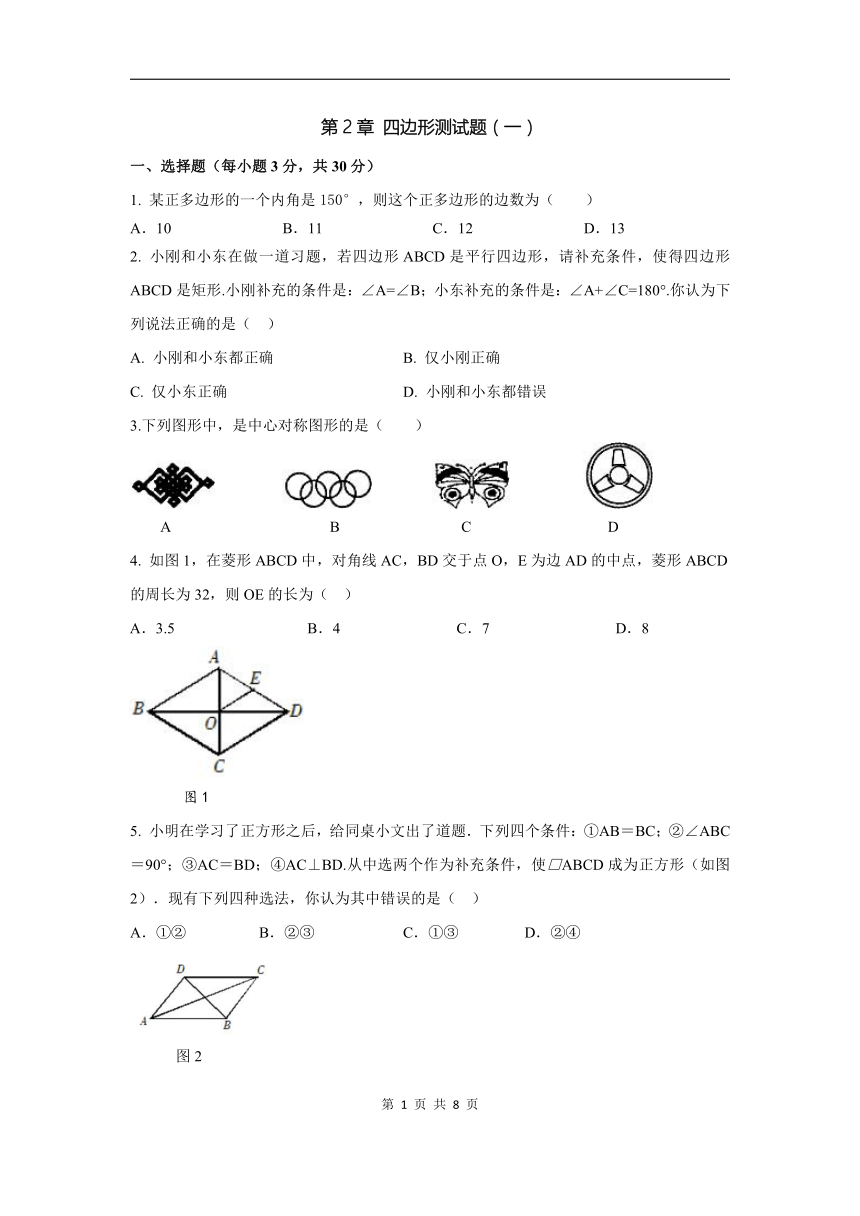
1. 某正多边形的一个内角是150°，则这个正多边形的边数为（　　）
A．10 B．11 C．12 D．13
2. 小刚和小东在做一道习题，若四边形ABCD是平行四边形，请补充条件，使得四边形ABCD是矩形.小刚补充的条件是：∠A=∠B；小东补充的条件是：∠A+∠C=180°.你认为下列说法正确的是（ ）
A. 小刚和小东都正确 B. 仅小刚正确
C. 仅小东正确 D. 小刚和小东都错误
3.下列图形中，是中心对称图形的是（　　）

A B C D
4. 如图1，在菱形ABCD中，对角线AC，BD交于点O，E为边AD的中点，菱形ABCD的周长为32，则OE的长为（ ）
A．3.5 B．4 C．7 D．8

图1
5. 小明在学习了正方形之后，给同桌小文出了道题．下列四个条件：①AB＝BC；②∠ABC＝90°；③AC＝BD；④AC⊥BD.从中选两个作为补充条件，使□ABCD成为正方形（如图2）．现有下列四种选法，你认为其中错误的是（ ）
A．①② B．②③ C．①③ D．②④

图2
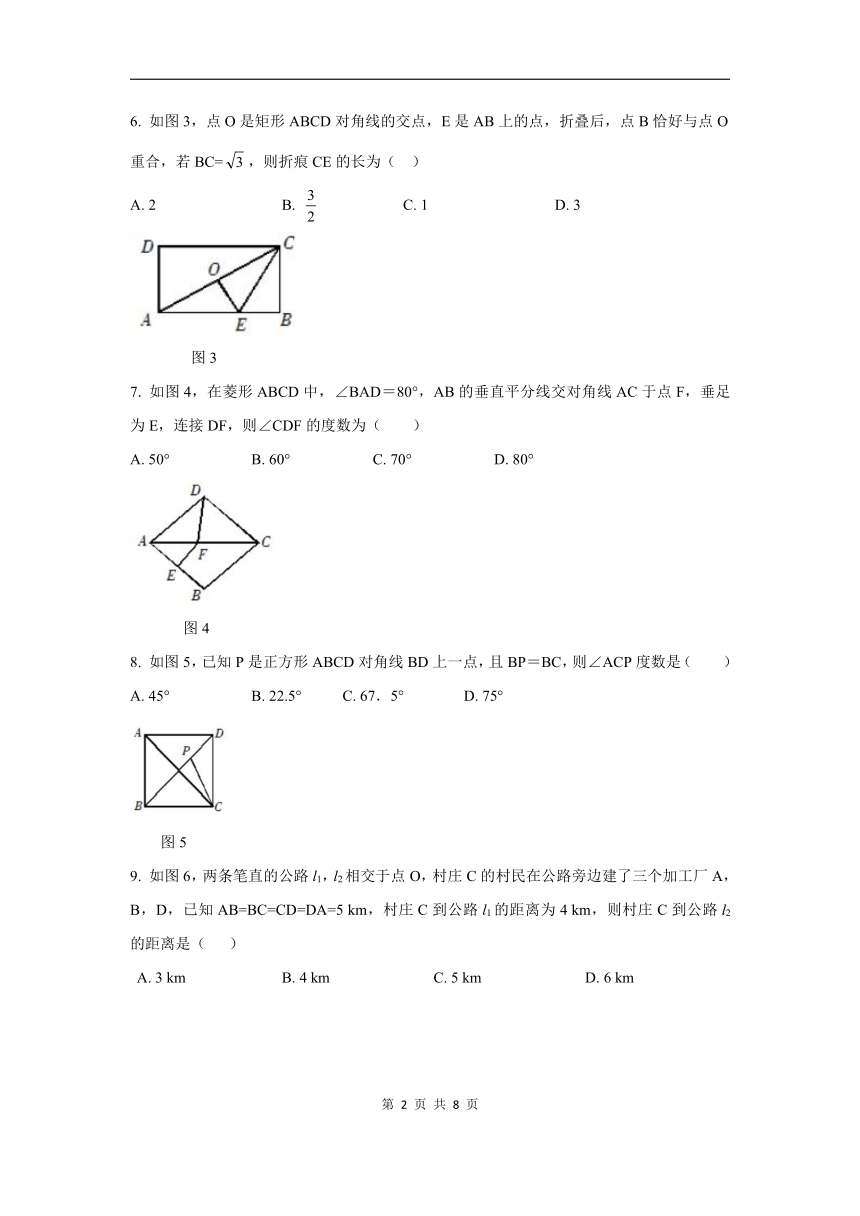
6. 如图3，点O是矩形ABCD对角线的交点，E是AB上的点，折叠后，点B恰好与点O重合，若BC=，则折痕CE的长为（ ）
A. 2 B. C. 1 D. 3

图3
7. 如图4，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CDF的度数为（　　）
A. 50° B. 60° C. 70° D. 80°

图4
8. 如图5，已知P是正方形ABCD对角线BD上一点，且BP＝BC，则∠ACP度数是（　　）
A. 45° B. 22.5° C. 67．5° D. 75°

图5
9. 如图6，两条笔直的公路l1，l2相交于点O，村庄C的村民在公路旁边建了三个加工厂A，B，D，已知AB=BC=CD=DA=5 km，村庄C到公路l1的距离为4 km，则村庄C到公路l2的距离是（ ）
A. 3 km B. 4 km C. 5 km D. 6 km

图6
10. 如图7，过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE，CF．若AB=，∠DCF=30°，则EF的长为（　　）
A. 2 B. 3 C. D.

图7
二、填空题（每小题4分，共32分）
11. 如图8所示，四边形ABCD是菱形，对角线AC，BD相交于点O，AC=4 cm，BD=8 cm，则这个菱形的面积是___________cm2．

图8
12. 若过多边形的每一个顶点有6条对角线，则这个多边形是 边形．
13. 如图9，矩形ABCD的对角线AC，BD相交于点O，AB=2，∠AOB=60°，则对角线AC的长为___________．

图9
14. 如10图所示，在正方形ABCD中，如果AF=BE，那么∠AOD的度数是 ．

图10
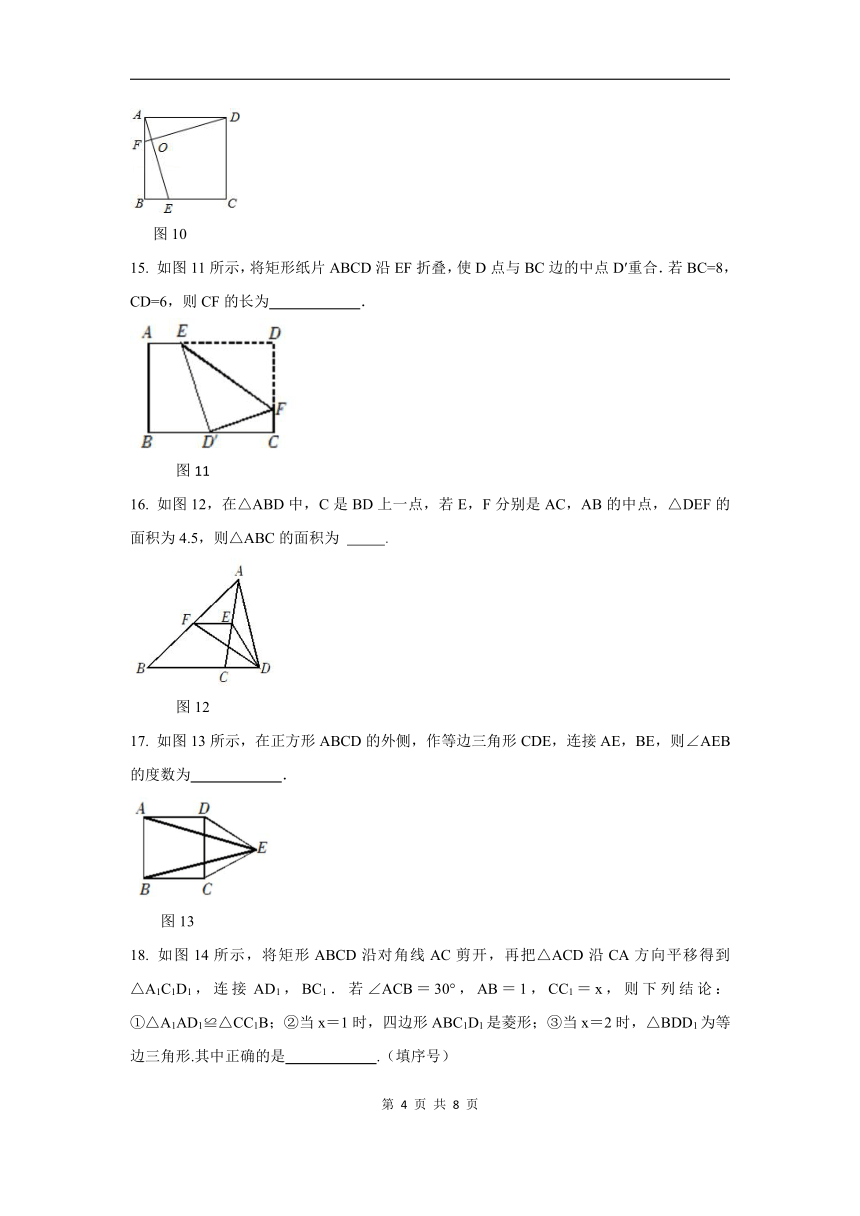
15. 如图11所示，将矩形纸片ABCD沿EF折叠，使D点与BC边的中点D′重合．若BC=8，CD=6，则CF的长为 ．

图11
16. 如图12，在△ABD中，C是BD上一点，若E，F分别是AC，AB的中点，△DEF的面积为4.5，则△ABC的面积为 ．

图12
17. 如图13所示，在正方形ABCD的外侧，作等边三角形CDE，连接AE，BE，则∠AEB的度数为 ．

图13
18. 如图14所示，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1，连接AD1，BC1．若∠ACB＝30°，AB＝1，CC1＝x，则下列结论：①△A1AD1≌△CC1B；②当x＝1时，四边形ABC1D1是菱形；③当x＝2时，△BDD1为等边三角形.其中正确的是 .（填序号）

图 14
三、解答题（共58分）
19.（8分）如图15，四边形ABCD是矩形，E是AB上一点，且DE＝AB，过点C作CF⊥DE于点F．
（1）猜想AD与CF的大小关系；
（2）请证明上面的结论．

图15
20. (8分) 一个多边形的内角和比外角和的4倍多180°，求这个多边形的边数及内角和．

21.（10分）如图16所示，AC是□ABCD的一条对角线，过AC中点O的直线分别交AD，BC于点E，F.
（1）求证：△AOE≌△COF；
（2）当EF与AC满足什么条件时，四边形AFCE是菱形？并说明理由.

图16

22.（10分）如图17所示，矩形ABCD的对角线AC，BD相交于点O，DE∥CA，AE∥BD．
（1）求证：四边形AODE是菱形；
（2）若将题设中“矩形ABCD”这一条件改为“菱形ABCD”，其余条件不变，则四边形AODE是矩形吗？为什么？

．图17
23.（10分）在一张长12 cm、宽5 cm的长方形纸片内，要折出一个菱形.小颖同学按照取两组对边中点的方法折出菱形EFGH（如图18-①），小明同学沿长方形的对角线AC折出∠CAE＝∠CAD，∠ACF＝∠ACB的方法得到菱形AECF（如图18-②）.请问小颖和小明同学的折法中，哪个菱形面积较大？

图18
24.（12分）如图19-①，在正方形ABCD中，E，F分别是边AD，DC上的点，且AF⊥BE．
（1）求证：AF=BE；
（2）如图19-②，在正方形ABCD中，M，N，P，Q分别是边AB，BC，CD，DA上的点，且MP⊥NQ，那么MP与NQ是否相等？并说明理由．

图19












第2章 四边形测试题（一）参考答案
一、1. C 2. A 3. A 4. B 5. B 6. A 7. B 8. B 9. B 10. A
二、11.16 12. 九 13. 4 14. 90° 15. 16. 18 17. 30° 18. ①②③
三、19 .解：（1）AD＝CF．
（2）因为四边形ABCD是矩形，所以AB∥DC.
所以∠AED＝∠FDC，AB＝CD.
又DE＝AB，所以DE＝CD.
因为CF⊥DE，所以∠CFD＝∠A＝90°．
所以△ADE≌△FCD.所以AD＝CF．
20. 解：设该多边形的边数为n，根据题意，得（n-2）?180=360×4+180.
解得n=11．
（11-2）×180°=1620°.
答：这个多边形的边数是11，内角和是1620°.
21.证明：（1）因为四边形ABCD是平行四边形，
所以AD∥BC.所以∠EAO=∠FCO.
因为O是AC的中点，所以AO=CO.
又∠EOA=∠FOC，所以△AOE≌△COF.
（2）当EF⊥AC时，四边形AFCE是菱形.
理由：由（1）知△AOE≌△COF，所以OE=OF.
又AO=CO，所以四边形AFCE是平行四边形.
所以当EF⊥AC时，平行四边形AFCE是菱形.
22 .证明：（1）因为DE∥CA，AE∥BD，
所以四边形AODE是平行四边形.
因为四边形ABCD是矩形，
所以OA=OC，OD=OB，AC=BD.所以OA=OD.
所以平行四边形AODE是菱形．
（2）四边形AODE是矩形.
理由：因为DE∥CA，AE∥BD，
所以四边形AODE是平行四边形.
因为四边形ABCD是菱形，
所以AC⊥BD，即∠AOD=90°.
所以平行四边形AODE是矩形.
23.解：小颖的折法：S菱形EFGH＝×12×5＝30（cm2）；
小明的折法：设BE＝x cm，则AE＝CE=（12－x）cm.
在Rt△ABE中，由勾股定理，得（12－x）2＝52+x2，
解得x＝，则EC＝.
所以S菱形AECF＝×5＝（cm2）.
因为30<，所以小明折出的菱形面积较大.
24.证明:（1）在正方形ABCD中，AB=AD，∠BAE=∠D=90°.
所以∠DAF+∠BAF=90°.
因为AF⊥BE，所以∠ABE+∠BAF=90°.
所以∠ABE=∠DAF.
所以△ABE≌△DAF.所以AF=BE.
（2）MP=NQ．
理由：过点A作AF∥MP交CD于点F，过点B作BE∥NQ交AD于点E，则与（1）的情况完全相同，可得AF=BE，从而MP=NQ.





第 1 页 共 8 页