湘教版2018-2019学年度下学期八年级数学期中测试题(含答案)
文档属性
| 名称 | 湘教版2018-2019学年度下学期八年级数学期中测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 178.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-11 13:07:24 | ||
图片预览

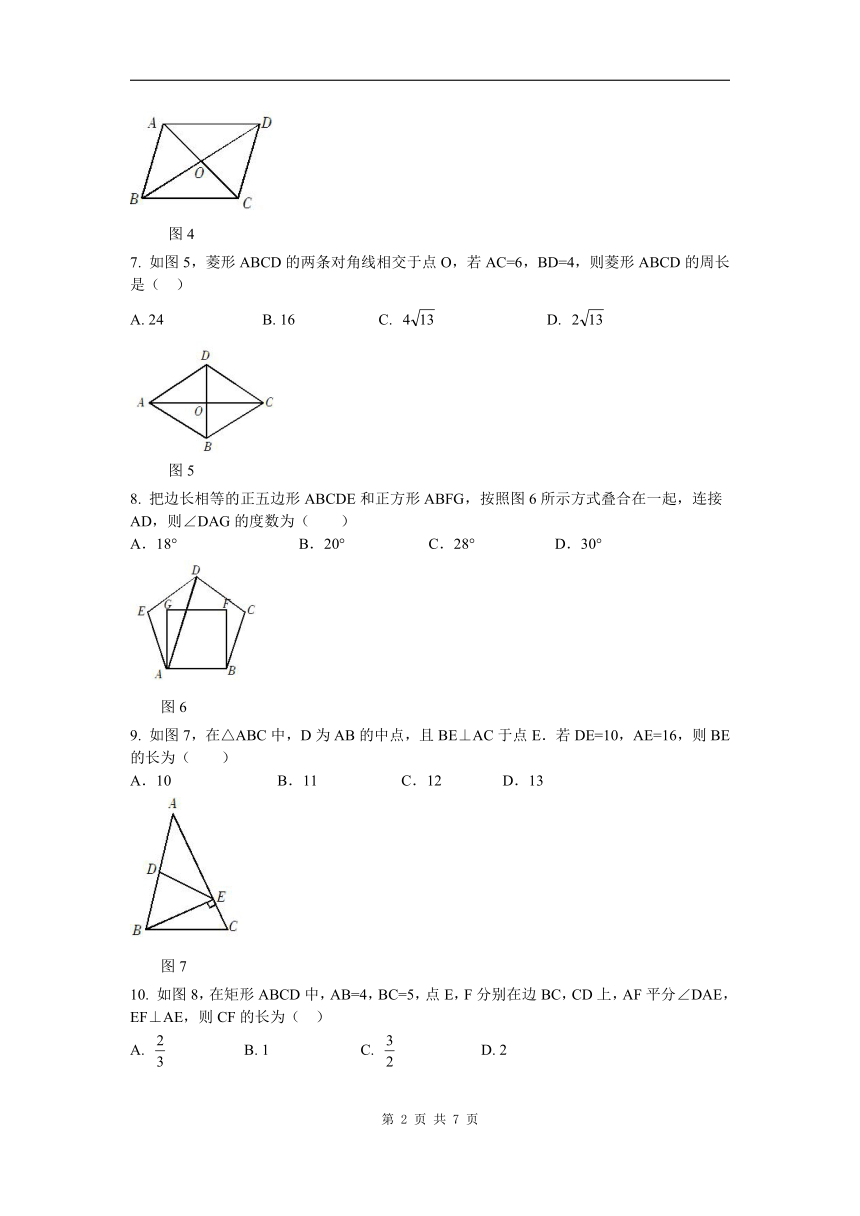
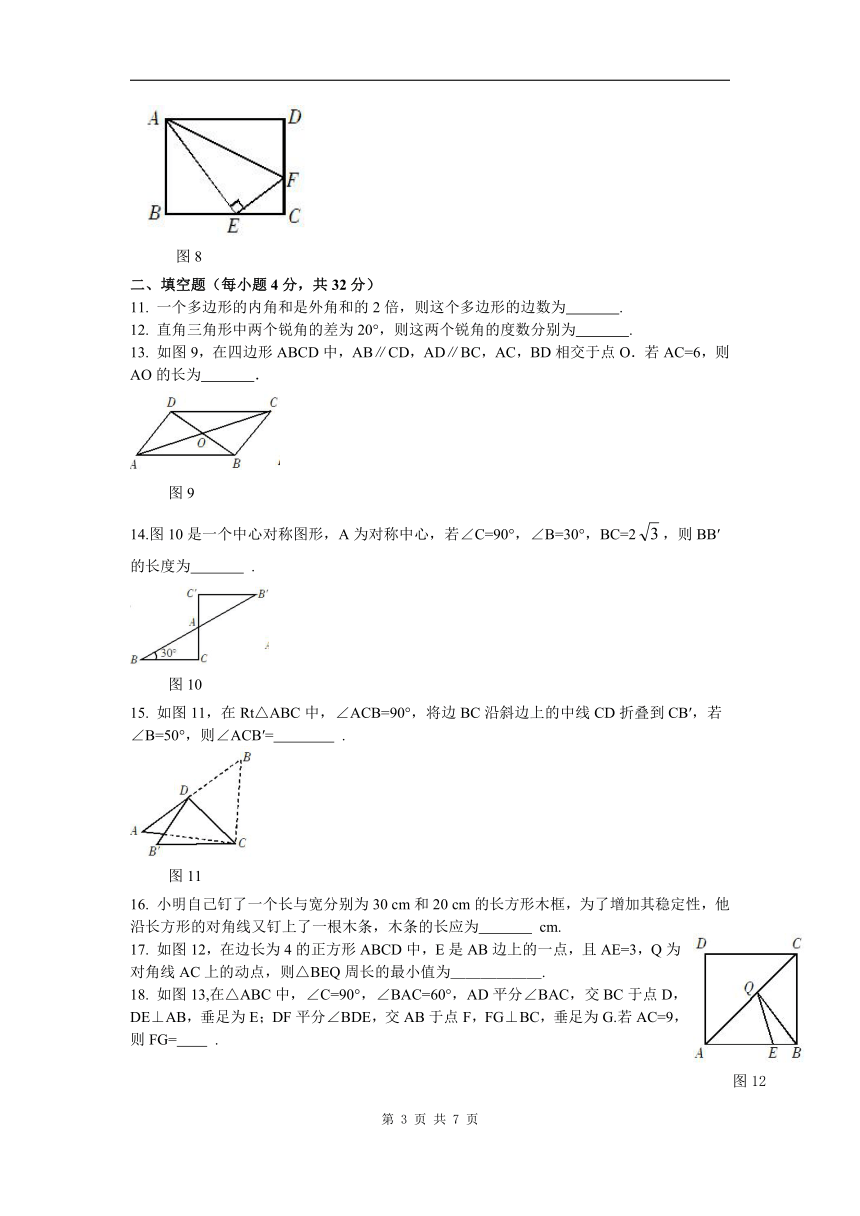
文档简介
期中测试题
一、选择题(每小题3分,共30分)
1. 下列生态环保标志中,是中心对称图形的是( )
A B C D
2. 下列四组线段中,可以构成直角三角形的是( )
A. 4,5,6 B. 1.5,2,2.5 C. 2,3,4 D. 1,,3
3. 如图1,a∥b,若要△ABC的面积与△DEF的面积相等,需增加条件( )
A. AB=DF B. AC=DE C. BC=EF D. BE=AD
图1
4. 如图2,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )
A.图中有三个直角三角形 B.∠1=∠2
C.∠1和∠B都是∠A的余角 D.∠2=∠A
图2
5. 如图3,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF B. ∠A=∠D C. ∠B=∠C D. AB=DC
图3
6. 如图4,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件可以是( )
A.AB=CD B. AD=BC C.AB=BC D.AC=BD
图4
7. 如图5,菱形ABCD的两条对角线相交于点O,若AC=6,BD=4,则菱形ABCD的周长是( )
A. 24 B. 16 C. D.
图5
8. 把边长相等的正五边形ABCDE和正方形ABFG,按照图6所示方式叠合在一起,连接AD,则∠DAG的度数为( )
A.18° B.20° C.28° D.30°
图6
9. 如图7,在△ABC中,D为AB的中点,且BE⊥AC于点E.若DE=10,AE=16,则BE的长为( )
A.10 B.11 C.12 D.13
图7
10. 如图8,在矩形ABCD中,AB=4,BC=5,点E,F分别在边BC,CD上,AF平分∠DAE,EF⊥AE,则CF的长为( )
A. B. 1 C. D. 2
图8
二、填空题(每小题4分,共32分)
11. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .
12. 直角三角形中两个锐角的差为20°,则这两个锐角的度数分别为 .
13. 如图9,在四边形ABCD中,AB∥CD,AD∥BC,AC,BD相交于点O.若AC=6,则AO的长为 .
图9
14.图10是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,BC=2,则BB′的长度为 .
图10
15. 如图11,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=50°,则∠ACB′= .
图11
16. 小明自己钉了一个长与宽分别为30 cm和20 cm的长方形木框,为了增加其稳定性,他沿长方形的对角线又钉上了一根木条,木条的长应为 cm.
17. 如图12,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,Q为对角线AC上的动点,则△BEQ周长的最小值为______.
18. 如图13,在△ABC中,∠C=90°,∠BAC=60°,AD平分∠BAC,交BC于点D,DE⊥AB,垂足为E;DF平分∠BDE,交AB于点F,FG⊥BC,垂足为G.若AC=9,则FG= .
图13
三、解答题(共58分)
19. (6分)在城市广场上,有一种多边形地砖的内角和为540°,请你求出这种多边形地砖的边数.
20. (6分))如图14,正方形网格中每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点按下列要求画三角形:使三角形的三边长分别为3,,.
图14
21.(8分)如图15,已知E,F分别是?ABCD的边AB,CD上的点,AE=CF,DE,AF交于点G,CE,BF交于点H.求证:四边形EHFG是平行四边形.
图15
22. (8分)如图16,小红同学要测量A,C两地之间的距离,但A,C之间有一水池,不能直接测量,于是她在A,C同一水平面上选取了一点B,点B可直接到达A,C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A,C两地之间的距离.(参考数据:≈4.6)
图16
23.(8分)如图17,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
图17
24. (10分)如图18,在Rt△ABC中,BD是中线,分别过点A,B作AE∥BD,BE∥AC.
(1)试判断四边形AEBD的形状,并说明理由;
(2)连接EC,交BD于点F,求证:EC平分BD.
图18
25. (12分)如图19,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)若D为AB的中点,四边形BECD是什么特殊四边形?请说明理由;
(3)若D为AB的中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明理由.
图19
期中测试题参考答案
一、1. B 2. B 3. C 4. B 5. D 6. D 7.C 8. A 9. C 10. C
二、11. 6 12. 35°,55° 13.3 14.8 15.10° 16. 17. 6 18.3
三、19. 解:设这种多边形地砖的边数为n.
根据题意,得(n-2)·180=540,解得n=5.
所以这种多边形地砖的边数为5.
20.解:答案不唯一,给出一种如图1所示:
图1
21. 证明:因为四边形ABCD是平行四边形,所以AB∥CD,AB=CD.
又AE=CF,所以EB=DF.
所以四边形AECF,DEBF是平行四边形.
所以AF∥CE,DE∥FB.
所以四边形EHFG是平行四边形
22. 解:如图2,过点C作CD⊥AB交AB的延长线于点D .
因为∠ABC=120°,所以∠CBD=60°.
在Rt△BCD中,∠BCD=90°-∠CBD=30°,所以BD=BC=×20=10(米).
所以CD===10(米),AD=AB+BD=80+10=90(米).
在Rt△ACD中,根据勾股定理,得AC===20≈92(米).
所以A,C两地之间的距离约为92米.
图2
23.(1)证明:因为四边形ABCD是正方形,所以BC=CD,∠B=∠CDF=90°.
又BE=DF,所以△CBE≌△CDF.所以CE=CF.
(2)解:GE=BE+GD成立.
理由:由(1)知△CBE≌△CDF,所以∠BCE=∠DCF.
所以∠DCF+∠ECD=∠BCE+∠ECD,即∠ECF=∠BCD=90°.
又∠GCE=45°,所以∠GCF=∠GCE=45°.
在△ECG和△FCG中,CE=CF,∠GCE=∠GCF,GC=GC,所以△ECG≌△FCG
所以GE=GF=DF+GD=BE+GD.
24.(1)解:四边形AEBD是菱形.
理由:因为AE∥BD,BE∥AC,所以四边形AEBD是平行四边形.
在Rt△ABC中,BD是中线,所以BD=AD=AC.
所以?AEBD是菱形.
(2)证明:连接DE.
由(1)知四边形AEBD是菱形,则BE=BD.
又BD=DC,所以BE=DC.
又BE∥DC,所以四边形BCDE是平行四边形.
所以EC平分BD.
25. (1)证明:因为DE⊥BC,所以∠DFB=90°.
因为∠ACB=90°,所以∠ACB=∠DFB. 所以AC∥DE.
因为MN∥AB,即CE∥AD,所以四边形ADEC是平行四边形.所以CE=AD.
(2)解:四边形BECD是菱形.
理由:因为D为AB的中点,所以AD=BD.
因为CE=AD,所以BD=CE.
又BD∥CE,所以四边形BECD是平行四边形.
又DE⊥BC,所以?BECD是菱形.
(3)解:当∠A=45°时,四边形BECD是正方形.
理由:因为∠ACB=90°,∠A=45°,所以∠ABC=∠A=45°.所以AC=BC.
又D为AB的中点,所以CD⊥AB,即∠CDB=90°.
又四边形BECD是菱形,所以菱形BECD是正方形.
图12
第 1 页 共 7 页
同课章节目录
