湘教版2018-2019学年度下学期八年级数学期末测试题含答案
文档属性
| 名称 | 湘教版2018-2019学年度下学期八年级数学期末测试题含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 259.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-11 00:00:00 | ||
图片预览



文档简介
期末测试题
一、选择题(每小题10分,共30分)
1. 下列图案中,既是轴对称图形又是中心对称图形的是( )
2.在平面直角坐标系中,若点M的坐标为(a,b),且在第二象限,则点N(-a,b)在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 下列各组数,可以作为直角三角形的三边长的是( )
A.1,2,3 B.32,42,52
C.,, D.,,
4. 已知□ABCD的周长为32,AB=4,则BC的长为( )
A. 4 B. 12 C. 24 D. 28
5. 一次函数y=3x-6的图象与x轴的交点坐标是( )
A. (0,-6) B. (0,6) C. (2,0) D. (-2,0)
6. 如图1,在菱形ABCD中,下列结论不一定成立的是( )
A. ∠1=∠2 B. AC⊥BD C. AB=AD D. AC=BD
图1
7. 在一个直角三角形中,若两直角边长分别为6 cm,8 cm,则下列结论不正确的是( )
A.斜边长为10 cm B.周长为25 cm
C.面积为24 cm2 D.斜边上的中线长为5 cm
8. 如图2,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8 B.6 C.4 D.2
图2
9. 在四边形ABCD中,对角线AC,BD相交于点O,下列各组条件中,不能判定四边形ABCD为矩形的是( )
A.∠A=∠B=90°,AC=BD B.AO=CO,BO=DO,∠A=90°
C.∠A=∠C,∠B+∠C=180°,AC⊥BD D.AB=CD,AD=BC,AC=BD
10. 如图3所示,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以对角线OA1为边作正方形OA1A2B1,再以对角线OA2为边作正方形OA2A3B2,……依此规律,则点A8的坐标是( )
A.(-8,0) B.(0,8)
C.(0,8) D.(0,16)
图3
二、填空题(每小题3分,共24分)
11.在英文单词“believe”中,字母“e”出现的频率是 .
12. 线段EF是由线段PQ平移得到的,点P(-1,4)的对应点为E(4,7),则点Q(-3,1)的对应点F的坐标为 .
13. 在□ABCD中,对角线AC,BD相交于点O,E是AB的中点,OE=4 cm,则AD的长是_________cm.
14. 已知一次函数y=kx+b的图象经过点A(x1,1),B(x2,-2),若x1<x2,则k____0(填“>”“<”或“=”).
15. 已知一个多边形的每个外角都相等,一个内角与一个外角的度数之比为9∶2,则这个多边形的边数为___.
16. 如图4所示,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB的长为半径画弧,交x轴正半轴于点C,则点C的坐标为_______.
图4
17. 若□ABCD的对角线AC,BD相交点O,△OAB是等边三角形,且AB=3,则□ABCD的面积是________.
18. 一个装有进水管和出水管的容器,从某时刻开始的4分内只进水不出水,在随后的8分内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分的进水量和出水量是两个常数,容器内的水量y(升)与时间x(分)之间的部分关系图象如图5所示,那么从关闭进水管起_______分该容器内的水恰好放完.
图5
三、解答题(共66分)
19. (8分)如图6所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC(顶点在网格线的交点的三角形)的顶点A,C的坐标分别为(-4,5),(-1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A1B1C1,并分别写出点A1,B1,C1的坐标.
图6
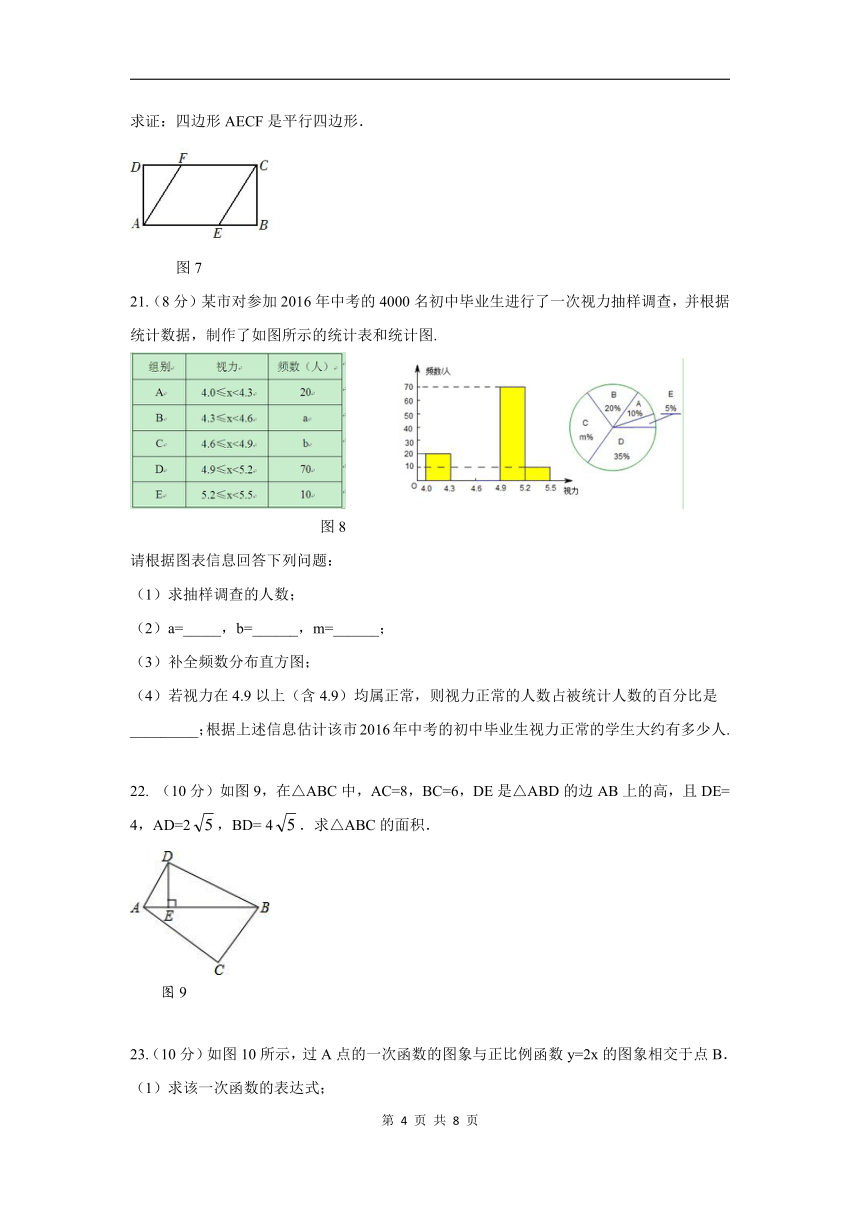
20.(8分)如图7,在矩形ABCD中,点E,F分别在AB,CD边上,连接CE,AF,DF=BE,求证:四边形AECF是平行四边形.
图7
21.(8分)某市对参加2016年中考的4000名初中毕业生进行了一次视力抽样调查,并根据统计数据,制作了如图所示的统计表和统计图.
图8
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)a=_____,b=______,m=______;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是_________;根据上述信息估计该市2016年中考的初中毕业生视力正常的学生大约有多少人.
22. (10分)如图9,在△ABC中,AC=8,BC=6,DE是△ABD的边AB上的高,且DE= 4,AD=2,BD= 4.求△ABC的面积.
图9
23.(10分)如图10所示,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B.
(1)求该一次函数的表达式;
(2)判断点C(4,-2)是否在该一次函数的图象上?说明理由;
(3)若该一次函数的图象与x轴交于点D,求△BOD的面积.
图10
24.(10分)如图11所示,在矩形纸片ABCD中,CD=12,BC=16,点E在AB上,将
△DAE沿DE折叠,使点A落在对角线BD上的点A1处,求AE的长度.
图11
25.(12分)如图12所示,已知四边形ABCD为正方形,AB=2,E为对角线AC上一动点,连接DE,过点E作EF⊥DE交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)试探究CE+CG的值是定值吗?若是,求出这个定值;若不是,请说明理由.
图12
期末测试题参考答案
一、1. C 2. A 3. C 4. B 5. C 6. D 7. B 8. C 9.C 10. D
二、11. 12. (2,4) 13. 8 14. < 15. 11 16.(2-2,0) 17. 9
18. 8
19. 解:(1)如图1所示;
(2)如图1所示,A1(4,5),B1(2,1),C1(1,3).
图1
20. 证明:因为四边形ABCD是矩形,所以DC=AB,DC∥AB.
因为DF=BE,所以DC-DF=AB-BE.
所以FC=AE.
因为DC∥AB,所以FC∥AE.
所以四边形AECF是平行四边形.
21.解:(1)抽样调查的人数为:20÷10%=200(人).
(2)40 60 30
(3)补全统计图略.
(4)40%;
该市2016年中考的初中毕业生视力正常的学生大约有:4000×40%=1600(人).
22. 解:因为DE是AB边上的高,所以∠AED=∠BED=90°.
在Rt△ADE中,由勾股定理,得AE2=AD2-DE2=(2)2-42=4,即AE=2.
同理,在Rt△BDE中,由勾股定理,得BE2=BD2-DE2=(4)2-42=64,即BE=8.
所以AB=10.
在△ABC中,因为AB2=AC2+BC2,所以△ABC是直角三角形.
所以△ABC的面积是AC·BC=×8×6=24.
23. 解:(1)由题意,将x=1代入y=2x,得y=2,则点B的坐标是(1,2).
设一次函数的表达式是y=kx+b.
将点A(0,3),B(1,2)代入,得解得
则一次函数的表达式是y=-x+3.
(2)因为x=4时,y=-1,所以点C(4,-2)不在该一次函数的图象上.
(3)一次函数的表达式为y=-x+3,令y=0,得x=3,则点D的坐标是(3,0).
所以S△BOD=OD×2=×3×2=3.
24. 证明:因为四边形ABCD是矩形,
所以∠A=∠C=90°,DA=BC,DC=AB.
在Rt△BCD中,CD=12,BC=16,由勾股定理,得BD=20.
由折叠的性质,得DA1=DA=16,∠DA1E=∠DAE=90°.
设AE=x,则A1E=x,BE=12-x,BA1=20-16=4.
在Rt△EA1B中,(12-x)2=x2+42,解得x=,即AE的长为.
25.证明:(1)过E作EM⊥BC于点M,过E作EN⊥CD于点N,如图2所示.
因为四边形ABCD是正方形,所以∠BCD=90°,∠ECN=45°.
所以∠EMC=∠ENC=∠BCD=90°,NE=NC.
所以四边形EMCN为正方形.所以EM=EN.
因为四边形DEFG是矩形,所以∠DEF=90°.
所以∠DEN+∠NEF=∠FEM+∠NEF=90°.
所以∠DEN=∠FEM.
又EM⊥BC,EN⊥CD,所以∠DNE=∠FME=90°.
在△DEN和△FEM中,∠DNE=∠FME,EN=EM,∠DEN=∠FEM,所以△DEN≌△FEM.
所以ED=EF.所以矩形DEFG为正方形.
图2
(2)CE+CG的值为定值.
理由:因为矩形DEFG为正方形,
所以DE=DG,∠EDC+∠CDG=90°.
因为四边形ABCD是正方形,
所以AD=DC,∠ADE+∠EDC=90°.所以∠ADE=∠CDG.
在△ADE和△CDG中,AD=CD,∠ADE=∠CDG,DE=DG,
所以△ADE≌△CDG.所以AE=CG.
所以AC=AE+CE=AB=×2=4.所以CE+CG=4,是定值.
第 1 页 共 8 页
同课章节目录
