华师大版八年级数学下册第17章 函数及其图象测试题(二)含答案
文档属性
| 名称 | 华师大版八年级数学下册第17章 函数及其图象测试题(二)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 407.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-11 15:44:39 | ||
图片预览


文档简介
第17章 函数及其图象测试题(二)
(本试卷满分100分)
一、选择题(本大题共10小题,每小题3分,共30分)
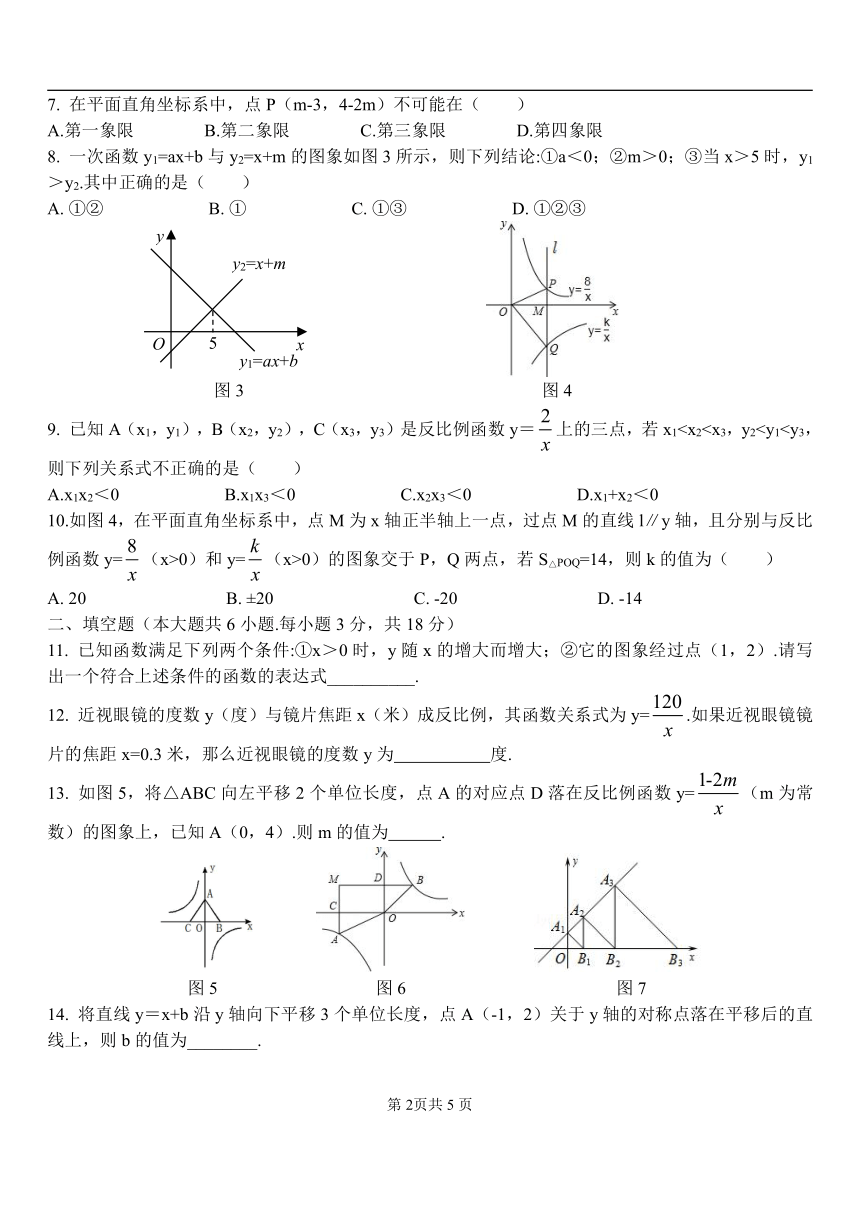
1. 下列图象中,表示y是x的函数的有( )
A.1个 B.2个 C.3个 D.4个
2. 下列函数中,y随x的增大而减少的是( )
A.y=2x+8 B.y=-2+4x C.y=-2x+8 D.y=-
3. 一次函数y=-x+4的图象是( )
4. 如图1,AB∥CD,AD∥BC∥x轴,则下列说法正确的是( )
A. A与D的横坐标相同 B. A与B的横坐标相同
C. B与C的纵坐标相同 D. C与D的纵坐标相同
图1 图2
5. 一次函数y=kx+b满足kb>0,且y随x的增大而减小,则此函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6. 如图2,已知一次函数y=ax+b和反比例函数y=的图象相交于A(-2,y1),B(1,y2)两点,则不等式ax+b<的解集为( )
A.x<-2或0<x<1 B.x<-2 C.0<x<1 D.-2<x<0或x>1
7. 在平面直角坐标系中,点P(m-3,4-2m)不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8. 一次函数y1=ax+b与y2=x+m的图象如图3所示,则下列结论:①a<0;②m>0;③当x>5时,y1>y2.其中正确的是( )
A. ①② B. ① C. ①③ D. ①②③
图3 图4
9. 已知A(x1,y1),B(x2,y2),C(x3,y3)是反比例函数y=上的三点,若x1
10.如图4,在平面直角坐标系中,点M为x轴正半轴上一点,过点M的直线l∥y轴,且分别与反比例函数y=(x>0)和y=(x>0)的图象交于P,Q两点,若S△POQ=14,则k的值为( )
A. 20 B. ±20 C. -20 D. -14
二、填空题(本大题共6小题.每小题3分,共18分)
11. 已知函数满足下列两个条件:①x>0时,y随x的增大而增大;②它的图象经过点(1,2).请写出一个符合上述条件的函数的表达式__________.
12. 近视眼镜的度数y(度)与镜片焦距x(米)成反比例,其函数关系式为y=.如果近视眼镜镜片的焦距x=0.3米,那么近视眼镜的度数y为 度.
13. 如图5,将△ABC向左平移2个单位长度,点A的对应点D落在反比例函数y=(m为常数)的图象上,已知A(0,4).则m的值为 .
图5 图6 图7
14. 将直线y=x+b沿y轴向下平移3个单位长度,点A(-1,2)关于y轴的对称点落在平移后的直线上,则b的值为________.
15. 如图6,在平面直角坐标系中,过点M(-3,2)分别作x轴,y轴的垂线与反比例函数y=的图象交于A,B两点,则四边形MAOB的面积为 .
16. 如图7,直线y=x+2交y轴于点A1,在x轴正方向上取点B1,使OB1=OA1;过点B1作A2B1⊥x轴,交l于点A2,在x轴正方向上取点B2,使B1B2=B1A2;过点B2作A3B2⊥x轴,交l于点A3,在x轴正方向上取点B3,使B2B3=B2A3……记△OA1B1面积为S1,△B1A2B2面积为S2,△B2A3B3面积为S3,…则S2018等于 .
三、解答题(本大题共7小题,共52分)
17. (5分)(2018年舟山)小红帮弟弟荡秋千,秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图8所示.
(1)根据函数的定义,请判断变量h是否为关于t的函数?
(2)结合图象回答:
①当t=0.7?s时,h的值是多少?并说明它的实际意义.
②秋千摆动第一个来回需多少时间?
18. (6分)已知y=(k-1)x|k|-k是一次函数.
(1)求k的值;
(2)若点(2,a)在这个一次函数的图象上,求a的值.
19. (6分)已知y-2与x+1成正比例函数关系,且x=-2时,y=6.
(1)写出y与x之间的函数表达式;
(2)求当x=-3时,y的值;
(3)求当y=4时,x的值.
20. (8分)在直角坐标系中,一条直线经过A(-1,5),P(-2,a),B(3,-3)三点.
(1)求a的值;
(2)设这条直线与y轴相交于点D,求△OPD的面积.
21. (8分)五一期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游(如图9).
根据以上信息,解答下列问题:
(1)租用时间为x(小时),租用甲公司的车所需费用为y1(元),租用乙公司的车所需费用为y2(元),分别求出y1,y2与x的函数关系式;
(2)当租车时间为多少小时时,两种方案所需费用相同;
(3)根据(2)的计算结果,结合图象,帮小明确定选择哪种出游方案更合算.
22. (9分)如图10,直线y1=-x+4,y2=x+b都与双曲线y=交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出y2>y的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1∶3两部分,求此时点P的坐标.
23. (10分)如图11,制作某种食品的同时需将原材料加热,设该材料的温度为y ℃,从加热开始计算时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4 ℃,加热一段时间使材料温度达到28 ℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14 ℃.
(1)分别求出该材料加热和停止加热过程中y与x的函数表达式(写出x的取值范围);
(2)根据该食品的制作要求,在材料温度不低于12 ℃的这段时间内,需要对该材料进行特殊处理,那么对该材料进行特殊处理的时间为多少分钟?
附加题(20分,不计入总分)
24. 小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行跟踪记录,并将记录情况绘成图象,日销售量y(千克)与上市时间x(天)的函数关系如图12-①所示,樱桃价格z(元/千克)与上市时间x(天)的函数关系式如图12-②所示.
(1)观察图象,直接写出日销售量的最大值;
(2)求小明家樱桃的日销售量y与上市时间x的函数表达式;
(3)试比较第10天与第12天的销售金额哪天多?
参考答案
一、1. B 2. C 3. D 4. C 5. A 6. D 7. A 8. B 9. A 10. C
二、11. 答案不唯一,如y=2x 12. 400 13. 14. 4 15. 10 16.
三、17. 解:(1)变量h是关于t的函数;
(2)①当t=0.7 s时,h=0.5 m,它的实际意义是秋千摆动0.7 s时,离地面的高度是0.5 m.
②秋千摆动第一个来回需2.8 s.
18. (1)k=-1.(2)a=-3.
19. 解:(1)设y-2=k(x+1)(k≠0),因为x=-2时,y=6,所以6-2=k(-2+1),解得k=-4,所以y=-4x-2.
(2)当x=-3时,代入y=-4x-2,得y=(-4)×(-3)-2=10.
(3)当y=4时,代入y=-4x-2,得4=-4x-2,解得x=-.
20. 解:(1)设直线的表达式为y=kx+b(k≠0),把A(-1,5),B(3,-3)代入,得,解得,所以直线的表达式为y=-2x+3,把P(-2,a)代入y=-2x+3,得a=7.
(2)由(1)可知点P的坐标为(-2,7),当x=0时,y=3,所以直线与y轴的交点坐标为(0,3),所以S△OPD=×3×2=3.
21. 解:(1)因为的图象过点D(m,2),E(n,),所以.因为AB=BD=2,所以n=m+2.所以解得所以D(1,2).所以k=2.所以反比例函数的表达式为.
(2)连接OD,OE.因为S△ODC=S△AOE==1,所以S四边形OEBD=S四边形OABC-S△ODC-S△AOE=6﹣2=4.
22. 解:(1)把A(1,m)代入y1=-x+4,可得m=-1+4=3,所以A(1,3).
把A(1,3)代入双曲线y=,可得k=1×3=3,所以y与x之间的函数关系式为y=.
(2)因为A(1,3),所以y2>y的解集为x>1.
(3)y1=-x+4,令y=0,则x=4,所以点B的坐标为(4,0).
把A(1,3)代入y2=x+b,可得3=+b,所以b=,所以y2=x+.
令y=0,则x=-3,即C(-3,0),所以BC=7.
因为AP把△ABC的面积分成1∶3两部分,所以CP=BC=或BP=BC=.所以OP=3-=或OP=4-=.所以P(-,0)或(,0).
23. (1)设停止加热后反比例函数的表达式为y=,因为y=过点(12,14),所以k1=12×14=168,所以y=.当y=28时,28=,解得x=6.
设加热过程中一次函数的表达式为y=k2x+b,因为y=k2x+b的图象过点(0,4),(6,28),所以解得
所以加热过程中的函数表达式为y=4x+4,此时x的取值范围是0≤x≤6;停止加热后的函数表达式为y=,此时x的取值范围是x>6.
(2)当y=12时,代入y=4x+4,得x=2;代入y=,得x=14.所以对该材料进行特殊处理的时间为14-2=12(分钟).
24. 解:(1)120千克.
(2)当0≤x≤12时,设日销售量与上市的时间的函数表达式为y=kx(k≠0),
因为点(12,120)在y=kx的图象上,所以k=10,所以函数表达式为y=10x,
当12<x≤20时,设日销售量与上市时间的函数表达式为y=kx+b(k≠0),
因为点(12,120),(20,0)在y=kx+b的图象上,所以所以
所以函数表达式为y=-15x+300.
所以小明家樱桃的日销量y与上市时间x的函数表达式为y=.
(3)当5<x≤15时,设樱桃价格与上市时间的函数表达式为z=kx+b,
因为点(5,32),(15,12)在z=kx+b的图象上,所以,所以所以函数表达式为z=-2x+42.
当x=10时,y=10×10=100,z=-2×10+42=22,销售金额为100×22=2200(元).
当x=12时,y=120,z=-2×12+42=18,销售金额为120×18=2160(元).
因为2200>2160,所以第10天的销售金额多.
x
y
4
A
O
-4
x
y
4
B
O
-4
4
x
y
4
D
O
x
y
C
O
-4
-4
x
y
O
5
y2=x+m
y1=ax+b
②
①
图12
第9页共5页
