人教版八年级下册数学:20.2 数据的波动程度(方差)(25张PPT)
文档属性
| 名称 | 人教版八年级下册数学:20.2 数据的波动程度(方差)(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-11 20:14:49 | ||
图片预览








文档简介
20.2 数据的波动程度
有甲、乙两台包装机同时包装糖果,现从中各抽取10袋,称得它们的实际重量如下:
甲:500,503,498,505,490,501,511,497,508,499
乙:501,499,502,505,498,501,500,503,491,512
糖果厂准备从这两种型号包装机中挑选一种进行糖果包装.
该如何选择呢?
学习目标
1.知道方差的意义及其作用.
2.会求一组数据的方差.
3.会用方差的知识解决实际问题.
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
根据上表求出两组数据的平均数分别是:
说明在试验田中,甲、乙两种甜玉米的平均产量相差不大.
可估计这个地区种植这两种甜玉米的平均产量相差不大.
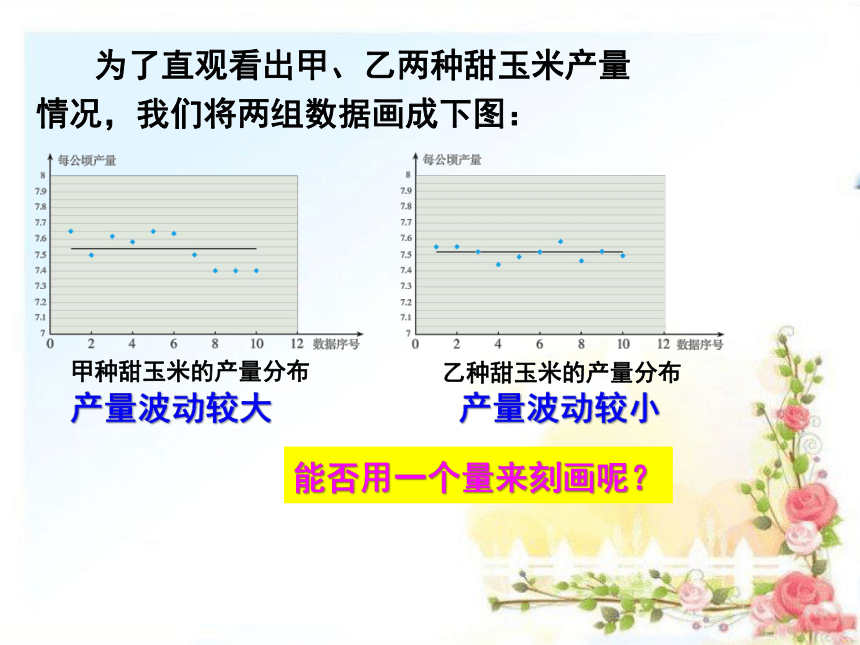
为了直观看出甲、乙两种甜玉米产量情况,我们将两组数据画成下图:
甲种甜玉米的产量分布
乙种甜玉米的产量分布
产量波动较大
产量波动较小
能否用一个量来刻画呢?
统计学中常采用下面的做法:
设有n个数据x1,x2,…,xn,各数据与它们的平均数 差的平方分别是
我们用这些值的平均数,即
来衡量这组数据波动的大小,并把它叫做这组数据的方差,记作s2.
方差可以反映数据的波动程度;方差越大,说明数据的波动越大;方差越小,说明数据的波动越小.
分析甲、乙两种甜玉米的波动程度:
s2甲>s2乙
∴乙种甜玉米的产量比较稳定
例1 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)如下图所示:
哪个芭蕾舞团女演员的身高更整齐?
解:甲、乙两团演员的身高平均数分别是
方差分别是
1. 如果一组数据a1,a2,…,an的平均数为 ,方差为s2,那么,另一组数据a1+2,a2+2,…,an+2的平均数为 ,方差为 .
s2
2. 如果一组数据b1,b2,…,bn的平均数为4,方差为 ,那么另一组数据 的平均数为 ,方差为 .
2
1. 将一组数据中的每一个数据都加上(或减去)同一个常数,所得的一组新数据的方差不变.
2. 将一组数据中的每一个数据都变为原来的k倍,所得的一组新数据的方差变为原数据方差的k2倍.
1.用条形图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的:
(1)6 6 6 6 6 6 6
(2)5 5 6 6 6 7 7
(3)3 3 4 6 8 9 9
(4)3 3 3 6 9 9 9
解:
2.如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图,观察图形,甲、乙这10次射击成绩的方差s2甲,s2乙哪个大?
解:甲、乙这10次射击成绩的平均数分别是
方差分别是
基础巩固
1.已知一个样本的方差
,
则这个样本的容量为 ,平均数为 .
10
26
2.甲、乙两名运动员进行了5次跳远的成绩测试,且知s2甲=0.016,s2乙=0.025,由此可知 的成绩比 的成绩稳定.
甲
乙
综合应用
3.若已知一组数据x1,x2,…,xn的平均数为 ,方差为s2,那么,另一组数据3x1-2,3x2-2,…,3xn-2 的平均数为 ,方差为 .
9s2
4.一组数据的方差为s2,将这组数据中的每一个数据都除以2,所得新数据的方差是( )
A. B.2s2 C. D.4s2
C
误 区 诊 断
试比较下列两组数据的稳定性.
A组:10,5,5,5,5,5,5,0,5,5;
B组: 2,8,5,4,5,7,3,6,1,9.
∵A组的平均数是5,方差为5;B组的平均数是5,方差为6,∴ A组数据的波动较大.
∵A组的平均数为5,方差为5;B组的平均数为5,方差为6.两组数据平均数一样,但是A组的方差比 B组的方差小,∴B组数据的波动较大.
错解:
正解:
错因分析:导致出错的原因是误认为方差越小,波动越大,对方差的意义理解错误.
方差是用来衡量一组数据的波动大小的特征量
方差越大,数据的波动越大;方差越小,数据的波动越小,通过比较方差的大小来判断数据的稳定性.
甲、乙两台机床生产同种零件,10天出的次品个数分别是:
甲:0,1,0,2,2,0,3,1,2,4
乙:2,3,1,2,0,2,1,1,2,1
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
解:
s2甲>s2乙
∴乙台机床的性能较好
有甲、乙两台包装机同时包装糖果,现从中各抽取10袋,称得它们的实际重量如下:
甲:500,503,498,505,490,501,511,497,508,499
乙:501,499,502,505,498,501,500,503,491,512
糖果厂准备从这两种型号包装机中挑选一种进行糖果包装.
该如何选择呢?
学习目标
1.知道方差的意义及其作用.
2.会求一组数据的方差.
3.会用方差的知识解决实际问题.
根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
根据上表求出两组数据的平均数分别是:
说明在试验田中,甲、乙两种甜玉米的平均产量相差不大.
可估计这个地区种植这两种甜玉米的平均产量相差不大.
为了直观看出甲、乙两种甜玉米产量情况,我们将两组数据画成下图:
甲种甜玉米的产量分布
乙种甜玉米的产量分布
产量波动较大
产量波动较小
能否用一个量来刻画呢?
统计学中常采用下面的做法:
设有n个数据x1,x2,…,xn,各数据与它们的平均数 差的平方分别是
我们用这些值的平均数,即
来衡量这组数据波动的大小,并把它叫做这组数据的方差,记作s2.
方差可以反映数据的波动程度;方差越大,说明数据的波动越大;方差越小,说明数据的波动越小.
分析甲、乙两种甜玉米的波动程度:
s2甲>s2乙
∴乙种甜玉米的产量比较稳定
例1 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)如下图所示:
哪个芭蕾舞团女演员的身高更整齐?
解:甲、乙两团演员的身高平均数分别是
方差分别是
1. 如果一组数据a1,a2,…,an的平均数为 ,方差为s2,那么,另一组数据a1+2,a2+2,…,an+2的平均数为 ,方差为 .
s2
2. 如果一组数据b1,b2,…,bn的平均数为4,方差为 ,那么另一组数据 的平均数为 ,方差为 .
2
1. 将一组数据中的每一个数据都加上(或减去)同一个常数,所得的一组新数据的方差不变.
2. 将一组数据中的每一个数据都变为原来的k倍,所得的一组新数据的方差变为原数据方差的k2倍.
1.用条形图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度的:
(1)6 6 6 6 6 6 6
(2)5 5 6 6 6 7 7
(3)3 3 4 6 8 9 9
(4)3 3 3 6 9 9 9
解:
2.如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图,观察图形,甲、乙这10次射击成绩的方差s2甲,s2乙哪个大?
解:甲、乙这10次射击成绩的平均数分别是
方差分别是
基础巩固
1.已知一个样本的方差
,
则这个样本的容量为 ,平均数为 .
10
26
2.甲、乙两名运动员进行了5次跳远的成绩测试,且知s2甲=0.016,s2乙=0.025,由此可知 的成绩比 的成绩稳定.
甲
乙
综合应用
3.若已知一组数据x1,x2,…,xn的平均数为 ,方差为s2,那么,另一组数据3x1-2,3x2-2,…,3xn-2 的平均数为 ,方差为 .
9s2
4.一组数据的方差为s2,将这组数据中的每一个数据都除以2,所得新数据的方差是( )
A. B.2s2 C. D.4s2
C
误 区 诊 断
试比较下列两组数据的稳定性.
A组:10,5,5,5,5,5,5,0,5,5;
B组: 2,8,5,4,5,7,3,6,1,9.
∵A组的平均数是5,方差为5;B组的平均数是5,方差为6,∴ A组数据的波动较大.
∵A组的平均数为5,方差为5;B组的平均数为5,方差为6.两组数据平均数一样,但是A组的方差比 B组的方差小,∴B组数据的波动较大.
错解:
正解:
错因分析:导致出错的原因是误认为方差越小,波动越大,对方差的意义理解错误.
方差是用来衡量一组数据的波动大小的特征量
方差越大,数据的波动越大;方差越小,数据的波动越小,通过比较方差的大小来判断数据的稳定性.
甲、乙两台机床生产同种零件,10天出的次品个数分别是:
甲:0,1,0,2,2,0,3,1,2,4
乙:2,3,1,2,0,2,1,1,2,1
分别计算出两个样本的平均数和方差,根据你的计算判断哪台机床的性能较好?
解:
s2甲>s2乙
∴乙台机床的性能较好
