八下数学18.2.2菱形性质与判定课件(30张ppt)
文档属性
| 名称 | 八下数学18.2.2菱形性质与判定课件(30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-12 08:31:00 | ||
图片预览




文档简介
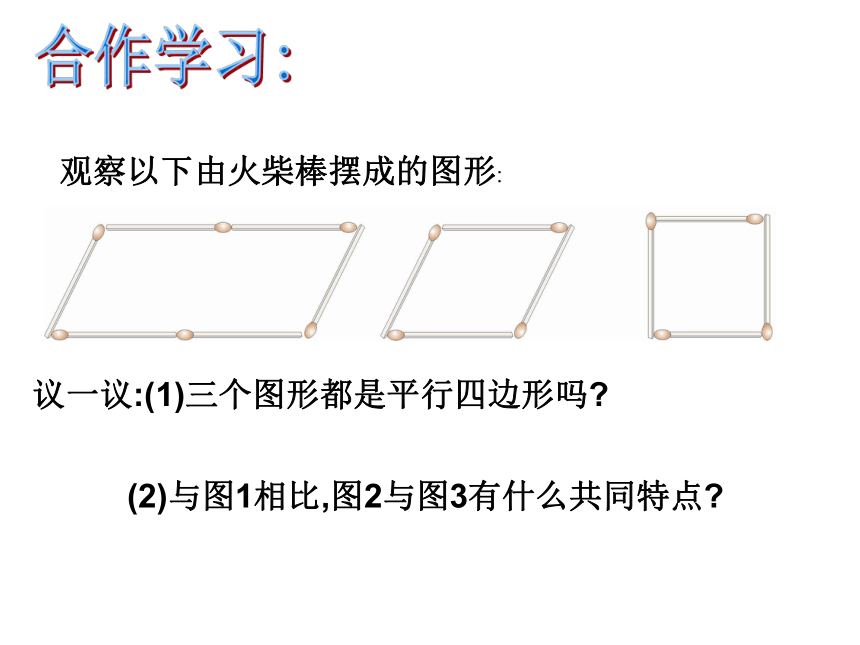
观察以下由火柴棒摆成的图形:
议一议:(1)三个图形都是平行四边形吗?
(2)与图1相比,图2与图3有什么共同特点?
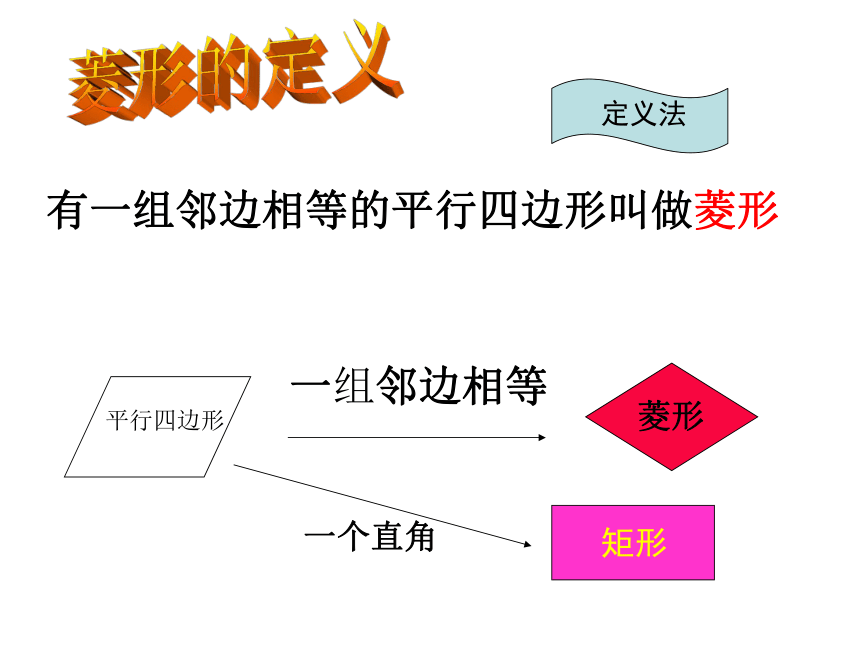
有一组邻边相等的平行四边形叫做菱形
一组邻边相等
定义法
矩形
一个直角
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
图片欣赏
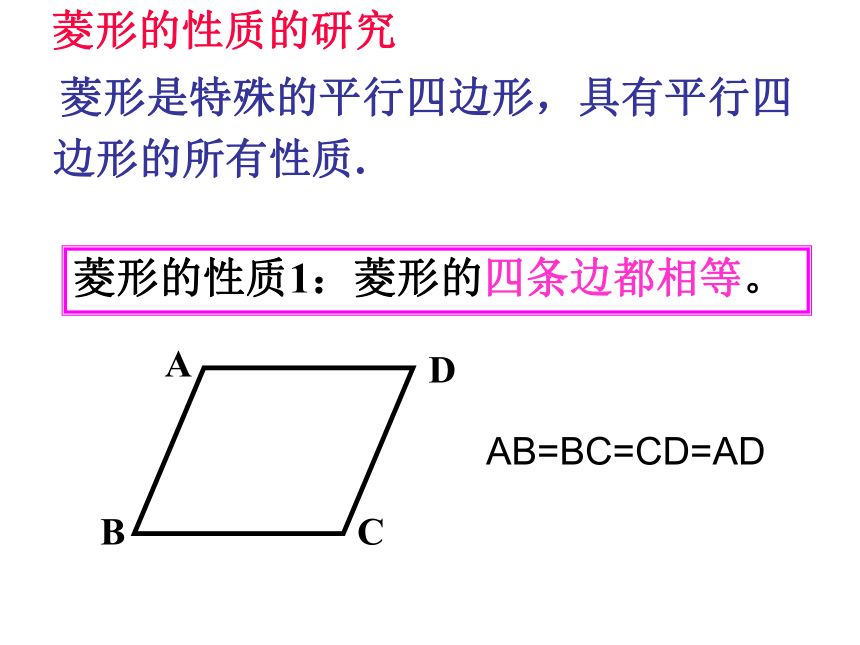
菱形的性质1:菱形的四条边都相等。
菱形是特殊的平行四边形,具有平行四边形的所有性质.
菱形的性质的研究
AB=BC=CD=AD
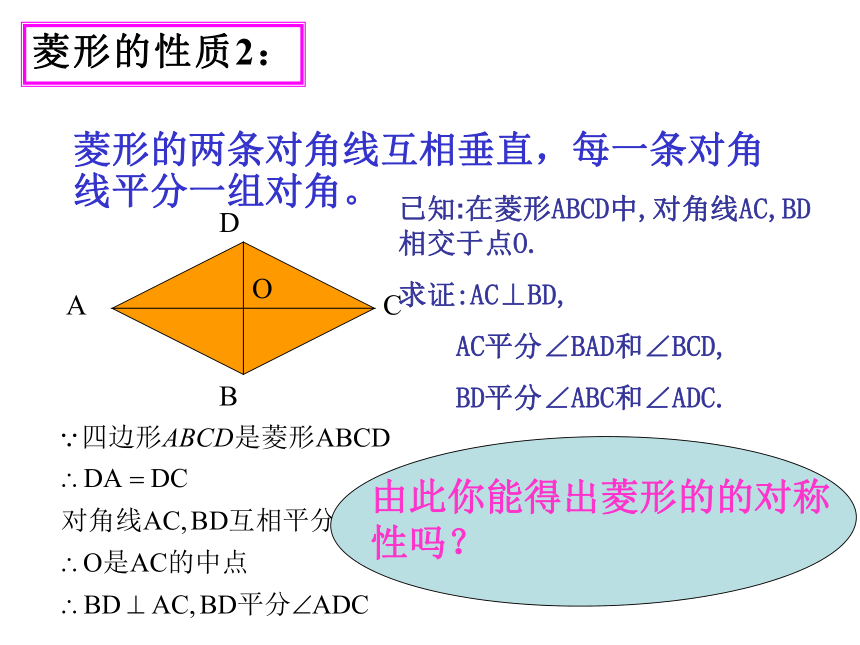
菱形的性质2:
菱形的两条对角线互相垂直,每一条对角 线平分一组对角。
已知:在菱形ABCD中,对角线AC,BD相交于点O.
求证:AC⊥BD,
AC平分∠BAD和∠BCD,
BD平分∠ABC和∠ADC.
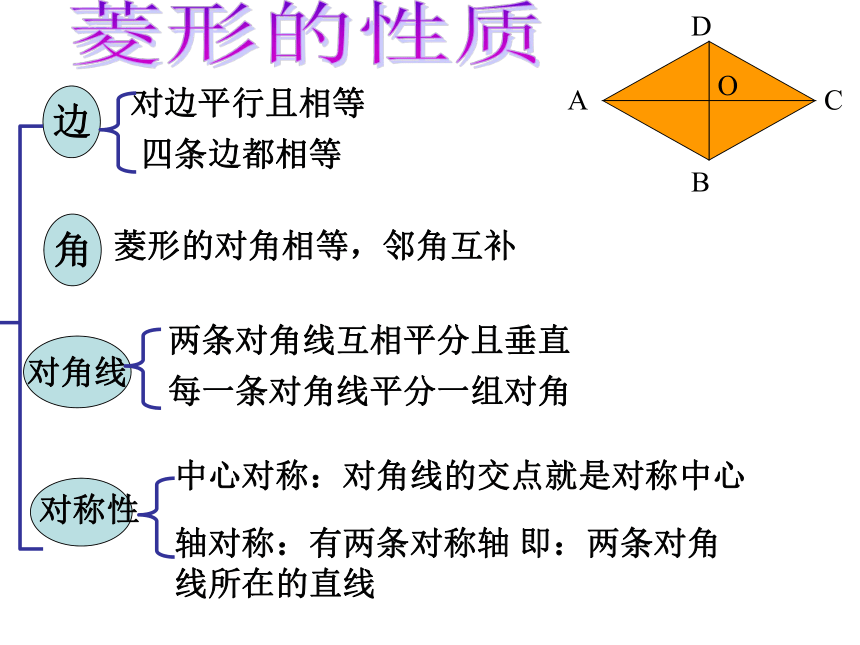
两条对角线互相平分且垂直
对边平行且相等
边
对角线
角
四条边都相等
菱形的对角相等,邻角互补
每一条对角线平分一组对角
中心对称:对角线的交点就是对称中心
轴对称:有两条对称轴 即:两条对角 线所在的直线
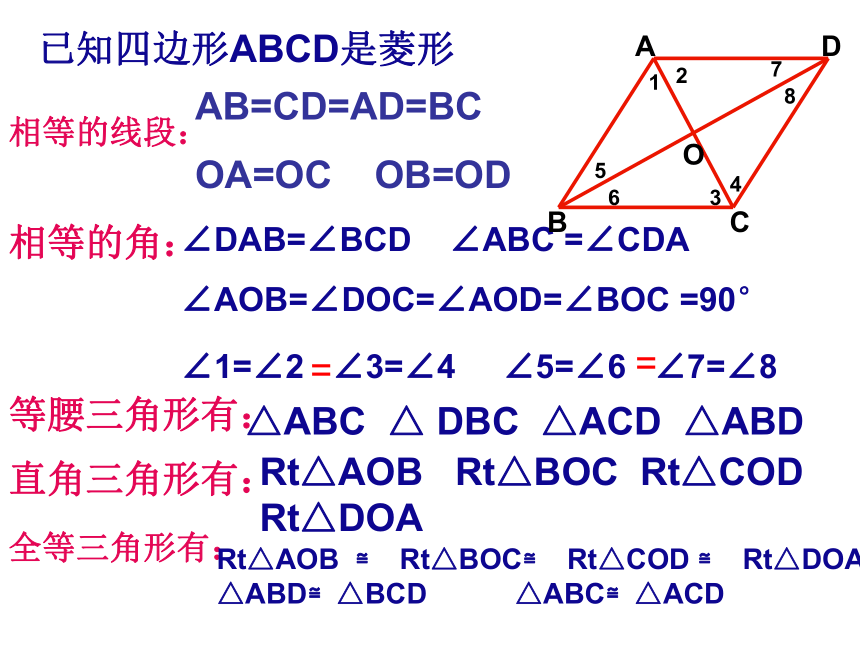
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
已知四边形ABCD是菱形
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2 ∠3=∠4 ∠5=∠6 ∠7=∠8
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
=
=
.
.
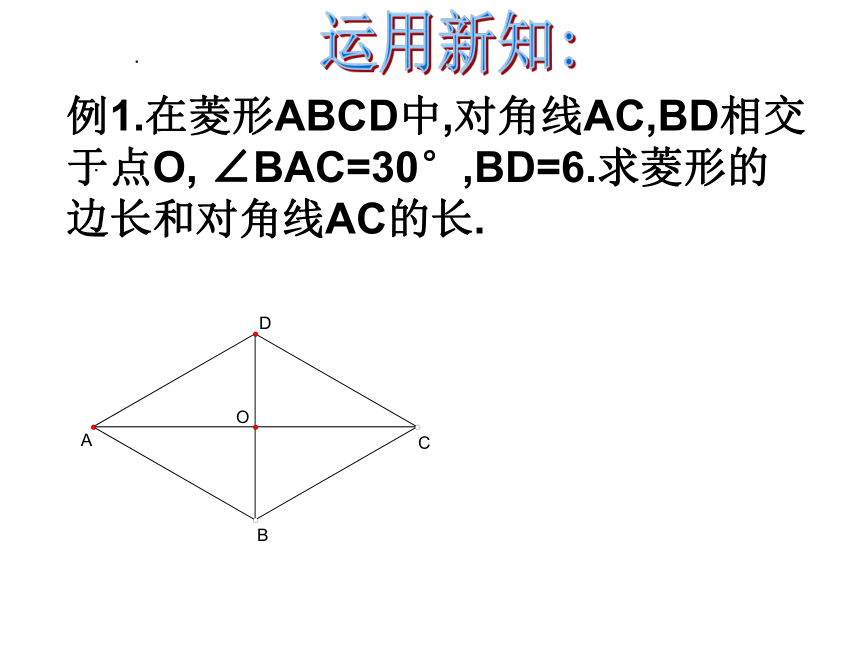
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
1.菱形具有而矩形不一定有的性质是 ( )
(A) 对角线互相平分 (B) 四条边都相等
(C) 对角相等 (D) 邻角互补
B
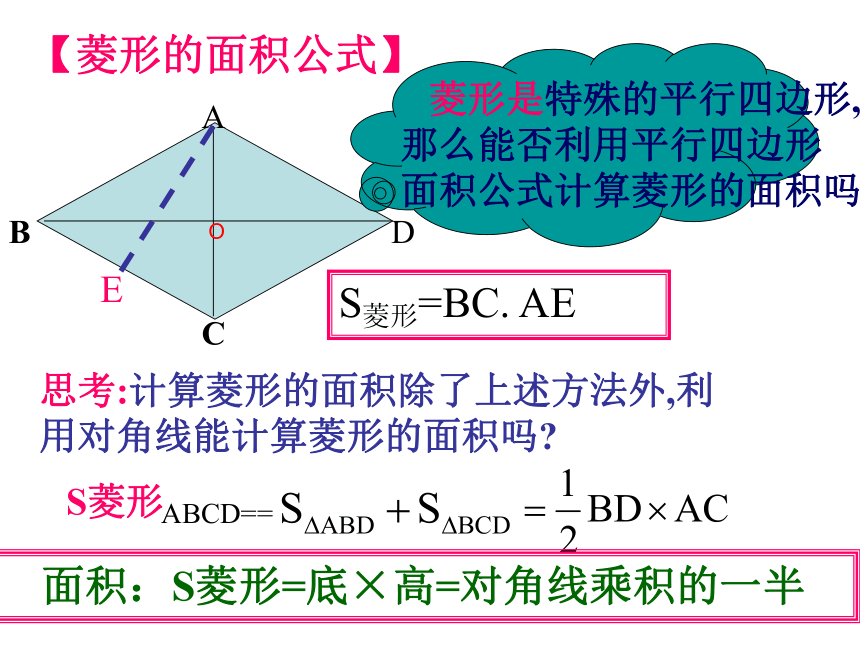
【菱形的面积公式】
A
B
C
D
E
S菱形=BC. AE
思考:计算菱形的面积除了上述方法外,利用对角线能计算菱形的面积吗?
面积:S菱形=底×高=对角线乘积的一半
O
判定方法1:有一组邻边相等的平行四边形是菱形
∵ 四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形
菱形判定方法的研究
判定定理2对角线互相垂直的平行四边形是菱形
已知 ABCD中,对角线AC、BD互相垂直,
求证:四边形ABCD是菱形.
证明:在 中,OA=OC
( ① ).
又∵AC⊥BD,
∴ BD所在直线是线段AC的垂直平分线,
∴ AB=BC,
∴ 四边形ABCD是菱形
( ② ).
例 已知:矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形
证明 ∵ 四边形ABCD是矩形,
∴ AE∥FC( ① )
∴ ∠1=∠2.( ② )
∵ EF平分AC,
∴ AO=OC.
又∵ ∠AOE=∠COF=90°,
∴ △AOE≌△COF( ③ ),
∴ EO=FO,
∴ 四边形AFCE是平行四边形( ④ )
又∵EF⊥AC,
∴ 四边形AFCE是菱形( ⑤ )
判定定理3:四条边都相等的四边形是菱形
已知:AB=BC=CD=DA
求证:四边形ABCD是菱形
∵AB=CD,BC=AD
∴四边形ABCD是平行四边形
∵AB=CD
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形是菱形)
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
菱形的判定:
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
一组邻边相等的平行四边形是菱形
文字语言 图形语言 符号语言
判定法一
判定
法二 对角线互相垂直的平行四边形是菱形
判定法三 四边相等的四边形是菱形
1.已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中∠ABC=60度,则∠BAC=_______.
3cm
60度
3、菱形的两条对角线长分别为6cm和8cm,则菱形的面积是( )
C
A.10 B.7 C. 24 D.48
3
4
4.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )
A.75°B.60°C.45°D.30°
B
6 已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD;
7、如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,
求证:EB=OA;
当堂检测:
1、判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形; ( )
╳
√
╳
2、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
矩
菱
矩
菱
(1).下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
(2).对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对
C
(3).下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BD
C
3、选择:
=
=
7、已知:如图,AD平分∠BAC,DE∥AC 交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴ □AEDF是菱形
证明:∵DE∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE∥AC
∴∠2=∠3
∵ AD是△ABC的角平分线
∴ ∠1=∠2
∴AE=DE
∴ ∠1=∠3
∟
∟
E
F
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
课后拓展1:
请你动脑筋
如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由。
课后拓展2:
┐
) 1
2 (
提示: △AOD≌△COB(角边角)
AD=BC
议一议:(1)三个图形都是平行四边形吗?
(2)与图1相比,图2与图3有什么共同特点?
有一组邻边相等的平行四边形叫做菱形
一组邻边相等
定义法
矩形
一个直角
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
图片欣赏
菱形的性质1:菱形的四条边都相等。
菱形是特殊的平行四边形,具有平行四边形的所有性质.
菱形的性质的研究
AB=BC=CD=AD
菱形的性质2:
菱形的两条对角线互相垂直,每一条对角 线平分一组对角。
已知:在菱形ABCD中,对角线AC,BD相交于点O.
求证:AC⊥BD,
AC平分∠BAD和∠BCD,
BD平分∠ABC和∠ADC.
两条对角线互相平分且垂直
对边平行且相等
边
对角线
角
四条边都相等
菱形的对角相等,邻角互补
每一条对角线平分一组对角
中心对称:对角线的交点就是对称中心
轴对称:有两条对称轴 即:两条对角 线所在的直线
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
已知四边形ABCD是菱形
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2 ∠3=∠4 ∠5=∠6 ∠7=∠8
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
=
=
.
.
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的边长和对角线AC的长.
1.菱形具有而矩形不一定有的性质是 ( )
(A) 对角线互相平分 (B) 四条边都相等
(C) 对角相等 (D) 邻角互补
B
【菱形的面积公式】
A
B
C
D
E
S菱形=BC. AE
思考:计算菱形的面积除了上述方法外,利用对角线能计算菱形的面积吗?
面积:S菱形=底×高=对角线乘积的一半
O
判定方法1:有一组邻边相等的平行四边形是菱形
∵ 四边形ABCD是平行四边形
AB=BC
∴四边形ABCD是菱形
菱形判定方法的研究
判定定理2对角线互相垂直的平行四边形是菱形
已知 ABCD中,对角线AC、BD互相垂直,
求证:四边形ABCD是菱形.
证明:在 中,OA=OC
( ① ).
又∵AC⊥BD,
∴ BD所在直线是线段AC的垂直平分线,
∴ AB=BC,
∴ 四边形ABCD是菱形
( ② ).
例 已知:矩形ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形
证明 ∵ 四边形ABCD是矩形,
∴ AE∥FC( ① )
∴ ∠1=∠2.( ② )
∵ EF平分AC,
∴ AO=OC.
又∵ ∠AOE=∠COF=90°,
∴ △AOE≌△COF( ③ ),
∴ EO=FO,
∴ 四边形AFCE是平行四边形( ④ )
又∵EF⊥AC,
∴ 四边形AFCE是菱形( ⑤ )
判定定理3:四条边都相等的四边形是菱形
已知:AB=BC=CD=DA
求证:四边形ABCD是菱形
∵AB=CD,BC=AD
∴四边形ABCD是平行四边形
∵AB=CD
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形是菱形)
菱形常用的判定方法:
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
菱形的判定:
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵在□ABCD中
AC⊥BD
∴四边形ABCD是菱形
∵在□ABCD中
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
一组邻边相等的平行四边形是菱形
文字语言 图形语言 符号语言
判定法一
判定
法二 对角线互相垂直的平行四边形是菱形
判定法三 四边相等的四边形是菱形
1.已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中∠ABC=60度,则∠BAC=_______.
3cm
60度
3、菱形的两条对角线长分别为6cm和8cm,则菱形的面积是( )
C
A.10 B.7 C. 24 D.48
3
4
4.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )
A.75°B.60°C.45°D.30°
B
6 已知:如图,AD平分∠BAC,DE∥AC交AB于E,DF∥AB交AC于F.
求证:EF⊥AD;
7、如图,E为菱形ABCD边BC上一点,且AB=AE,AE交BD于O,且∠DAE=2∠BAE,
求证:EB=OA;
当堂检测:
1、判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形; ( )
╳
√
╳
2、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
矩
菱
矩
菱
(1).下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形
C
(2).对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对
C
(3).下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BD
C
3、选择:
=
=
7、已知:如图,AD平分∠BAC,DE∥AC 交AB于E,DF∥AB交AC于F.
求证:四边形AEDF是菱形.
∴ □AEDF是菱形
证明:∵DE∥AC DF∥AB
∴四边形AEDF是平行四边形
∵ DE∥AC
∴∠2=∠3
∵ AD是△ABC的角平分线
∴ ∠1=∠2
∴AE=DE
∴ ∠1=∠3
∟
∟
E
F
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
课后拓展1:
请你动脑筋
如图,AD∥BC,BD垂直平分AC,四边形ABCD一定是菱形吗?若是,请说明理由。
课后拓展2:
┐
) 1
2 (
提示: △AOD≌△COB(角边角)
AD=BC
