第八章 平行线的有关证明综合测评(含答案)
文档属性
| 名称 | 第八章 平行线的有关证明综合测评(含答案) | 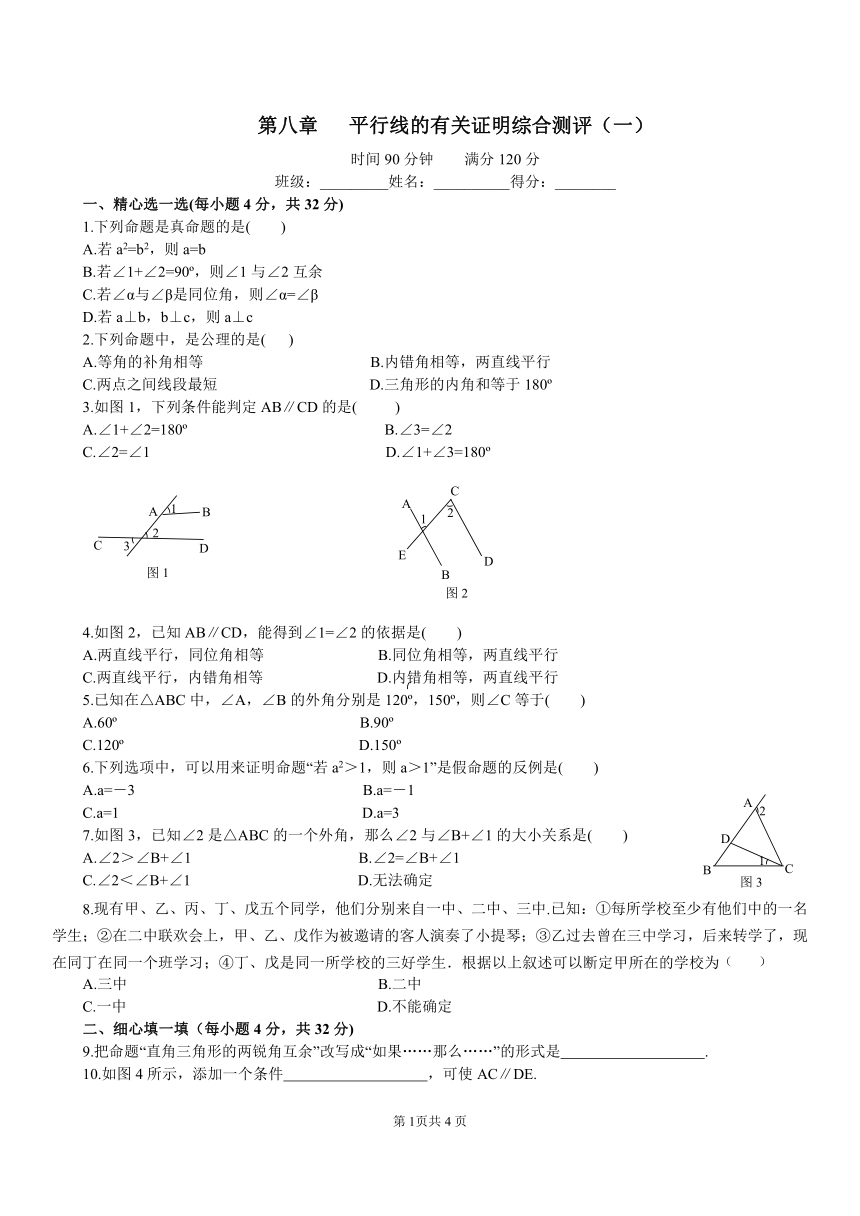 | |
| 格式 | zip | ||
| 文件大小 | 108.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-12 12:01:55 | ||
图片预览


文档简介
第八章 平行线的有关证明综合测评(一)
时间90分钟 满分120分
班级:_________姓名:__________得分:________
一、精心选一选(每小题4分,共32分)
1.下列命题是真命题的是( )
A.若a2=b2,则a=b
B.若∠1+∠2=90?,则∠1与∠2互余
C.若∠α与∠β是同位角,则∠α=∠β
D.若a⊥b,b⊥c,则a⊥c
2.下列命题中,是公理的是( )
A.等角的补角相等 B.内错角相等,两直线平行
C.两点之间线段最短 D.三角形的内角和等于180?
3.如图1,下列条件能判定AB∥CD的是( )
A.∠1+∠2=180? B.∠3=∠2
C.∠2=∠1 D.∠1+∠3=180?
4.如图2,已知AB∥CD,能得到∠1=∠2的依据是( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
5.已知在△ABC中,∠A,∠B的外角分别是120?,150?,则∠C等于( )
A.60? B.90?
C.120? D.150?
6.下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A.a=-3 B.a=-1
C.a=1 D.a=3
7.如图3,已知∠2是△ABC的一个外角,那么∠2与∠B+∠1的大小关系是( )
A.∠2>∠B+∠1 B.∠2=∠B+∠1
C.∠2<∠B+∠1 D.无法确定
8.现有甲、乙、丙、丁、戊五个同学,他们分别来自一中、二中、三中.已知:①每所学校至少有他们中的一名学生;②在二中联欢会上,甲、乙、戊作为被邀请的客人演奏了小提琴;③乙过去曾在三中学习,后来转学了,现在同丁在同一个班学习;④丁、戊是同一所学校的三好学生.根据以上叙述可以断定甲所在的学校为( )
A.三中 B.二中
C.一中 D.不能确定
二、细心填一填(每小题4分,共32分)
9.把命题“直角三角形的两锐角互余”改写成“如果……那么……”的形式是 .
10.如图4所示,添加一个条件 ,可使AC∥DE.
11.如图5,已知直线a∥b,小杜把直角三角尺的直角顶点放在直线b上,若∠1=18°,则∠3的度数为____________.
12.如图6,点D为BC延长线上的一点,∠A=∠ACB,∠A=2∠B,则∠ACD的度数为 .
13.下列几个命题:①若两个实数相等,则它们的平方相等;②若三角形的三边长a,b,c满足(a-b)(a+b)+c2=0;则这个三角形是直角三角形;③有两边和一角分别相等的两个三角形全等.其中是假命题的有_________(填序号).
14.如图7,把一个长方形ABCD纸片沿EF折叠后,点D,C分别落在D',C'的位置,若∠AED'=30?, 则∠CFE=_____________°.
如图8,把一块含有30°角(∠A=30°)的直角三角尺ABC的直角顶点放在长方形桌面CDEF(CD∥EF)的一个顶点C处,桌面的另一个顶点F与三角尺斜边相交于点F,如果∠1=40°,那么∠AFE=________°.
图8
16.小明同学连续观察了太原市2014年8月份某几天的天气情况,他的观察结果是:①共有5个下午是晴天;②共有7个上午是晴天;③共有8个半天是雨天;④下午下雨的那天上午是晴天,则该学生观察的天数为_________.
三、耐心做一做(共56分)
17.(10分)读句画图:如图9,直线CD与直线AB相交于点C,
根据下列语句画图:
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.
18.(10分)如图10,已知点B,D,G在同一条直线上,AB∥CD,∠1=∠2,请问BE与DF平行吗?为什么?
19.(10分)已知:如图11,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.
20.(12分)阅读理解:如果三角形满足一个角α是另一个角β的3倍时,那么我们称这个三角形为“智慧三角形”.其中α称为“智慧角”.
解答问题:
一个角为60?的直角三角形 (填“是”或“不是”)“智慧三角形”,若是,“智慧角”是 .
⑵已知一个“智慧三角形”的“智慧角”为108°,求这个“智慧三角形”各个角的度数.
21.(14分)数学活动课上,老师提出了一个问题:
我们知道,三角形的一个外角等于和它不相邻的两个内角的和,那么三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系?
(1)独立思考,请你完成老师提出的问题:
如图12所示,已知∠DBC和∠BCE分别为△ABC的两个外角,试探究∠A和∠DBC,∠BCE之间的数量关系.
解:
⑵合作交流,“创新小组”受此问题的启发:分别作外角∠CBD和∠BCE的平分线BF和CF,交于点F(如图13所示),那么∠A与∠F之间有何数量关系?请写出解答过程.
第八章 平行线的有关证明综合测评(一)参考答案
一、1.B 2.C 3.C 4.C 5.B 6.A 7.A 8.A
二、9.如果一个三角形是直角三角形,那么这个三角形的两锐角互余 10.答案不唯一,如∠A=∠BDE
11.72? 12.108? 13. ③ 14.105 15.10
16.10天 提示:由题意知,小明同学每天测两次,共测的次数为7+5+8=20.因此他共测了20÷2=10(天).
三、17.解:(1)(2)如图所示.
(3)∠PQC=60°.
理由:因为 PQ∥CD,所以 ∠DCB+∠PQC=180°.
因为∠DCB=120°,所以∠PQC=180°-120°=60°.
18. 解:BE∥DF.
理由:因为AB∥CD,所以∠ABG=∠CDG .因为∠1=∠2,所以∠ABG-∠2=∠CDG-∠1,即∠EBG=∠FDG.所以BE∥DF.
19.解:因为∠BAC=120°,所以∠2+∠3=60°.①
因为∠1=∠2,所以∠4=∠3=∠1+∠2=2∠2.②
把②代入①,得3∠2=60°,所以∠2=20°. 所以∠1=∠2=20°.
所以∠DAC=∠BAC-∠1=120°-20°=100°.
20. 解:⑴是 90?
⑵因为这个“智慧三角形”的“智慧角”为108°,所以另一个角为108?÷3=36?,第三个内角为180?-108?-36?=36?.即这个“智慧三角形”各个角的度数分别为108°,36°,36°.
21.解:⑴∠DBC+∠BCE-∠A=180?.
证明:∠DBC+∠BCE =180?-∠ABC+180°-∠ACB=360?-(∠ABC+∠ACB)=360°-(180°-∠A)=180°+∠A.
即∠DBC+∠BCE-∠A=180?.
⑵∠A+∠F=90?.
证明:因为BF和CF分别平分∠CBD和∠BCE,所以∠CBF=∠CBD,∠BCF=∠BCE.
所以∠CBF+∠BCF=(∠CBD+∠BCE).
因为∠CBF+∠BCF=180?-∠F,由(1)知,∠DBC+∠BCE=180?+∠A.
所以180?-∠F=∠CBF+∠BCF=(∠DBC+∠BCE)=(180?+∠A).所以∠A+∠F=90?.
B
A
1
2
图2
C
D
E
图1
3
2
D
C
B
A
1
A
B
C
D
2
1
图3
A
B
C
图6
D
2
b
1
a
3
图5
A
B
C
D
E
F
图4
图7
A
B
C
D
E
F
D'
C'
图9
1
2
A
B
C
D
E
F
图10
G
图11
A
B
D
E
C
图12
A
B
D
E
C
图13
F
第3页共4页
时间90分钟 满分120分
班级:_________姓名:__________得分:________
一、精心选一选(每小题4分,共32分)
1.下列命题是真命题的是( )
A.若a2=b2,则a=b
B.若∠1+∠2=90?,则∠1与∠2互余
C.若∠α与∠β是同位角,则∠α=∠β
D.若a⊥b,b⊥c,则a⊥c
2.下列命题中,是公理的是( )
A.等角的补角相等 B.内错角相等,两直线平行
C.两点之间线段最短 D.三角形的内角和等于180?
3.如图1,下列条件能判定AB∥CD的是( )
A.∠1+∠2=180? B.∠3=∠2
C.∠2=∠1 D.∠1+∠3=180?
4.如图2,已知AB∥CD,能得到∠1=∠2的依据是( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
5.已知在△ABC中,∠A,∠B的外角分别是120?,150?,则∠C等于( )
A.60? B.90?
C.120? D.150?
6.下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A.a=-3 B.a=-1
C.a=1 D.a=3
7.如图3,已知∠2是△ABC的一个外角,那么∠2与∠B+∠1的大小关系是( )
A.∠2>∠B+∠1 B.∠2=∠B+∠1
C.∠2<∠B+∠1 D.无法确定
8.现有甲、乙、丙、丁、戊五个同学,他们分别来自一中、二中、三中.已知:①每所学校至少有他们中的一名学生;②在二中联欢会上,甲、乙、戊作为被邀请的客人演奏了小提琴;③乙过去曾在三中学习,后来转学了,现在同丁在同一个班学习;④丁、戊是同一所学校的三好学生.根据以上叙述可以断定甲所在的学校为( )
A.三中 B.二中
C.一中 D.不能确定
二、细心填一填(每小题4分,共32分)
9.把命题“直角三角形的两锐角互余”改写成“如果……那么……”的形式是 .
10.如图4所示,添加一个条件 ,可使AC∥DE.
11.如图5,已知直线a∥b,小杜把直角三角尺的直角顶点放在直线b上,若∠1=18°,则∠3的度数为____________.
12.如图6,点D为BC延长线上的一点,∠A=∠ACB,∠A=2∠B,则∠ACD的度数为 .
13.下列几个命题:①若两个实数相等,则它们的平方相等;②若三角形的三边长a,b,c满足(a-b)(a+b)+c2=0;则这个三角形是直角三角形;③有两边和一角分别相等的两个三角形全等.其中是假命题的有_________(填序号).
14.如图7,把一个长方形ABCD纸片沿EF折叠后,点D,C分别落在D',C'的位置,若∠AED'=30?, 则∠CFE=_____________°.
如图8,把一块含有30°角(∠A=30°)的直角三角尺ABC的直角顶点放在长方形桌面CDEF(CD∥EF)的一个顶点C处,桌面的另一个顶点F与三角尺斜边相交于点F,如果∠1=40°,那么∠AFE=________°.
图8
16.小明同学连续观察了太原市2014年8月份某几天的天气情况,他的观察结果是:①共有5个下午是晴天;②共有7个上午是晴天;③共有8个半天是雨天;④下午下雨的那天上午是晴天,则该学生观察的天数为_________.
三、耐心做一做(共56分)
17.(10分)读句画图:如图9,直线CD与直线AB相交于点C,
根据下列语句画图:
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由.
18.(10分)如图10,已知点B,D,G在同一条直线上,AB∥CD,∠1=∠2,请问BE与DF平行吗?为什么?
19.(10分)已知:如图11,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.
20.(12分)阅读理解:如果三角形满足一个角α是另一个角β的3倍时,那么我们称这个三角形为“智慧三角形”.其中α称为“智慧角”.
解答问题:
一个角为60?的直角三角形 (填“是”或“不是”)“智慧三角形”,若是,“智慧角”是 .
⑵已知一个“智慧三角形”的“智慧角”为108°,求这个“智慧三角形”各个角的度数.
21.(14分)数学活动课上,老师提出了一个问题:
我们知道,三角形的一个外角等于和它不相邻的两个内角的和,那么三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系?
(1)独立思考,请你完成老师提出的问题:
如图12所示,已知∠DBC和∠BCE分别为△ABC的两个外角,试探究∠A和∠DBC,∠BCE之间的数量关系.
解:
⑵合作交流,“创新小组”受此问题的启发:分别作外角∠CBD和∠BCE的平分线BF和CF,交于点F(如图13所示),那么∠A与∠F之间有何数量关系?请写出解答过程.
第八章 平行线的有关证明综合测评(一)参考答案
一、1.B 2.C 3.C 4.C 5.B 6.A 7.A 8.A
二、9.如果一个三角形是直角三角形,那么这个三角形的两锐角互余 10.答案不唯一,如∠A=∠BDE
11.72? 12.108? 13. ③ 14.105 15.10
16.10天 提示:由题意知,小明同学每天测两次,共测的次数为7+5+8=20.因此他共测了20÷2=10(天).
三、17.解:(1)(2)如图所示.
(3)∠PQC=60°.
理由:因为 PQ∥CD,所以 ∠DCB+∠PQC=180°.
因为∠DCB=120°,所以∠PQC=180°-120°=60°.
18. 解:BE∥DF.
理由:因为AB∥CD,所以∠ABG=∠CDG .因为∠1=∠2,所以∠ABG-∠2=∠CDG-∠1,即∠EBG=∠FDG.所以BE∥DF.
19.解:因为∠BAC=120°,所以∠2+∠3=60°.①
因为∠1=∠2,所以∠4=∠3=∠1+∠2=2∠2.②
把②代入①,得3∠2=60°,所以∠2=20°. 所以∠1=∠2=20°.
所以∠DAC=∠BAC-∠1=120°-20°=100°.
20. 解:⑴是 90?
⑵因为这个“智慧三角形”的“智慧角”为108°,所以另一个角为108?÷3=36?,第三个内角为180?-108?-36?=36?.即这个“智慧三角形”各个角的度数分别为108°,36°,36°.
21.解:⑴∠DBC+∠BCE-∠A=180?.
证明:∠DBC+∠BCE =180?-∠ABC+180°-∠ACB=360?-(∠ABC+∠ACB)=360°-(180°-∠A)=180°+∠A.
即∠DBC+∠BCE-∠A=180?.
⑵∠A+∠F=90?.
证明:因为BF和CF分别平分∠CBD和∠BCE,所以∠CBF=∠CBD,∠BCF=∠BCE.
所以∠CBF+∠BCF=(∠CBD+∠BCE).
因为∠CBF+∠BCF=180?-∠F,由(1)知,∠DBC+∠BCE=180?+∠A.
所以180?-∠F=∠CBF+∠BCF=(∠DBC+∠BCE)=(180?+∠A).所以∠A+∠F=90?.
B
A
1
2
图2
C
D
E
图1
3
2
D
C
B
A
1
A
B
C
D
2
1
图3
A
B
C
图6
D
2
b
1
a
3
图5
A
B
C
D
E
F
图4
图7
A
B
C
D
E
F
D'
C'
图9
1
2
A
B
C
D
E
F
图10
G
图11
A
B
D
E
C
图12
A
B
D
E
C
图13
F
第3页共4页
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
