华师大版八下数学18.2平行四边形的判定定理(2)课件(27张ppt)
文档属性
| 名称 | 华师大版八下数学18.2平行四边形的判定定理(2)课件(27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 617.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-13 07:33:40 | ||
图片预览





文档简介
课件27张PPT。HS八(下)
教学课件第18章 平行四边形18.2 平行四边形的判定第2课时 平行四边形的判定定理31.利用对角线互相平分判定平行四边形.(重点)2.综合应用平行四边形的性质与判定解决实际问
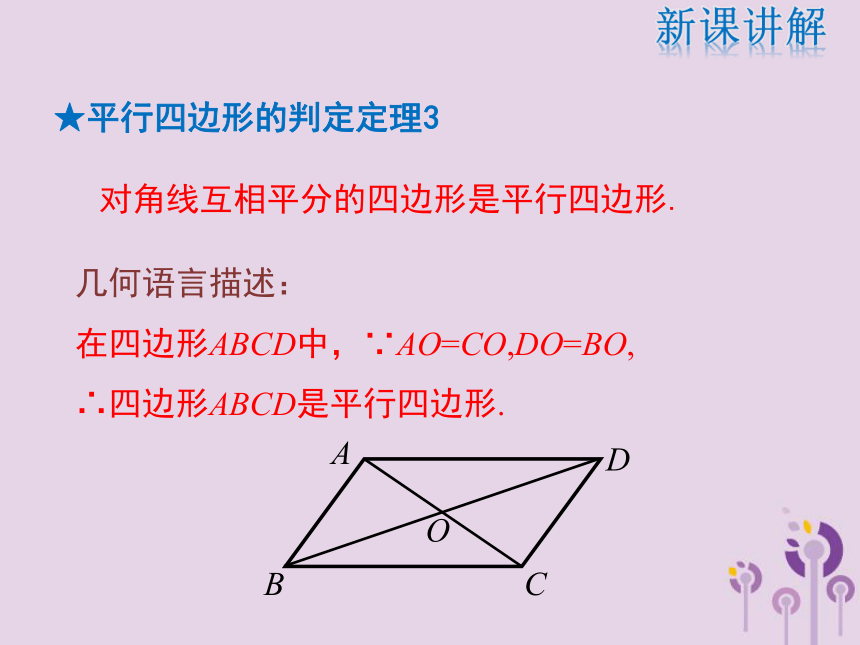
题.(难点)学习目标平行四边形的对角相等.平行四边形的对角线互相平分.两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.复习引入 如图,将两根细木条AC、BD的中点重叠,用小钉固定在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,四边形ABCD一直是一个平行四边形吗?BDOAC猜想:四边形ABCD一直是一个平行四边形. 你能根据平行四边形的定义证明它们吗?新课讲解平行四边形的判定定理3已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边 形ABCD是平行四边形.证明:在△AOB和△COD中,OA=OC (已知),OB=OD (已知),∠AOB=∠COD (对顶角相等),∴△AOB≌△COD(SAS),∴ ∠BAO=∠OCD ,∴AB∥ CD , ∴四边形ABCD是平行四边形.同理可证AD∥ BC新课讲解对角线互相平分的四边形是平行四边形.几何语言描述:
在四边形ABCD中,∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
新课讲解★平行四边形的判定定理3 如图, □ABCD 的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形. 证明:∵四边形ABCD是平行四边形,∴ AO=CO,BO=DO.∵AE=CF ,∴ AO-AE=CO-CF,即EO=OF.又∵BO=DO,∴四边形BFDE是平行四边形.新课讲解例11.根据下列条件,不能判定四边形为平行四边形的是
( )
A.两组对边分别相等 B.两条对角线互相平分
C.两条对角线相等 D.两组对边分别平行2.如图,在四边形ABCD中,AC与BD交于点O.如果AC=8cm,BD=10cm,那么当AO=_____cm,
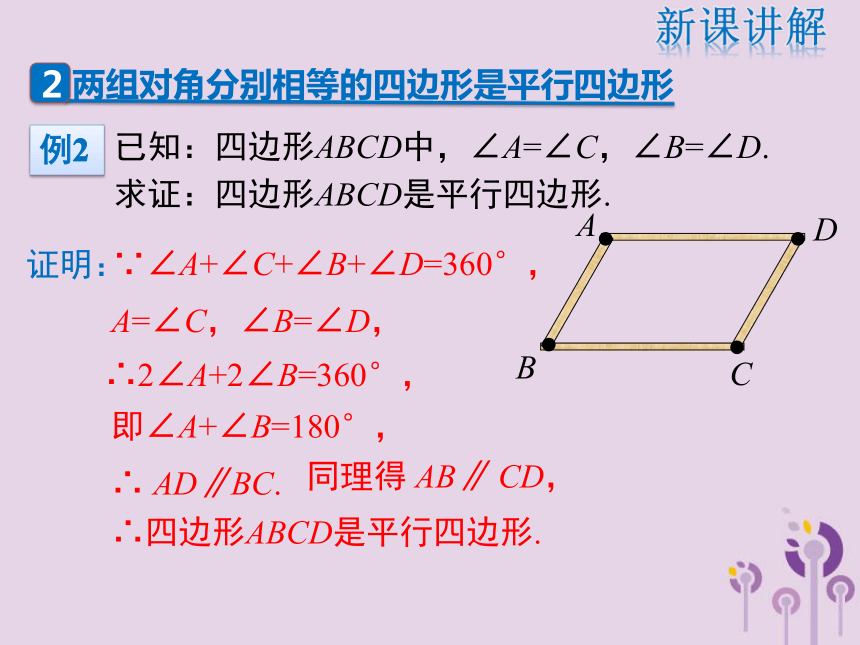
BO=_____cm时,四边形ABCD是平行四边形.C45新课讲解 已知:四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.A=∠C,∠B=∠D,∵∠A+∠C+∠B+∠D=360°,∴2∠A+2∠B=360°,即∠A+∠B=180°,∴ AD∥BC.∴四边形ABCD是平行四边形.同理得 AB∥ CD,证明:新课讲解两组对角分别相等的四边形是平行四边形例2两组对角分别相等的四边形是平行四边形.几何语言描述:
在四边形ABCD中,∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
新课讲解★平行四边形的判定定理 如图,四边形ABCD中,AB∥DC,∠B=55°,
∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°.
新课讲解例3(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形. 如图,四边形ABCD中,AB∥DC,∠B=55°,
∠1=85°,∠2=40°.
(2)求证:四边形ABCD是平行四边形.例31.判断下列四边形是否为平行四边形:是不是2.能判定四边形ABCD是平行四边形的条件:
∠A:∠B:∠C:∠D的值为 ( )A. 1:2:3:4 B. 1:4:2:3 C. 1:2:2:1 D. 3:2:3:2 D新课讲解 卢师傅要做一个平行四边形木框.他要从图中几根木条中选出四根来制作,可是他不知道该怎样选,请同学们帮他选一选,哪四根木条可以制作成平行四边形木框,为什么?7cm4cm3cm3cm5cm4cm新课讲解阅读与思考4cm4cm4cm4cm3cm3cm3cm3cm发现:一组对边平行,另一组对边相等的四边形不一定是平行四边形.两组边相等的四边形也不一定是平行四边形.3cm4cm4cm7cm新课讲解从边考虑两组对边分别平行的四边形是平行四边形(定义法)一组对边平行且相等的四边形是平行四边形(判定定理2)两组对边分别相等的四边形是平行四边形(判定定理1)从角考虑从对角线考虑平行四边形的判定方法两组对角分别相等的四边形是平行四边形(定义拓展)对角线互相平分的四边形是平行四边形(判定定理3)★平行四边形的判定方法总结新课讲解证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC.
∴AD BC.
∴四边形ABCD是平行四边形. 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.平行四边形的性质与判定的综合应用例4新课讲解 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个 B.1个 C.2个 D.3个 例5新课讲解解析:由平行四边形的判定方法可知:若是四边形的对角线互相平分,可证明这个四边形是平行四边形,②不能证明对角线互相平分,只有①③④可以,故选B.新课讲解如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD的中点.求证:
(1)△AOC≌△BOD;
(2)四边形AFBE是平行四边形.新课讲解证明:(1)∵AC∥BD,
∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO ,
∴△AOC≌△BOD(AAS).
(2)∵△AOC≌△BOD,
∴CO=DO.
∵E、F分别是OC、OD的中点,
∴EO=FO.
又∵AO=BO,
∴四边形AFBE是平行四边形.新课讲解1.判断对错.
(1)有一组对边平行的四边形是平行四边形. ( )
(2)有两条边相等,并且另外的两条边也相等的四边
形一定是平行四边形. ( )
(3)对角线互相平分的四边形是平行四边形. ( )
(4)一条对角线平分另一条对角线的四边形是平行四
边形. ( )
(5)有一组对角相等且一组对边平行的四边形是平行
四边形. ( ) √×××√随堂即练2.如图,四边形ABCD的对角线交于点O,下列哪组
条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD B随堂即练3.如图,五边形ABCDE是正五边形,连结BD、CE,
交于点P. 求证:四边形ABPE是平行四边形.证明:∵五边形ABCDE是正五边形,
∴正五边形的每个内角的度数是
AB=BC=CD=DE=AE,
∴∠DEC=∠DCE= ×(180°-108°)=36°,
同理∠CBD=∠CDB=36°,
∴∠ABP=∠AEP=108°-36°=72°,
∴∠BPE=360°-108°-72°-72°=108°=∠A,
∴四边形ABPE是平行四边形.随堂即练4.如图,△ABC中,AB=AC=10,D是BC边上的任意
一点,分别作DF∥AB交AC于点F,DE∥AC交AB
于点E,求DE+DF的值.解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF.
又∵AB=AC=10,
∴∠B=∠C.
∵DF∥AB,
∴∠CDF=∠B,
∴∠CDF=∠C,
∴DF=CF,
∴DE+DF=AF+FC=AC=10.随堂即练从边考虑两组对边分别平行的四边形是平行四边形(定义法)一组对边平行且相等的四边形是平行四边形(判定定理2)两组对边分别相等的四边形是平行四边形(判定定理1)从角考虑从对角线考虑平行四边形的判定方法两组对角分别相等的四边形是平行四边形(定义拓展)对角线互相平分的四边形是平行四边形(判定定理3)课堂总结
教学课件第18章 平行四边形18.2 平行四边形的判定第2课时 平行四边形的判定定理31.利用对角线互相平分判定平行四边形.(重点)2.综合应用平行四边形的性质与判定解决实际问
题.(难点)学习目标平行四边形的对角相等.平行四边形的对角线互相平分.两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.复习引入 如图,将两根细木条AC、BD的中点重叠,用小钉固定在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两根木条,四边形ABCD一直是一个平行四边形吗?BDOAC猜想:四边形ABCD一直是一个平行四边形. 你能根据平行四边形的定义证明它们吗?新课讲解平行四边形的判定定理3已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边 形ABCD是平行四边形.证明:在△AOB和△COD中,OA=OC (已知),OB=OD (已知),∠AOB=∠COD (对顶角相等),∴△AOB≌△COD(SAS),∴ ∠BAO=∠OCD ,∴AB∥ CD , ∴四边形ABCD是平行四边形.同理可证AD∥ BC新课讲解对角线互相平分的四边形是平行四边形.几何语言描述:
在四边形ABCD中,∵AO=CO,DO=BO,
∴四边形ABCD是平行四边形.
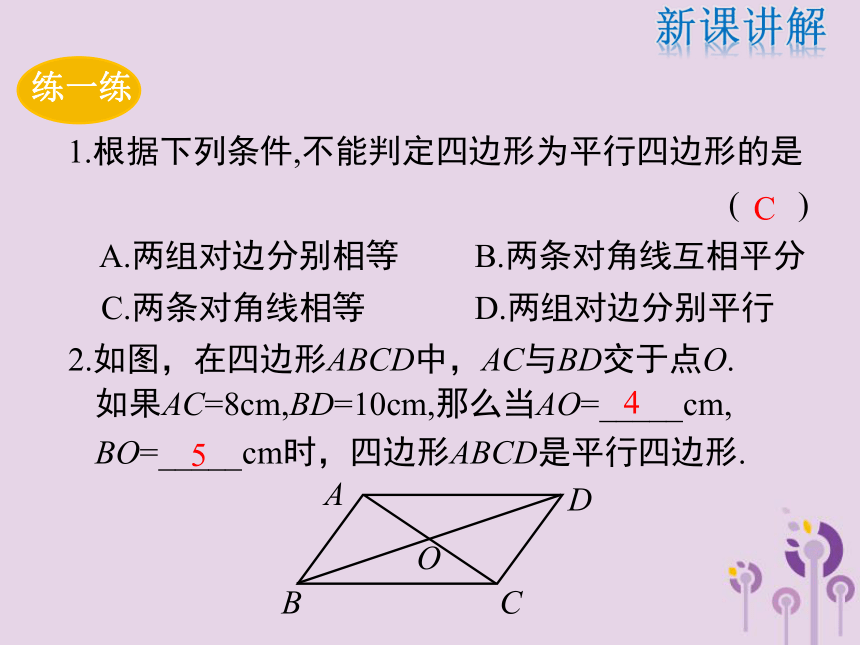
新课讲解★平行四边形的判定定理3 如图, □ABCD 的对角线AC、BD相交于点O,E、F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形. 证明:∵四边形ABCD是平行四边形,∴ AO=CO,BO=DO.∵AE=CF ,∴ AO-AE=CO-CF,即EO=OF.又∵BO=DO,∴四边形BFDE是平行四边形.新课讲解例11.根据下列条件,不能判定四边形为平行四边形的是
( )
A.两组对边分别相等 B.两条对角线互相平分
C.两条对角线相等 D.两组对边分别平行2.如图,在四边形ABCD中,AC与BD交于点O.如果AC=8cm,BD=10cm,那么当AO=_____cm,
BO=_____cm时,四边形ABCD是平行四边形.C45新课讲解 已知:四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.A=∠C,∠B=∠D,∵∠A+∠C+∠B+∠D=360°,∴2∠A+2∠B=360°,即∠A+∠B=180°,∴ AD∥BC.∴四边形ABCD是平行四边形.同理得 AB∥ CD,证明:新课讲解两组对角分别相等的四边形是平行四边形例2两组对角分别相等的四边形是平行四边形.几何语言描述:
在四边形ABCD中,∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
新课讲解★平行四边形的判定定理 如图,四边形ABCD中,AB∥DC,∠B=55°,
∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.(1)解:∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=55°.
新课讲解例3(2)证明:∵AB∥DC,
∴∠2=∠CAB,
∴∠DAB=∠1+∠2=125°.
∵∠DCB+∠DAB+∠D+∠B=360°,
∴∠DCB=∠DAB=125°.
又∵∠D=∠B=55°,
∴四边形ABCD是平行四边形. 如图,四边形ABCD中,AB∥DC,∠B=55°,
∠1=85°,∠2=40°.
(2)求证:四边形ABCD是平行四边形.例31.判断下列四边形是否为平行四边形:是不是2.能判定四边形ABCD是平行四边形的条件:
∠A:∠B:∠C:∠D的值为 ( )A. 1:2:3:4 B. 1:4:2:3 C. 1:2:2:1 D. 3:2:3:2 D新课讲解 卢师傅要做一个平行四边形木框.他要从图中几根木条中选出四根来制作,可是他不知道该怎样选,请同学们帮他选一选,哪四根木条可以制作成平行四边形木框,为什么?7cm4cm3cm3cm5cm4cm新课讲解阅读与思考4cm4cm4cm4cm3cm3cm3cm3cm发现:一组对边平行,另一组对边相等的四边形不一定是平行四边形.两组边相等的四边形也不一定是平行四边形.3cm4cm4cm7cm新课讲解从边考虑两组对边分别平行的四边形是平行四边形(定义法)一组对边平行且相等的四边形是平行四边形(判定定理2)两组对边分别相等的四边形是平行四边形(判定定理1)从角考虑从对角线考虑平行四边形的判定方法两组对角分别相等的四边形是平行四边形(定义拓展)对角线互相平分的四边形是平行四边形(判定定理3)★平行四边形的判定方法总结新课讲解证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC.
∴AD BC.
∴四边形ABCD是平行四边形. 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.平行四边形的性质与判定的综合应用例4新课讲解 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,E、F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.0个 B.1个 C.2个 D.3个 例5新课讲解解析:由平行四边形的判定方法可知:若是四边形的对角线互相平分,可证明这个四边形是平行四边形,②不能证明对角线互相平分,只有①③④可以,故选B.新课讲解如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD的中点.求证:
(1)△AOC≌△BOD;
(2)四边形AFBE是平行四边形.新课讲解证明:(1)∵AC∥BD,
∴∠C=∠D.
又∵∠COA=∠DOB,AO=BO ,
∴△AOC≌△BOD(AAS).
(2)∵△AOC≌△BOD,
∴CO=DO.
∵E、F分别是OC、OD的中点,
∴EO=FO.
又∵AO=BO,
∴四边形AFBE是平行四边形.新课讲解1.判断对错.
(1)有一组对边平行的四边形是平行四边形. ( )
(2)有两条边相等,并且另外的两条边也相等的四边
形一定是平行四边形. ( )
(3)对角线互相平分的四边形是平行四边形. ( )
(4)一条对角线平分另一条对角线的四边形是平行四
边形. ( )
(5)有一组对角相等且一组对边平行的四边形是平行
四边形. ( ) √×××√随堂即练2.如图,四边形ABCD的对角线交于点O,下列哪组
条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD B随堂即练3.如图,五边形ABCDE是正五边形,连结BD、CE,
交于点P. 求证:四边形ABPE是平行四边形.证明:∵五边形ABCDE是正五边形,
∴正五边形的每个内角的度数是
AB=BC=CD=DE=AE,
∴∠DEC=∠DCE= ×(180°-108°)=36°,
同理∠CBD=∠CDB=36°,
∴∠ABP=∠AEP=108°-36°=72°,
∴∠BPE=360°-108°-72°-72°=108°=∠A,
∴四边形ABPE是平行四边形.随堂即练4.如图,△ABC中,AB=AC=10,D是BC边上的任意
一点,分别作DF∥AB交AC于点F,DE∥AC交AB
于点E,求DE+DF的值.解:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴DE=AF.
又∵AB=AC=10,
∴∠B=∠C.
∵DF∥AB,
∴∠CDF=∠B,
∴∠CDF=∠C,
∴DF=CF,
∴DE+DF=AF+FC=AC=10.随堂即练从边考虑两组对边分别平行的四边形是平行四边形(定义法)一组对边平行且相等的四边形是平行四边形(判定定理2)两组对边分别相等的四边形是平行四边形(判定定理1)从角考虑从对角线考虑平行四边形的判定方法两组对角分别相等的四边形是平行四边形(定义拓展)对角线互相平分的四边形是平行四边形(判定定理3)课堂总结
