21.3.1 方差 教案(表格式)
文档属性
| 名称 | 21.3.1 方差 教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 282.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-16 00:00:00 | ||
图片预览


文档简介
课 题
21.3.1方差
课 型
新授课
节数
1
备课人
审核人
授课人
日期
教
学
目
标
知识与技能
理解极差,方差、标准差的意义
过程与方法
会计算一组数据的极差,方差和标准差
情感态度
激发学生解决的愿望,能利用极差,方差和标准差解决一些简单的实际问题
教材
分析
重点
计算一组数据的极差,方差和标准差
难点
利用极差,方差和标准差解决实际问题
教学
模式
三疑三探
课时
共_2_课时
学法
自学 合作 探究
主 案
副案(修改栏)
一、设疑自探(10分钟)
(一)创设情境,导入新课
一)新授
创设意境
小明初一时对数学不感兴趣,遇到问题不爱动脑筋,作业能做就做,不会做就不做,因此他的数学成绩不太好,初一的一学年中四次考试的数学成绩分别是75、78、77、76.初一暑假时,小明参加了科技活动小组,在活动中,小明体会到学好数学的重要性,逐渐对数学产生了兴趣,遇到问题时从多方面去思考,深入钻研.因此小明的数学成绩进步很快,初二的一学年中,小明在四次考试的数学成绩是80、85、92、95. 看完这则小通讯,请谈谈你的看法.你以为在这些数据中最能反映学习态度重要性的是哪一对数据?两者相差多少?
相比较而言最能反映学习兴趣重要性的是初一时的75分和初二时的95分,两者相差达20分.这个20分在数学上就称为极差.
(二)根据课题,提出问题。看到这个课题,你想知道什么?请提出来,预设:
同学们提出的问题真好,大多都是我们本节应该学习的知识,老师将大家提出的问题归纳、整理,补充为下面的自探提示,希望能对大家本节的学习提供帮助。
(三)出示自探提示,组织学生自探。( 分钟)自探提示:
1.看看课本 ,边看边想边思。
2.对于重要地方划一划,不懂的地方做标记,讲的时候认真听。
二、解疑合探( 分钟)
(一).小组合探。
1.小组内讨论解决自探中未解决的问题;
2.教师出示展示与评价分工。
问题
展示
评价
(二).全班合探。
1.学生展示与评价;
2.教师点拨或精讲。
学生展示与评价;
问题1
该表显示:上海2001年2月下旬和2002年同期的每日最高气温
2月21日
2月22日
2月23日
2月24日
2月25日
2月26日
2月27日
2月28日
2001年
12
13
14
22
6
8
9
12
2002年
13
13
12
9
11
16
2
10
问: 2001年2月下旬上海的气温的极差是多少?
2002年同期的上海的气温的极差又是多少?
结论: 2001年的2月下旬的气温变化幅度大于2002年同期的变化幅度.
经计算可以看出,对于2月下旬的这段时间而言, 2001年和2002年上海地区的平均气温相等,都是12。C.这是不是说,两个时段的气温情况没有差异呢?
思考:
什么样的指标可以反映一组数据变化范围的大小?
我们可以用一组数据中的最大值减去最小值所得的差来反映这组数据的变化范围.用这种方法得到的差称为极差(range)
极差=最大值-最小值.
在生活中,我们常常会和极差打交道.班级里个子最高的学生比个子最矮的学生高多少?家庭中年纪最大的长辈比年纪最小的孩子大多少?这些都是求极差的例子.
极差是最简单的一种度量数据波动情况的量,但只能反映数据的波动范围,不能衡量每个数据的变化情况,而且受极端值的影响较大.
思考
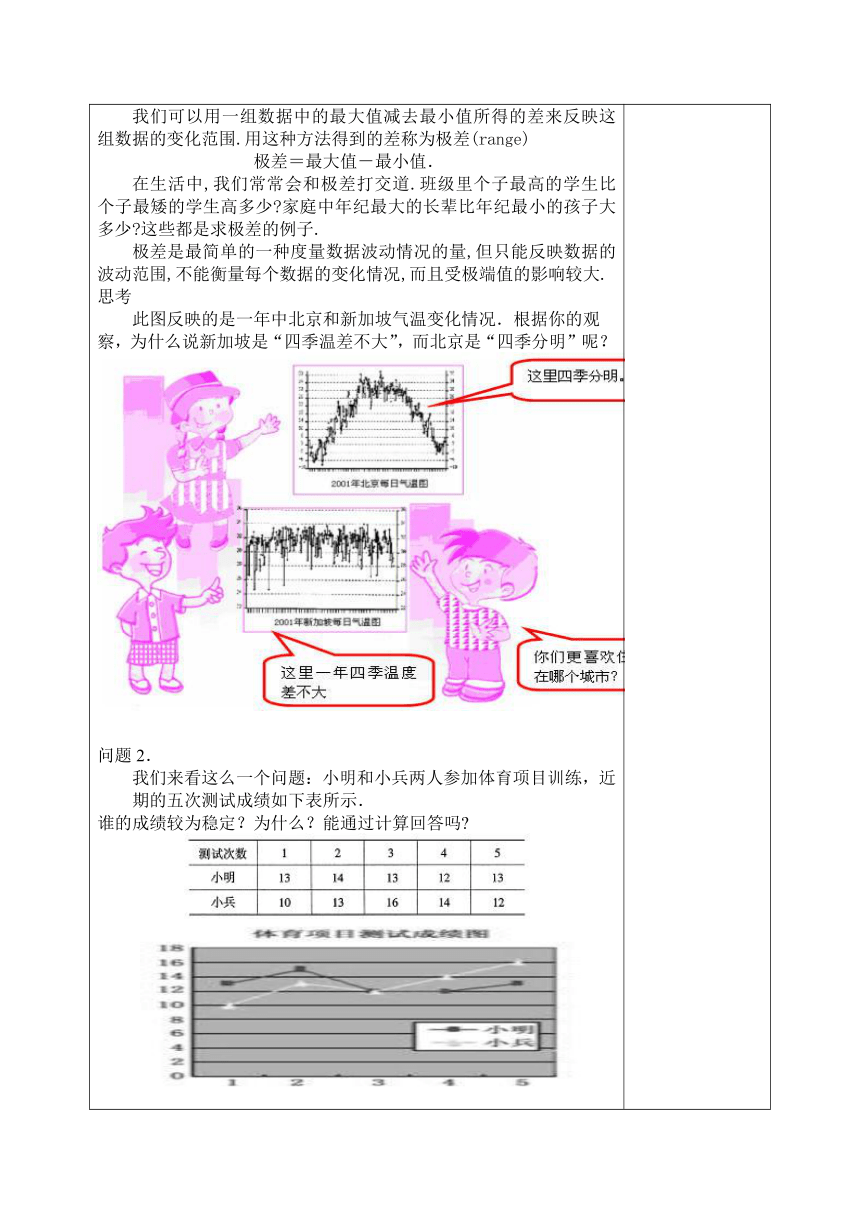
此图反映的是一年中北京和新加坡气温变化情况.根据你的观察,为什么说新加坡是“四季温差不大”,而北京是“四季分明”呢?
问题2.
我们来看这么一个问题:小明和小兵两人参加体育项目训练,近期的五次测试成绩如下表所示.
谁的成绩较为稳定?为什么?能通过计算回答吗?
由计算可知,两人测试成绩的平均值都是13分.但相比之下,小明的成绩大部分集中在13分附近,而小兵的成绩与其平均值的离散程度较大.通常,如果一组数据与其平均值的离散程度较小,我们就说它比较稳定.请同学们根据上表提供的数据画出折线图(与上图作比较).
请同学们进一步思考,什么样的数能反映一组数据与其平均值的离散程度? 从表和图中可以看到,小兵的测试成绩与平均值的偏差较大,而小明的较小.那么如何加以说明呢?可以直接将各数据与平均值的差进行累加吗?在下表中写出你的计算结果并进行小结,可以用它来比较两组数据围绕其平均值的波动情况(离散程度)吗?(给同学们足够的时间计算和讨论)
对于 每次成绩-平均成绩 求和的结果为零(请同学们说说为什么?).那么,你能提出一个可行的方案吗?请在下表的红色格子中写上新的计算方案,并将计算结果填入表中.
(部分学生可能提出求差后求绝对值再求和的方法等,要多肯定和比较,引导学生共同导出方差的计算公式)
考虑实际情况,如果一共进行了7次测试,小明因故缺席两次,怎样比较谁的成绩更稳定?请将你的方法与数据填入下表中.
(通过两张表格的对比让学生进一步明白:为什么要用“每次成绩”和“平均成绩”相减;为什么要“平方”;为什么求“平均数”比“求和”好.)
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况.这个结果通常称为方差(variance).公式为
方差越大,说明这组数据偏离平均值的情况越严重,即离散程度较大,数据也越不稳定. 我们通常用S 2表示一组数据的方差,用表示一组数据的平均数,x1、x2、… 表示各个数据.上面问题中方差的计算式就是
从方差的计算过程,可以看出S 2 的数量单位与原数据的不一致,因此在实际应用时常常将求出的方差再开平方,这就是标准差(standard deviation),用符号表示为.
发现:
方差越小,波动越小.方差越大,波动越大.
质疑再探:( 分钟)
1.现在,我们已经解决了自探问题。下面我们再回看一下,开始我们提出的问题还有那些没有解决?
2.本节的知识已经学完,对于本节的学习,谁还有什么问题或不明白的地方?请提出来,大家一起来解决.
四、运用拓展( 分钟)
(一)根据本节学习内容,学生自编习题,交流解答。
请你来当小老师,编一道题,考考大家(同桌)!
根据学生自编习题的练习情况,教师有选择地出示下面的习题共学生练习。为了巩固本节知识,加强知识的运用拓展,老师也给大家设计了一些习题,检测一下大家对本节知识的掌握与运用情况,请看:
1.请计算刚才问题中小明和小兵五次测试成绩的极差、方差和标准差.
解: 小明和小兵五次测试成绩的极差分别为14-12=2和16-10=6.
小明和小兵五次测试成绩的方差分别为
(其中小明和小兵5次测试成绩的平均数都为13)
经过比较可知,小明的测试成绩较为稳定.
2.比较下列两组数据的极差、方差和标准差:
A组:0, 10, 5, 5, 5, 5, 5, 5, 5, 5;
B组:4, 6, 3, 7, 2, 8, 1, 9, 5, 5
解:求方差: A的方差﹤B的方差
(三)全课总结
1.学生谈学习收获。通过这节课的学习,你都有哪些收获?谈一谈.
1. 了解极差,方差和标准差的意义.
2. 知道极差,方差和标准差的计算方法.
3. 会利用极差,方差和标准差的计算结果来分析一组数据的离散程度
2.学科班长评价本节课活动情况。
板书设计
方差
1. 了解极差,方差和标准差的意义.
2. 知道极差,方差和标准差的计算方法.
3. 会利用极差,方差和标准差的计算结果来分析一组数据的离散程度 .
作业布置
课本P155习题20.3第1题
练习册对应章节
教 学反 思
