27.1.2 圆的对称性圆的认识 教案(表格式)
文档属性
| 名称 | 27.1.2 圆的对称性圆的认识 教案(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 63.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-16 08:15:20 | ||
图片预览


文档简介
课题
2.圆的对称性
课时
第1课时
上课时间
教学目标
1.知识与技能
(1)知道圆既是轴对称图形又是中心对称图形还是旋转对称图形.
(2)理解弧、弦和圆心角之间的关系定理及推论,并能解决相关问题的证明.
2.过程与方法
(1)在探究三弧、弦和圆心角之间的关系定理及推论的过程中,培养学生的动手操作和观察分析问题的能力.
(2)在运用相关定理和推论进行证明的过程中感受几何中推理的严谨性,培养学生的逻辑思维能力.
3.情感、态度与价值观
(1)通过对相关定理的探究感受数学知识的严谨性,培养科学的学习态度.
(2)在自主探究和分组讨论的过程中体会成功的快乐,增强学好数学的信心,感受合作的价值.
教学
重难点
重点:掌握弧、弦和圆心角之间的关系定理及推论,并能解决相关问题的证明.
难点:探究弧、弦和圆心角之间的关系定理及推论的思维过程.
教学活动设计
二次设计
课堂导入
思考下面的问题:
1.轴对称图形和中心对称图形的性质有哪些?
2.圆具有什么对称性?
3.在对圆进行旋转的过程中,比较前后的图形,你有什么发现?
探索新知
合作探究
自学指导
1.在圆形纸片上画出弧AB,连结弦AB,连结半径OA和OB得到圆心角∠AOB,将圆形纸片旋转一个角度后画出相应的部分进行观察.
2.分析圆心角相同时,所对的弦和弧有何关系;总结圆心角、弧和弦之间的关系定理及其推论.
3.教材例1中已知哪些弧相等?可以推出哪些弧相等?∠1与∠2有何关系?自己尝试证明例1.
4.自制一个圆形纸片,进行对折,观察分析圆的对称轴以及如何把圆2等分,4等分…….
5.自学课本P37~39,记住弧、弦和圆心角之间的关系定理及推论,并结合图形写出符号语言.
学生看书,教师巡视,老师督促每一位学生认真、紧张地自学,鼓励学生质疑问难.
合作探究
1.讨论
小组讨论自学指导中出现疑问的地方.
2.组织学生探究弧、弦和圆心角之间的关系.
3.组织学生探究弧、弦和圆心角之间的关系定理的推论.
4.组织学生结合例题探究弧、弦和圆心角之间的关系定理的推论的运用.
5.组织学生探究圆的对称性以及等分圆.
探索新知
合作探究
教师指导
1.易错点
(1)弄错弧弦以及圆心角的对应关系.
(2)在证明或计算的过程中,条件不充分,格式不规范.
2.归纳小结
(1)弧、弦和圆心角之间的关系定理及推论:弧相等?所对的弦相等?所对的弧相等.
(2)对称性:任意一条直径所对的直线都是圆的对称轴.
3.方法规律
(1)在同一个圆中弧可以进行等量加减.
(2)求角,先找角所对的弧,在找弧所对的其他角,进行转化.
当堂训练
1.如图,在☉O中,若点C是的中点,∠A=50°,则∠BOC= ?
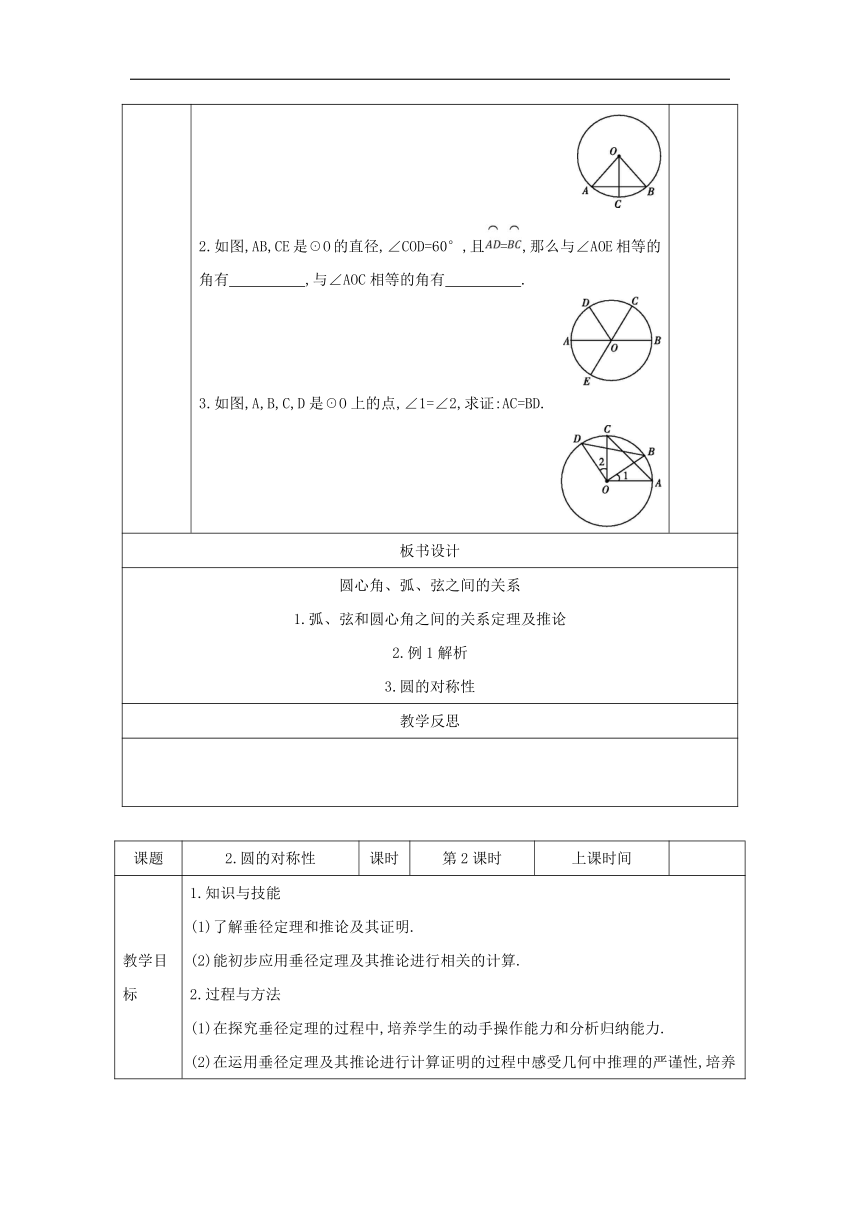
2.如图,AB,CE是☉O的直径,∠COD=60°,且=,那么与∠AOE相等的角有 ,与∠AOC相等的角有 .?
3.如图,A,B,C,D是☉O上的点,∠1=∠2,求证:AC=BD.
板书设计
圆心角、弧、弦之间的关系
1.弧、弦和圆心角之间的关系定理及推论
2.例1解析
3.圆的对称性
教学反思
课题
2.圆的对称性
课时
第2课时
上课时间
教学目标
1.知识与技能
(1)了解垂径定理和推论及其证明.
(2)能初步应用垂径定理及其推论进行相关的计算.
2.过程与方法
(1)在探究垂径定理的过程中,培养学生的动手操作能力和分析归纳能力.
(2)在运用垂径定理及其推论进行计算证明的过程中感受几何中推理的严谨性,培养学生的推理能力.
3.情感、态度与价值观
(1)通过在计算或证明中感受数学知识的严谨性,培养学生良好的学习习惯.
(2)在自主探究中体会成功的快乐,增强学好数学的信心,增强学习的兴趣.
教学
重难点
重点:运用垂径定理和推论进行简单的计算和证明.
难点:探究垂径定理和推论的思维过程.
教学活动设计
二次设计
课堂导入
思考下面的问题:
1.圆的对称轴是什么?
2.等腰三角形有哪些性质?
3.根据你对圆的认识,怎样可以在圆中构造等腰三角形?
探索新知
合作探究
自学指导
1.自己制作一个圆形纸片,对折画出直径,再任意画出一条与直径垂直的弦.
2.沿直径再次对折,结合教材图27.1.7观察分析AP与BP;与有何关系.
3.总结垂直于弦的直径与其所对的弦和弧之间有何联系: .?
4.根据命题画出图形,写出已知和求证,根据同一个圆的半径相等与等腰三角形的性质进行证明.
5.根据教材记住垂径定理: .?
6.分析垂径定理的推理,并类比垂径定理的证明加以论证.
7.自学课本P39~40,记住垂径定理及其推理,结合图形写出符号语言.
学生看书,教师巡视,老师督促每一位学生认真、紧张地自学,鼓励学生质疑问难.
合作探究
1.讨论
小组讨论自学指导中出现疑问的地方.
2.组织学生探究垂径定理.
3.组织学生探究垂径定理的推理.
4.组织学生结合例题探究垂径定理及其推理的运用.
教师指导
1.易错点
(1)在运用垂径定理的推论中忽略“不是直径”的条件.
(2)在证明或计算的过程中,条件不充分,格式不规范.
探索新知
合作探究
2.归纳小结
(1)垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.
(2)推论1:
推论2:
3.方法规律
(1)垂径定理的运用往往与勾股定理相结合,弦的一半、弦心距和半径围成一个直角三角形,满足勾股定理.
(2)当已知弧的中点时,往往连接半径运用垂径定理.
当堂训练
1.下列说法正确的是( )
(A)平分弦的直径垂直于弦
(B)垂直于弦的直线必过圆心
(C)垂直于弦的直径平分弦
(D)平分弦的直径平分弦所对的弧
2.如图,AB为☉O的直径,弦CD⊥AB,垂足为P,若OP=3,CD=8,则AO= .?
3.已知,如图,☉O的直径AB与弦CD相交于点E,AE=1,BE=5,∠AEC=45°,求CD的长.
板书设计
垂径定理
1.垂径定理
2.推论1
推论2
3.练习
教学反思
