6.1 正比例的意义课件苏教版(共25张PPT)
文档属性
| 名称 | 6.1 正比例的意义课件苏教版(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 263.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-15 17:57:34 | ||
图片预览






文档简介
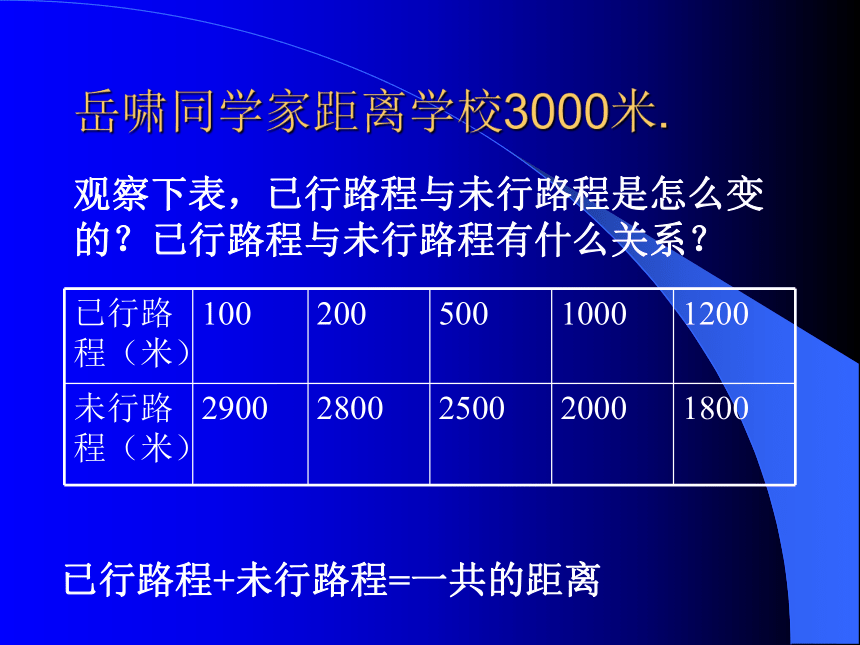
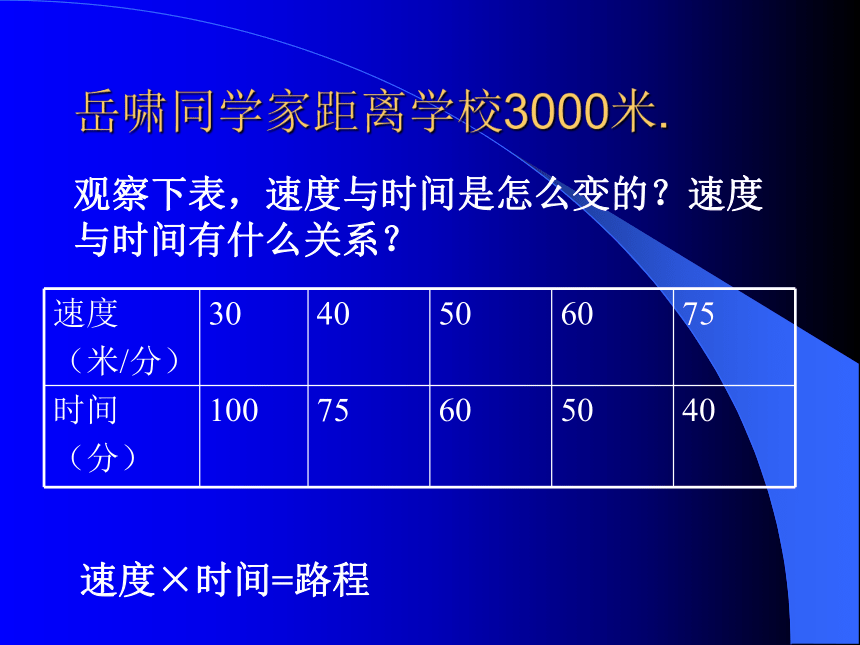
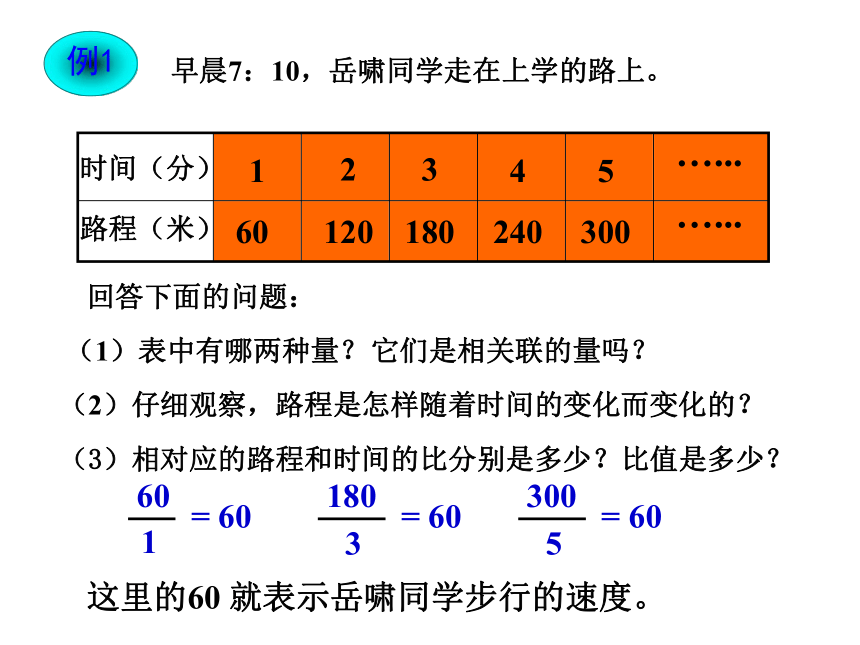
课件25张PPT。正比例的意义岳啸同学家距离学校3000米.观察下表,已行路程与未行路程是怎么变的?已行路程与未行路程有什么关系?已行路程+未行路程=一共的距离岳啸同学家距离学校3000米.观察下表,速度与时间是怎么变的?速度与时间有什么关系?速度×时间=路程一种量变化,另一种量也随着变化。像这样的两种量,一般我们称为两种相关联的量。你还能举出一些相关联的两个量吗?它们是相关联的量吗?考考你1、学校买《盐城晚报》,数量与总价2、老师的年龄和你的的数学成绩3、圆的周长和直径…...时间(分钟)路程(米)12560…...早晨7:10,岳啸同学走在上学的路上。(3)相对应的路程和时间的比分别是多少?比值是多少?时间(分)2345120180240300回答下面的问题:(1)表中有哪两种量?它们是相关联的量吗?(2)仔细观察,路程是怎样随着时间的变化而变化的?这里的60 就表示岳啸同学步行的速度。…...时间(分钟)总价(元)121.6…...星期六,高翔同学帮助蒋老师买红圆珠笔。数量(枝)23453.24.86.4 8这里的1.6就表示红圆珠笔的单价。观察例1、例2,你发现这两个例题有什么共同的地方吗?…...路程(米)160…...时间(分)2345120180240300…...总价(元)11.6…...数量(枝)23453.24.86.4 8在两个相关联的量中,一个量随着另一个量的变化而变化,在变化过程中,两个量的比值(也就是商)一定,我们就说这两个量是成正比例的量,它们的关系叫做正比例关系. =(一定) 路程和时间是两种相关联的量,时间变化,路程也随着变化。当路程和对应时间的比的比值总是一定(也就是速度一定)时,我们就说行驶的路程和时间成正比例,行驶的路程和时间是成正比例的量。总价和数量是两种相关联的量,数量变化,总价也随着变化。当总价和对应数量的比的比值总是一定(也就是单价一定)时,我们就说铅笔的总价和数量成正比例,铅笔的总价和数量是成正比例的量。 练一练:完成第57页练一练
这堂课你有哪些收获?你对自己的表现满意吗?温故而知新 六0五班的总人数一定,满意的人数和比较满意的人数成正比例吗?为什么?提问时间你还有什么关于正比例意义的问题要问吗?考考你1、是不是所有相关联的两种量都能成正比例?2、是不是所有成正比例的两种量都是相关联的量?练一练嘉兴民丰造纸厂的生产情况如下表,根据表回答问题时间和生产量是两种相关联的量,生产量时间=每天生产的吨数(一定)所以 生产量和时间成正比例.练一练总价数量=单价(一定)所以 购买苹果的数量和总价成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.(1)苹果的单价一定,购买苹果的数量和总价.苹果的数量和总价是两种相关联的量,练一练路程时间=速度(一定)所以 行驶的路程和时间成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.(2)轮船行驶的速度一定,行驶的路程和时间.行驶的路程和时间是两种相关联的量,练一练织布总米数时间=每小时织布米数(一定)所以 织布总米数和时间成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.(3)每小时织布米数一定,织布总米数和时间.织布总米数和时间是两种相关联的量,练一练所以高举盛跳高的高度和他的身高不成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.(4)高举盛跳高的高度和他的身高.跳高的高度和身高不是两种相关联的量,思考所以 正方形的周长和边长成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.正方形的周长和边长正方形的周长和边长是两种相关联的量,正方形周长边长= 4(一定)思考所以 正方形的面积和边长不成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.正方形的面积和边长正方形的面积和边长是两种相关联的量,正方形面积边长= 边长(不一定)边长面积11比值123424934165255……… 判断下面各题中的两种量是否成正比例。( 1) 神州6号在轨道上飞行的速度是一定的,
飞行的路程与飞行的时间。 ( )( 2) 长方形的长是一定的,它的宽与面积。 ( ) ( 3) 被减数一定,减数与差。 ( ) ( 4) 比例尺一定,图上距离与实际距离。 ( ) ( 5) 圆的周长与它的半径。 ( ) 做一做判断下面每题中的两种量是不是成正比例,并说明理由。1.每包书中册数相同,包数和总册数。
2.全班的学生人数一定,每组的人数和组数。
3.房间地面面积一定,房间里的人数和每人
所占的面积。
4.和一定,加数和另一个加数。
5.一个人的年龄和他的体重。思考圆形的面积和半径是不是成正比例,并说明理由.
这堂课你有哪些收获?你对自己的表现满意吗?温故而知新 六0五班的总人数一定,满意的人数和比较满意的人数成正比例吗?为什么?提问时间你还有什么关于正比例意义的问题要问吗?考考你1、是不是所有相关联的两种量都能成正比例?2、是不是所有成正比例的两种量都是相关联的量?练一练嘉兴民丰造纸厂的生产情况如下表,根据表回答问题时间和生产量是两种相关联的量,生产量时间=每天生产的吨数(一定)所以 生产量和时间成正比例.练一练总价数量=单价(一定)所以 购买苹果的数量和总价成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.(1)苹果的单价一定,购买苹果的数量和总价.苹果的数量和总价是两种相关联的量,练一练路程时间=速度(一定)所以 行驶的路程和时间成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.(2)轮船行驶的速度一定,行驶的路程和时间.行驶的路程和时间是两种相关联的量,练一练织布总米数时间=每小时织布米数(一定)所以 织布总米数和时间成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.(3)每小时织布米数一定,织布总米数和时间.织布总米数和时间是两种相关联的量,练一练所以高举盛跳高的高度和他的身高不成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.(4)高举盛跳高的高度和他的身高.跳高的高度和身高不是两种相关联的量,思考所以 正方形的周长和边长成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.正方形的周长和边长正方形的周长和边长是两种相关联的量,正方形周长边长= 4(一定)思考所以 正方形的面积和边长不成正比例. 判断下面每题中的两种量是不是成正比例,并
说明理由.正方形的面积和边长正方形的面积和边长是两种相关联的量,正方形面积边长= 边长(不一定)边长面积11比值123424934165255……… 判断下面各题中的两种量是否成正比例。( 1) 神州6号在轨道上飞行的速度是一定的,
飞行的路程与飞行的时间。 ( )( 2) 长方形的长是一定的,它的宽与面积。 ( ) ( 3) 被减数一定,减数与差。 ( ) ( 4) 比例尺一定,图上距离与实际距离。 ( ) ( 5) 圆的周长与它的半径。 ( ) 做一做判断下面每题中的两种量是不是成正比例,并说明理由。1.每包书中册数相同,包数和总册数。
2.全班的学生人数一定,每组的人数和组数。
3.房间地面面积一定,房间里的人数和每人
所占的面积。
4.和一定,加数和另一个加数。
5.一个人的年龄和他的体重。思考圆形的面积和半径是不是成正比例,并说明理由.
