2019年沪科版第八章压强计算综合复习(无答案)
文档属性
| 名称 | 2019年沪科版第八章压强计算综合复习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 744.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-06-16 21:13:47 | ||
图片预览


文档简介
压强计算专题
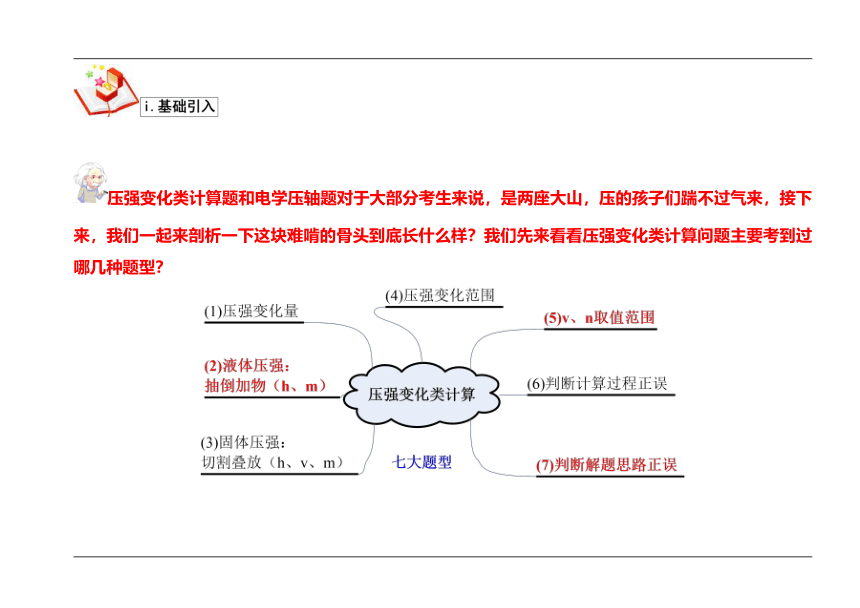
压强变化类计算题和电学压轴题对于大部分考生来说,是两座大山,压的孩子们踹不过气来,接下来,我们一起来剖析一下这块难啃的骨头到底长什么样?我们先来看看压强变化类计算问题主要考到过哪几种题型?
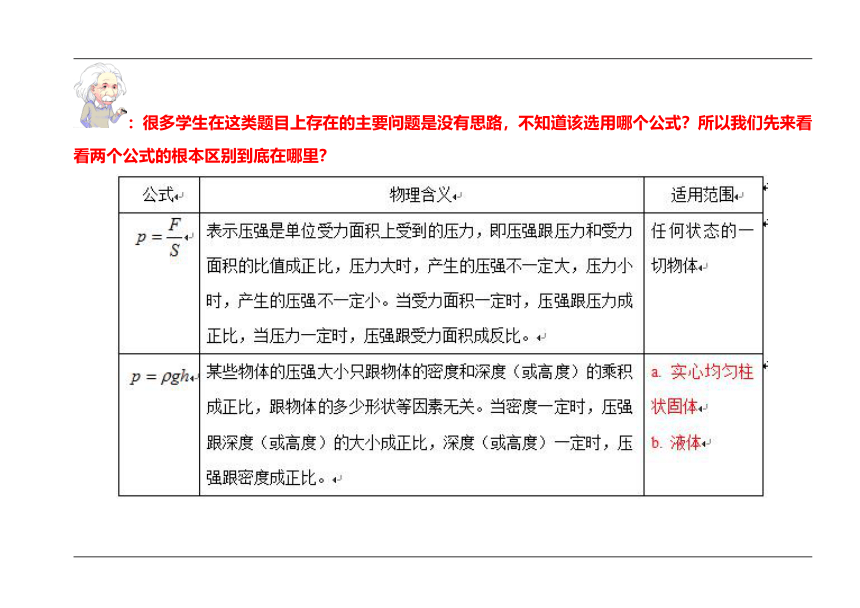
:很多学生在这类题目上存在的主要问题是没有思路,不知道该选用哪个公式?所以我们先来看看两个公式的根本区别到底在哪里?
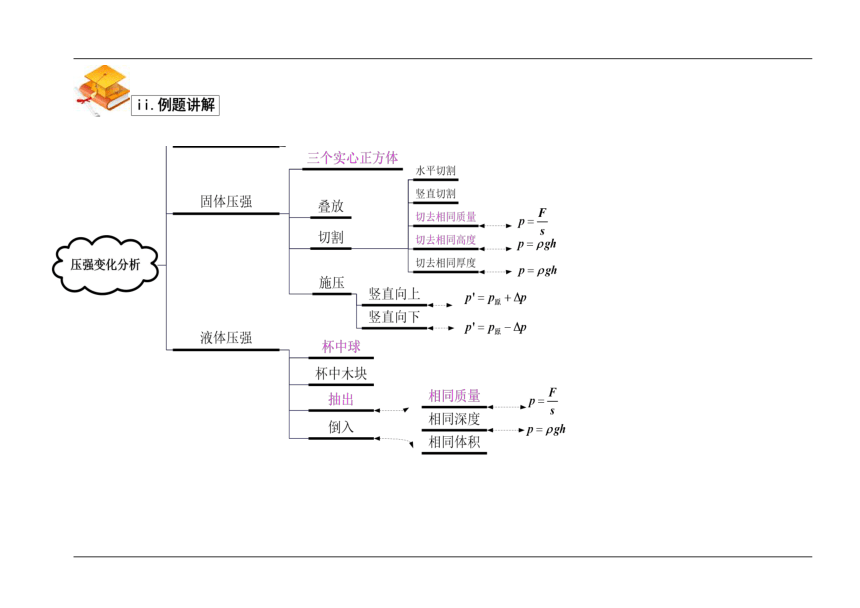
:接下来我们再来看看主要用到哪些知识点?
1、如图12所示,实心均匀正方体A、B放置在水平地面上,它们的重均为980牛,A的边长为0.25米,B的边长为0.4米。
①求正方体A的密度ρA
②求正方体B对水平地面的压强pB。
③若在正方体A、B上沿水平方向分别截去相同的体积ΔV后,A、B剩余部分对水平地面的压强pA?和pB?,请通过计算比较它们的大小关系及其对应的ΔV的取值范围。
2、如图14所示, 两个底面积大小分别为10厘米2和8厘米2的薄壁圆柱形容器A和B放置在水平桌面上,已知A容器内部液体甲对容器底部产生的压强为3136帕,B容器内部盛的液体乙是水,且两容器中的液体液面高度均为0.4米。
⑴求甲液体的密度ρ甲。
⑵求乙液体(水)对B容器底部的压力F乙
⑶若再从A、B两容器内同时抽出体积(ΔV)相等的液体后,甲乙两种液体对容器底部的压强分别为p?甲和p?乙,请通过计算比较它们的大小关系及其对应的ΔV的取值范围。
3、底面积为1×102米2的轻质柱形容器中盛有0.1米深的水,放在水平桌面中央。将体积为2×104米3、质量为1千克的球形物体浸没在水中后,物体沉入容器底部,水未溢出。求:
① 未放入物体时水对容器底部的压强p水。
② 放入物体后容器对桌面的压力F容器。
③ 放入物体后水对容器底部压强的增加量△p。
4、水平地面上有一个质量为1千克、底面积为2×102米2的薄壁圆柱形容器,容器内盛有体积为5×103米3的水。
① 求容器中水的质量。
② 求容器对地面的压强。
③ 现将一质量为0.2千克的物块浸在水中,求容器对水平地面压强的最大增加量。
5、一个底面积为2102米2的薄壁圆柱形容器放在水平桌面中央,容器高为0.12米,内盛有0.1米深的水,如图14(a)所示,另有质量为2千克,体积为1103米3的实心正方体A,如图14(b)所示,求:
(1)图14(a)中水对容器底部的压强。
(2)图14(b)实心正方体A的密度。
(3)将实心正方体A放入图14(a)的水中后,水面上升的高度。
6、水平地面上有一个质量为1千克、底面积为1x10-2米2的薄壁圆柱形容器,容器内盛有质量为4千克的水。
① 求水的体积V。
② 求容器对地面的压强p。
③ 现将一物块浸没在水中,水未溢出,若容器对地面压强的增加量等于水对容器底部压强的增加量,则该物块的密度为 千克/米3。
7、质量为2千克、底面积为0.02米2的薄壁圆柱形容器放在水平地面上,容器内盛有质量为6千克的液体(ρ液=0.6×103千克/米3)。求:
①容器对水平地面的压力与压强。
②当在液体中浸没一个体积为2×10-4米3的小球时,液体对容器底部压强变化量的范围。
8、金属实心圆柱体甲的密度为2.0×103千克/米3,体积为103米3;底面积为2×102米2的薄壁圆柱形容器乙放在水平地面上,容器内盛有水,水深0.2米。
① 求甲的质量m甲。
② 求水对乙容器底部的压强p水。
③ 若将甲浸没在乙容器的水中,求容器对水平地面压强变化量△p容器的范围。
9、如图1所示,相同的圆柱形容器A和B放在水平地面上,容器的质量为1千克,两容器各盛有2千克的水、酒精(ρ酒精=0.8×103千克/米3)。
① 求0.1米深处水的压强p水。
② 求B容器对水平地面的压力F。
③ 现有质量相等的甲、乙两实心物块,若将甲浸没在水中、乙浸没在酒精中后,两液体均未溢出,且两液体各自对容器底部的压强相等,则甲、乙的密度之比ρ甲︰ρ乙=________________。
10、边长为0.1米和0.3米的甲、乙两正方体放在水平地面上,它们对水平地面的压强相等,已知甲的密度为2×103千克/米3。求:
① 甲质量m甲。
② 乙对地面的压力F乙。
③ 若在正方体甲、乙上沿水平方向分别切去厚度,h甲′和h乙′后,使甲、乙剩余部分对水平地面的压强依然相等,则h甲′︰h乙′=___________(只要求写出结果)
公式法
根据题目中给定条件,列出变化后的压强:
P’=F’/S=(F+ΔF)/S或(F—ΔF)/S;P’=ρgh’=ρg(h+Δh)或ρg(h—Δh);
再进行整体或拆分比较
三态法
① 初始状态。如:相同的容器盛有同种或不同种液体;底面积不同的容器盛有同种或不同种液体;液体的质量、体积、密度、压强、压力等这些物理量。
② 变化过程:倒入液体、抽出液体、放入小球、取出小球。
③ 末状态:分析比较液体产生的压力、压强等。
具体解法如下:
① 根据初始状态判断出液体密度、压强(或压力)的大小。可根据P=F/S P=ρgh ρ=m/V判断。
② 根据末状态找出未知物理量,从而确定变化量(ΔP、ΔF、Δm或ΔV等)。
③ 结合题目所给选项找出改变(增大或减小)ΔP、ΔF、Δm或ΔV等的方法。
变化的压强可以用ΔP=ρgΔh ΔP=ΔF/S等分析;变化的压力可以用ΔF=Δmg ΔF=ΔPS等分析。
三、整体乘积
个别题型中出现计算推导得出的ρgSΔh这样的式子,由上述方法无法解出答案的情况,可以把ρS的乘积看成整体,有题目中给出的条件如原来的压力F大小,化简得出ρS的乘积的大小,再带入计算式中进行比较。
四、乘积拆分
对于上述第三个方法还无法解出答案的题目,可以尝试对上式ρgSΔh中的S再进行拆分,一般拆成ρgh2Δh的形式,这样就可以把ρgh2Δh继续化简成PhΔh的形式,这样就可以进行比较。这种方法一般运用于切割等厚度或剩余等厚度的情况。
除了上述方法外,还有一些其他的特殊方法,如极限法、特值法、比例法等等,具体选择哪种方法要看题目情况而定。
宝山:21.如图9所示,高为1米、底面积为0.5米2的轻质薄壁圆柱形容器置于水平地面上,且容器内盛满水。
⑴求水对容器底部的压强p。
⑵若将一个体积为0.05米3的实心小球慢慢地放入该容器中,当小球静止不动时,发现容器对水平地面的压强没有发生变化。求小球质量的最大值m球最大。
奉贤:21.如图11所示,两个均匀的实心正方体甲和乙放置在水平地面上,甲的质量为6千克,边长为0.1米。求:(1)甲的密度
(2)甲对地面的压强P甲
(3)a.若甲乙对水平地面的压强相等,且密度之比为3:2,现分别在两物体上沿竖直方向切去质量相等的部分并分别放在对方剩余部分上,则甲乙切去部分和地面的接触面积之比
ΔS甲:ΔS乙=
b.若叠放后甲乙对地面的压强的增加量分别为ΔP甲、ΔP乙,且当ΔP甲:ΔP乙=5:1时,甲物体沿竖直方向切去的质量是 千克。(第三小题无需写出计算过程)
虹口:22. 如图10所示,轻质薄壁圆柱形容器置于水平地面,容器盛有质量为4千克的水.
①求水的体积V水;
②求0.1米深处水的压强P水;
③现有质量为4千克的物体,其底面积是容器的一半。若通过两种方法增大地面受到的压强,并测出压强的变化量,如下表所示.
根据表中的信息,通过计算判断将物体放入容器时是否有水溢出,若有水溢出请求出溢出水的重力G溢水,若无水溢出请说明理由.
金山:23.如图14所示,底面积为10?2米2、高为0.4米长方体甲(ρ甲=2×103千克/米3)和底面积为2?10?2米2的薄壁柱形容器乙放在水平地面上。乙容器足够高,内盛有0.1米深的水。
(1)求甲的质量m甲。
(2)求水对乙容器底部的压强p水。
(3)现沿水平方向将长方体甲截取一定的厚度,并将截取部分竖直放入乙容器中,使得水对容器底部的压强最大,且长方体甲对地面的压强减少量最小,请求出甲对地面的压强减少量。
静安:22.盛有水的薄壁圆柱形容器置于水平地面,其底面积为2×10-2米2,甲和乙是由同种金属制成、体积不同的圆柱体。若只在圆柱形容器内轻放入甲(或乙)时,甲(或乙)浸没在水中,且有水溢出容器。现测得甲(或乙)轻放入容器后,容器对桌面的压强p、水对容器底部的压强p'以及溢出水的质量m,并记录在下表中。
① 求容器的高度h。
所放的 圆柱体 容器对桌面的压强p(帕) 水对容器底部的压强p'(帕) 溢出水的质量m(千克)
甲 9800 4900 2
乙 11760 4900 4
② 求放入甲后容器对桌面的压力F甲。
③(a)求甲、乙质量的差值?m;
(b)求制成圆柱体金属的密度?。
闵行:24. 如图16所示,某薄壁柱形容器中装有质量为2千克的水,放在水平地面上,容器的质量为1千克,底面积为0.01米2。求:
(1)容器内水的体积;
(2)容器对桌面的压强;
(3)若把一个实心均匀的小球放入水中,小球浸没并且沉底,水没有溢出。如果水对容器底部压强与容器对地面压强的比值在放入小球前后保持不变,求小球的密度.
浦东新区:22.如图10所示,甲、乙两个质量均为2千克的实心均匀圆柱体放在水平地面上。甲的底面积为4×10-3米2,乙的体积为0.8×10-3米3。求:
①乙的密度ρ乙;
②甲对地面的压强p甲;
③若甲的底面积是乙的1.5倍,在甲、乙的上部沿水平方向分别切去Δm甲和Δm乙,再将切去部分互叠在对方剩余部分的上方,使甲、乙对水平地面的压强相等。请比较Δm甲和Δm乙的大小关系及求出两者的差值。
普陀:21.如图8所示,水平放置的轻质圆柱形容器底面积为2×10-2米2,内装有重为9.8N的水,现将体积为2×10-4米3、重为4.9N实心金属球A用细线栓着浸没在水中。
①求金属块A受到的浮力F浮
②求水对容器底部的压力F水
③现将绳子剪断,求绳子剪断后容器对水平地面压强变化了ΔP
青浦:25.柱形轻质薄壁容器的底面积为1×102米2,如图11所示,内盛0.2米深度的水后置于水平地面上。
① 求容器底部受到水的压强p水。
② 现将一块质量为1.5千克、体积为1×10?3米3的物体完全浸没在容器的水中后,测得容器底部受到水的压强为2450帕。求此时容器对水平桌面的压强p容。
松江:21.如图15所示,柱形容器A和均匀实心圆柱体B置于水平地面上,A中盛有体积为6×10-3米3的水,B受到的重力为250牛,B的底面积为5×10-2米2。求:
① A中水的质量m水。
② B对水平地面的压强pB。
③ 现沿水平方向在圆柱体B上截去一定的厚度,B剩余部分的高度与容器A中水的深度之比hB∶h水为2∶3,且B剩余部分对水平地面的压强等于水对容器A底部的压强,求:B的密度ρB。
徐汇:24. 如图14(a)所示,两个完全相同的薄壁圆柱形容器放在水平地面上。容器中分别盛有酒精和水,酒精的体积为3×10-3米3(已知ρ酒精=0.8×103千克/米3)。将图14(b)所示的实心圆柱形金属块(底面积为容器底面积的一半),分别竖直放入酒精和水中(液体
都不溢出),同时测出放入金属块前后酒精和水对容器底部的压强P酒和P水,如下表所示。求:
①酒精的质量m酒
②放入金属块前容器中水的深度h水。
③已知金属块放入液体后有浸没、未浸没、恰好浸没三种状态。
i ) 分析比较金属块放入酒精前后,酒精的压强:P酒′<2 P酒,可推出h酒′<2 h酒;同时结合已知条件S金=S容/2,可分析推出:金属块在酒精中处于____________状态。
ii) 分析比较金属块放水中入前后,水的压强:______________,可知_______________可分析推出:金属块在水中处于未浸没或恰好浸没状态。
iii) 进一步综合分析,并通过计算说明金属块在水中所处的状态。
杨浦:25. 如图16所示,水平地面上置有轻质薄壁圆柱形容器甲和圆柱体乙。甲的底面积为0.01米、高为0.3米,盛有0.2米深的水;乙的底面积为0.005米、高为0.8米,质量为8千克.
①求水对甲底部的压强;
②求乙的密度;
③若在乙上方沿水平方向切去一部分,并将切去部分竖直放在甲容器内,此时水对容器底部的压力等于乙剩余部分对地面的压力,求甲容器对地面压强的变化量.
长宁:25.如图9所示,底面积分别为0.02米2和0.01米2的柱形容器甲和乙置于水平桌面上,容器受到的重力均为10.8牛,容器甲中水的深度为0.2米,容器乙中酒精的深度为0.3米。(ρ酒精=0.8×103千克/米3)
求:①酒精对容器乙底部的压强p酒。
②容器甲对水平桌面的压强p甲。
③为了使容器甲和乙中的液体对各自容器底部的压强相等,小明设计的方案是:只向容器甲中倒入体积为ΔV1的水;小华设计的方案是:只从容器乙中抽出体积为ΔV2的酒精。
请计算或ΔV2其中任意一个的大小。
同课章节目录
- 第一章 打开物理世界的大门
- 第一节 走进神奇
- 第二节 探索之路
- 第三节 站在巨人的肩膀上
- 第二章 运动的世界
- 第一节 动与静
- 第二节 长度与时间的测量
- 第三节 快与慢
- 第四节 科学探究:速度的变化
- 第三章 声的世界
- 第一节 科学探究:声音的产生与传播
- 第二节 声音的特性
- 第三节 超声与次声
- 第四章 多彩的光
- 第一节 光的反射
- 第二节 平面镜成像
- 第三节 光的折射
- 第四节 光的色散
- 第五节 科学探究:凸透镜成像
- 第六节 神奇的眼睛
- 第五章 质量与密度
- 第一节 质量
- 第二节 学习使用天平和量筒
- 第三节 科学探究:物质的密度
- 第四节 密度知识的应用
- 第六章 熟悉而陌生的力
- 第一节 力
- 第二节 怎样描述力
- 第三节 弹力与弹簧测力计
- 第四节 来自地球的力
- 第五节 科学探究:摩擦力
- 第七章 力与运动
- 第一节 科学探究:牛顿第一定律
- 第二节 力的合成
- 第三节 力的平衡
- 第八章 压强
- 第一节 压力的作用效果
- 第二节 科学探究:液体的压强
- 第三节 空气的“力量”
- 第四节 流体压强与流速的关系
- 第九章 浮力
- 第一节 认识浮力
- 第二节 阿基米德原理
- 第三节 物体的浮与沉
- 第十章 机械与人
- 第一节 科学探究:杠杆的平衡条件
- 第二节 滑轮及其应用
- 第三节 做功了吗
- 第四节 做功的快慢
- 第五节 机械效率
- 第六节 合理利用机械能
- 第十一章 小粒子与大宇宙
- 第一节 走进微观
- 第二节 看不见的运动
- 第三节 探索宇宙
