人教版数学七年级下册9.1.1不等式及其解集 (1)(共16张PPT)
文档属性
| 名称 | 人教版数学七年级下册9.1.1不等式及其解集 (1)(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 469.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-17 00:00:00 | ||
图片预览




文档简介
9.1 不等式
不等式及其解集
你还记得小孩玩的翘翘板吗?你想过它的工作原
理吗?其实,翘翘板就是靠不断改变两端的重量
对比来工作的.
看一看
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
由此可见,“不相等”处处可见。
从今天起,我们开始学习一类新的数学知识:
不等式.
不相等 处处可见
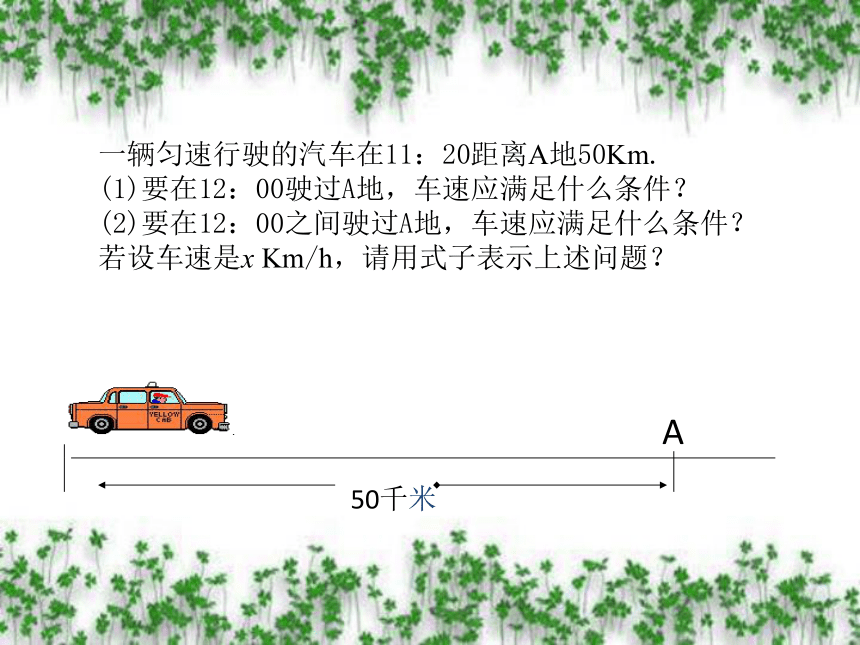
A
50千米
一辆匀速行驶的汽车在11:20距离A地50Km.
(1)要在12:00驶过A地,车速应满足什么条件?
(2)要在12:00之间驶过A地,车速应满足什么条件?
若设车速是x Km/h,请用式子表示上述问题?
(1)汽车在12:00之前驶过A地的意思是什么?
从时间上看,汽车要在12:00之前驶过A地,则
以这个速度行驶50 km所用的时间不到 .
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶 的路程要超过50 km.
问题1 一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地.你能用式子表示出车速应满足的条件吗?
合作探究 达成目标
探究点一 不等式的概念
(2)如何用式子表示以上不等关系?
设:车速为x km/h.
从时间上看:
从路程上看:
问题1 一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地.你能用式子表示出车速应满足的条件吗?
“ < ”
“ > ”
“ ≠ ”
“ ≤ ”
“ ≥ ”
小于
大于
不等于
不大于(小于或等于)
不小于(大于或等于)
“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号
定义:用“>”或“<”号表示大小关系的式子,叫做不等式,像a+2≠a这样用“ ≠”号表示不等关系的式子也是不等式。
(1)对于不等式 而言,车速可以是80 km/h吗?78 km/h呢?75 km/h呢?72 km/h呢?
当x=80时, ;
当x=78时, ;
当x=75时, ;
当x=80时, .
问题2 一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地.你能求出车速应的取值吗?
类比方程的解,什么叫不等式的解?
使不等式成立的未知数的值.
(3)不等式 还有其他解吗?如果有,
这些解应满足什么条件?
满足
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.求不等式的解集的过程叫做解不等式.
(4)除了用不等式 表示取值范围,
还有其他表示方法吗?
不等式的解是指在不等式解集的范围内某一个具体的数值,而不等式的解集是不等式所有的解的集合.在数轴上表示不等式的解集时,应注意画空心圆圈表示不包括这一点,画实心圆圈表示包括这一点.
不等式的解与解集有什么区别?
怎样在数轴上表示不等式的解集?
上交作业:教科书习题9.1第1,2题.;
达标检测 反思目标
不等式及其解集
你还记得小孩玩的翘翘板吗?你想过它的工作原
理吗?其实,翘翘板就是靠不断改变两端的重量
对比来工作的.
看一看
在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,
并把它们用到了生活实践当中.
由此可见,“不相等”处处可见。
从今天起,我们开始学习一类新的数学知识:
不等式.
不相等 处处可见
A
50千米
一辆匀速行驶的汽车在11:20距离A地50Km.
(1)要在12:00驶过A地,车速应满足什么条件?
(2)要在12:00之间驶过A地,车速应满足什么条件?
若设车速是x Km/h,请用式子表示上述问题?
(1)汽车在12:00之前驶过A地的意思是什么?
从时间上看,汽车要在12:00之前驶过A地,则
以这个速度行驶50 km所用的时间不到 .
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶 的路程要超过50 km.
问题1 一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地.你能用式子表示出车速应满足的条件吗?
合作探究 达成目标
探究点一 不等式的概念
(2)如何用式子表示以上不等关系?
设:车速为x km/h.
从时间上看:
从路程上看:
问题1 一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地.你能用式子表示出车速应满足的条件吗?
“ < ”
“ > ”
“ ≠ ”
“ ≤ ”
“ ≥ ”
小于
大于
不等于
不大于(小于或等于)
不小于(大于或等于)
“<” 、“>” 、“≠”、“ ≤”、“ ≥”都是不等号
定义:用“>”或“<”号表示大小关系的式子,叫做不等式,像a+2≠a这样用“ ≠”号表示不等关系的式子也是不等式。
(1)对于不等式 而言,车速可以是80 km/h吗?78 km/h呢?75 km/h呢?72 km/h呢?
当x=80时, ;
当x=78时, ;
当x=75时, ;
当x=80时, .
问题2 一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地.你能求出车速应的取值吗?
类比方程的解,什么叫不等式的解?
使不等式成立的未知数的值.
(3)不等式 还有其他解吗?如果有,
这些解应满足什么条件?
满足
一般地,一个含有未知数的不等式的所有的解,组成这个不等式的解集.求不等式的解集的过程叫做解不等式.
(4)除了用不等式 表示取值范围,
还有其他表示方法吗?
不等式的解是指在不等式解集的范围内某一个具体的数值,而不等式的解集是不等式所有的解的集合.在数轴上表示不等式的解集时,应注意画空心圆圈表示不包括这一点,画实心圆圈表示包括这一点.
不等式的解与解集有什么区别?
怎样在数轴上表示不等式的解集?
上交作业:教科书习题9.1第1,2题.;
达标检测 反思目标
