27.4 正多边形和圆 教案(表格式)
文档属性
| 名称 | 27.4 正多边形和圆 教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 960.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-17 00:00:00 | ||
图片预览


文档简介
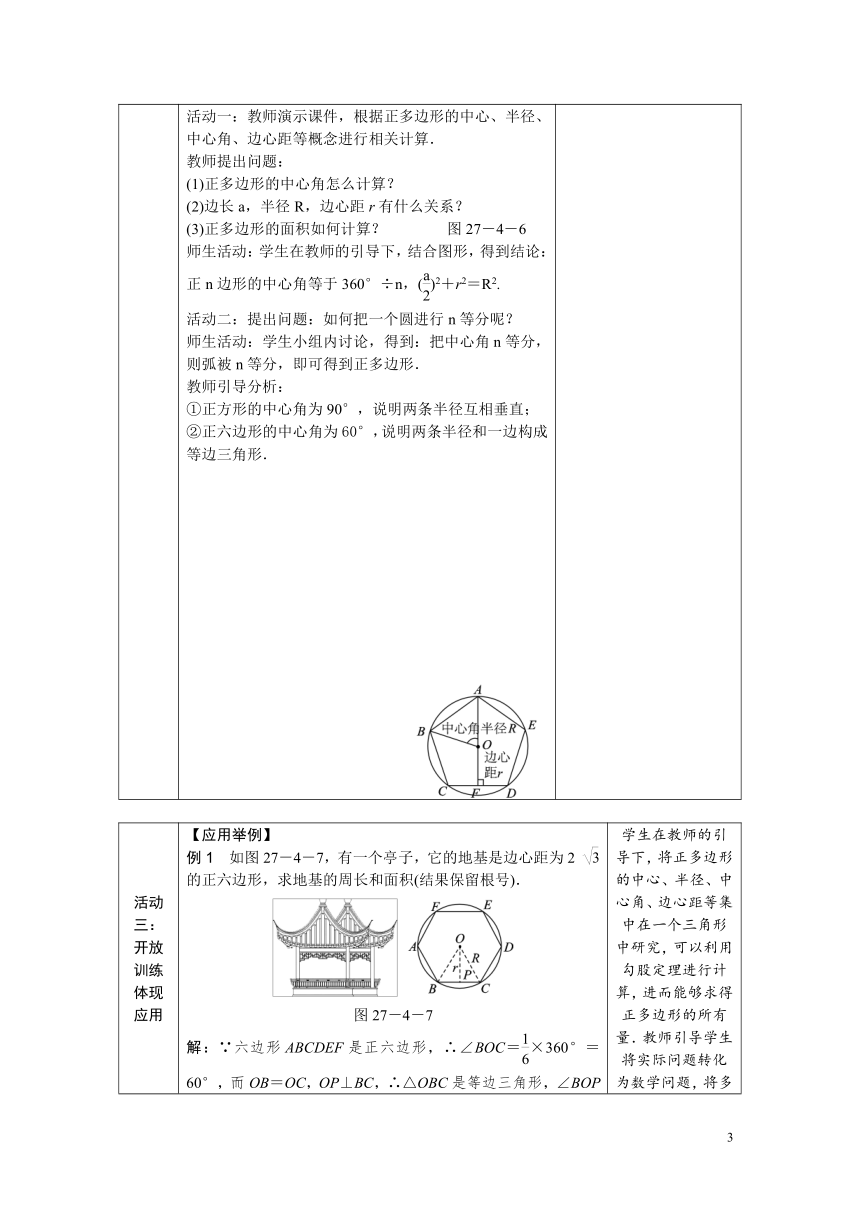
课题 27.4 正多边形和圆 授课人
教学目标 知识技能 使学生经历正多边形的形成过程,了解正多边形的有关概念,掌握用等分圆周画圆的内接正多边形的方法;能应用正多边形的边角关系进行有关计算.
数学思考 使学生丰富对正多边形的认识,通过设计图案,发展学生的形象思维.
问题解决 使学生会等分圆周,利用等分圆周的方法构造正多边形,并会设计图案,发展学生的实践能力和创新精神.
情感态度 通过等分圆周、构造正多边形等实践活动,使学生在数学学习活动中获得成功的体验,建立自信心.
教学重点 理解掌握正多边形的半径、中心角、边心距、边等名称及其求法.
教学难点 探索正多边形和圆的关系.
授课类型 新授课 课时
教具 多媒体
教学活动
教学步骤 师生活动 设计意图
回顾 (多媒体演示)问题: 1.切线长定理的内容是什么?请画出一个三角形的内切圆. 2.请画出垂径定理的基本图形,并说明其中的数量关系. 3.什么是正多边形?你对正多边形有多少了解?师生活动:教师引导学生进行解答,并适时做出补充和讲解. 回顾以前学习过的且对本节课的学习有基础作用的知识,为学习新知打下基础.
活动一:创设情境导入新课 【课堂引入】(课件展示)观看下列美丽的图案,提出问题: 图27-4-4 (1)你能从这些美丽的图案中找出正多边形吗?(2)你知道正多边形和圆有什么关系吗?怎样作出一个正多边形呢?师生活动:教师引导学生观察、思考,学生讨论、交流,发表各自见解.教师关注:①学生能否从图案中找出正多边形;②学生能否从图案中发现正多边形和圆的关系. 创设情境,使学生主动将圆的知识与正多边形联系起来,激发学生探索的热情,调动学生学习的积极性.
活动二:实践探究交流新知 【探究新知】问题1:将一个圆分为五等份,依次连结各分点得到一个五边形,这个五边形一定是正多边形吗?如果是,请你证明这个结论.师生活动:教师演示作图并提示学生从正多边形的定义入手证明,引导学生观察、分析,教师指导学生完成证明过程.教师在学生思考、交流的基础上板书证明过程: 图27-4-5 如图27-4-5,∵====,∴AB=BC=CD=DE=EA.∵==3,∴∠C=∠D.同理可证:∠A=∠B=∠C=∠D=∠E,∴五边形ABCDE是正五边形.∵A,B,C,D,E在⊙O上,∴五边形ABCDE是圆内接正五边形.
活动二:实践探究交流新知 教师小结:圆心O到各边的距离都相等,记为r,那么以点O为圆心、r为半径的圆就与正五边形的各条边都相切,它就是正五边形的内切圆.归纳:任何一个正多边形都有一个外接圆和一个内切圆.这两个圆有公共的圆心,称其为正多边形的中心.外接圆的半径叫做正多边形的半径,内切圆的半径叫做正多边形的边心距.正多边形每一条边所对的外接圆的圆心角都相等,叫做正多边形的中心角.问题2:如果将圆n等分,依次连结各分点得到一个n边形,这个n边形一定是正n边形.师生活动:学生思考,然后小组内交流、讨论,教师根据学生的回答进行总结.教师重点关注:学生能否按照证明圆内接正五边形的方法证明圆内接正n边形.问题3:各边相等的圆内接多边形是正多边形吗?各角相等的圆内接多边形呢?请说明理由.师生活动:学生讨论,思考回答,教师进行总结讲解.教师重点关注:学生能否利用正多边形的定义进行判断;学生能否由圆内接正多边形的各边相等得到弦相等及弦所对的弧相等;学生能否举反例说明各角相等的圆内接多边形不一定是正多边形.【应用新知】活动一:教师演示课件,根据正多边形的中心、半径、中心角、边心距等概念进行相关计算.教师提出问题:(1)正多边形的中心角怎么计算?(2)边长a,半径R,边心距r有什么关系?(3)正多边形的面积如何计算? 图27-4-6师生活动:学生在教师的引导下,结合图形,得到结论:正n边形的中心角等于360°÷n,()2+r2=R2.活动二:提出问题:如何把一个圆进行n等分呢?师生活动:学生小组内讨论,得到:把中心角n等分,则弧被n等分,即可得到正多边形.教师引导分析:①正方形的中心角为90°,说明两条半径互相垂直;②正六边形的中心角为60°,说明两条半径和一边构成等边三角形. 1.将结论由特殊推广到一般,符合学生的认知规律,并交给学生一种研究问题的方法.2.教学中,使学生明确圆内接正多边形必须满足各边相等,各角相等,培养学生严谨的态度和思维批判性.3.通过学生探索、归纳,教给学生等分圆周的方法,尤其是尺规作正方形、正六边形.
活动三:开放训练体现应用 【应用举例】例1 如图27-4-7,有一个亭子,它的地基是边心距为2 的正六边形,求地基的周长和面积(结果保留根号). 图27-4-7解:∵六边形ABCDEF是正六边形,∴∠BOC=×360°=60°,而OB=OC,OP⊥BC,∴△OBC是等边三角形,∠BOP=∠COP=30°,∴BC=OB,cos30°=,而OP=2 ,∴BC=OB=4,∴该地基的周长=4×6=24,面积=6××4×2 =24 .师生活动:教师引导学生画出图形,进行分析,完成例题的解答.教师总结:正六边形中由两条半径和边组成的三角形为等边三角形,所以半径与边相等,所以正六边形的周长为半径的6倍;正六边形的面积分割为六个全等的等边三角形,先求每个等边三角形的面积再乘6即可.变式训练如图27-4-8,正六边形螺帽的边长是2 cm,这个扳手的开口a的值应是(A)A.2 cm B. cm 图27-4-8C. cm D.1 cm 学生在教师的引导下,将正多边形的中心、半径、中心角、边心距等集中在一个三角形中研究,可以利用勾股定理进行计算,进而能够求得正多边形的所有量.教师引导学生将实际问题转化为数学问题,将多边形问题转化为三角形问题.
【拓展提升】例2 已知半径为R的⊙O,用多种工具、多种方法作出圆内接正三角形.师生活动:学生先独立解决问题,然后小组中讨论,鼓励学生勇于探索实践,然后与同桌交流,上讲台演示,教师要重点关注学生的解题过程.图27-4-9
(续表)
活动三:开放训练体现应用 方法一:①用量角器画圆心角∠AOB=120°,∠BOC=120°;②连结AB,BC,CA,则△ABC为圆内接正三角形.方法二:①用量角器画圆心角∠BOC=120°;②在⊙O上用圆规截取弧AB=弧BC;③连结AC,BC,AB,则△ABC为圆内接正三角形.方法三:①作直径AD;②以点D为圆心,OD长为半径画弧,交⊙O于点B,C;③连结AB,BC,CA,则△ABC为圆内接正三角形.例3 如图27-4-10,AB,CD是⊙O中互相垂直的两条直径,以点A为圆心,OA为半径画弧,与⊙O交于E、F两点.(1)求证:AE是正六边形的一边;(2)请在图上继续画出这个正六边形.解:(1)证明:连结OE,OF,AF,∵AE=OA=OE,∴△AOE是等边三角形,故∠OAE=60°,同理可证:△OAF是等边三角形.∴∠OAF=60°,∴AE=AF,且∠EAF=∠OAE+∠OAF=120°,∴AE是正六边形的一边. 图27-4-10(2)以B为圆心,AE长为半径画弧,与⊙O交于点G,H,然后顺次将A,E,G,B,H和F连结起来就得到正六边形. 及时获知学生对所学知识的掌握情况,落实本课的学习目标.分层设计可让不同程度的同学最大限度地发挥他们的潜力,树立学好数学的信心.
活动四:课堂总结反思 【达标测评】 1.若正六边形的边长为6,则其外接圆半径与内切圆半径的大小分别为(B)A.6,3 B.6,3 C.3 ,6 D.6,3 2.如图27-4-11,在⊙O中,OA=AB,OC⊥AB,交⊙O于点C,那么下列结论错误的是(A)A.∠BAC=30° B.=C.线段OB的长等于圆内接正六边形的半径D.弦AC的长等于圆内接正十二边形的边长 图27-4-11 图27-4-12 3.如图27-4-12,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=位于第一象限的图象上,则k的值为__9___.
(续表)
活动四:课堂总结反思 4.如图27-4-13,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.(1)写出图中所有的等腰三角形; (2)求证:∠G=2∠F. 图27-4-13解:(1)∵五边形ABCD是正五边形,∴AB=BC=CD=DE=EA,∠ABC=∠BCD=∠CDE=∠DEA=∠EAB=108°,∵DC=BC,∴△CDB是等腰三角形.∵∠C=108°,∴∠1=∠CBD=36°.∵AF∥CD,∴∠F=∠1=36°.∵∠ABD=∠ABC-∠CBD=108°-36°=72°,∴∠F=∠BAF=36°,∴△BAF是等腰三角形,进而可得∠GEA=∠G=∠2=72°,∴△FDG,△AEG是等腰三角形,故等腰三角形有△BCD,△ABF,△FDG,△AEG.(2)证明:∵五边形ABCDE是正五边形,∴∠C=∠CDE=108°,CD=CB,得∠1=36°,∴∠2=108°-36°=72°.又∵AF∥CD,∴∠F=∠1=36°,故∠G=180°-∠2-∠F=180°-72°-36°=72°=2∠F.师生活动:学生完成达标测评后,教师进行个别提问,并指导学生解释做题理由和做题方法,使学生在个别思考解答的基础上,共同交流、形成共识、确定答案. 设置达标测评的目的是使学生加深对所学知识的理解和运用,在问题的选择上以基础为主、疑难点突出,增加开放型、探究型问题,使学生思维得到拓展、能力得以提升.
【课堂小结】(1)谈一谈你在本节课中有哪些收获?哪些进步?(2)学习本节课后,还存在哪些困惑?布置作业:教材P67习题27.4第1,2,3题. 巩固、梳理所学知识.对学生进行鼓励、进行思想教育.
【知识网络】 提纲挈领,重点突出.
(续表)
活动四: 课堂 总结 反思 【教学反思】①[授课流程反思]在探究新知的过程中,使学生认识到事物之间是普遍联系的,是可以相互转化的,并培养和训练学生综合运用知识和解决实际问题的意识,渗透数形结合的思想和方法.②[讲授效果反思]引导学生注意以下几点:(1)正多边形的相关概念;(2)正多边形中的相关计算;(3)正多边形的画法.③[师生互动反思]从学生课堂发言和表现来看,学生能够主动参与,亲身体验知识的发生和发展过程,学有所获.④[习题反思]好题题号__________________________________________错题题号__________________________________________ 反思教学过程和教师表现,进一步提升操作流程和自身素质.
PAGE
1
