27.2.2 直线与圆的位置关系导学案(无答案)
文档属性
| 名称 | 27.2.2 直线与圆的位置关系导学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 513.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-17 00:00:00 | ||
图片预览

文档简介
27.2.2 直线与圆的位置关系
【学习目标】
1、使学生掌握直线与圆的位置关系,能用数量来判断直线与圆的位置关系。
2、进一步体会分类讨论思想。
【学习重点】
用数量关系(圆心到直线的距离)判断直线与圆的位置关系。
【学习难点】
用数量关系(圆心到直线的距离)判断直线与圆的位置关系。
【课标要求】
了解切线的概念,探索切线与过切点的半径之间的关系,掌握切线的识别方法。
【知识回顾】
情境导入:用移动的观点认识直线与圆的位置关系
1、同学们也许看过海上日出,如右图中,如果我们把太阳看作一个圆,那么太阳在升起的过程中,它和海平面就有右图中的三种位置关系。
2、请同学在纸上画一条直线,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线与圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
【自主学习】
从以上的两个例子,可以看到,直线与圆的位置关系只有以下三种,
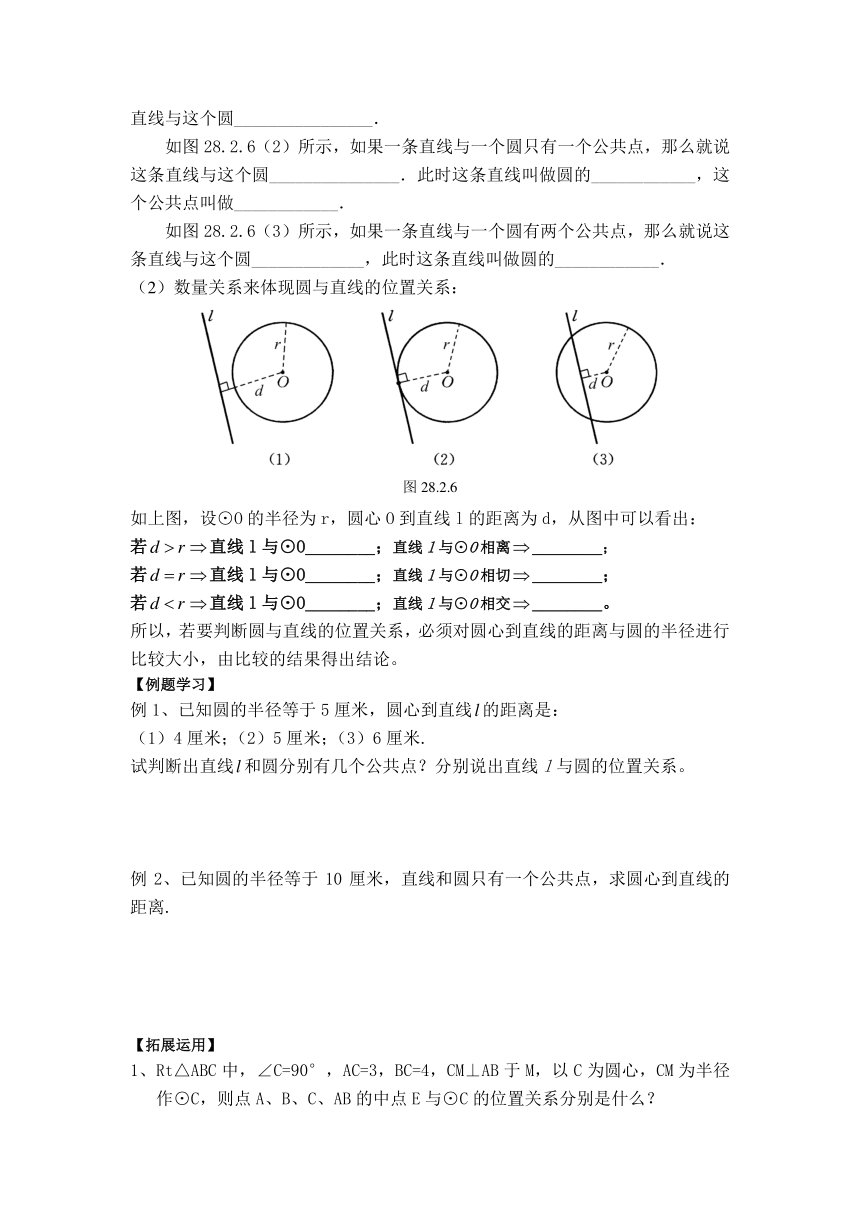
(1)直线与圆的位置关系的概念:如下图所示:
如图28.2.6(1)所示,如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆________________.
如图28.2.6(2)所示,如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆_______________.此时这条直线叫做圆的____________,这个公共点叫做____________.
如图28.2.6(3)所示,如果一条直线与一个圆有两个公共点,那么就说这条直线与这个圆_____________,此时这条直线叫做圆的____________.
(2)数量关系来体现圆与直线的位置关系:
如上图,设⊙O的半径为r,圆心O到直线l的距离为d,从图中可以看出:
若直线l与⊙O________;直线l与⊙O相离________;
若直线l与⊙O________;直线l与⊙O相切________;
若直线l与⊙O________;直线l与⊙O相交________。
所以,若要判断圆与直线的位置关系,必须对圆心到直线的距离与圆的半径进行比较大小,由比较的结果得出结论。
【例题学习】
例1、已知圆的半径等于5厘米,圆心到直线的距离是:
(1)4厘米;(2)5厘米;(3)6厘米.
试判断出直线和圆分别有几个公共点?分别说出直线l与圆的位置关系。
例2、已知圆的半径等于10厘米,直线和圆只有一个公共点,求圆心到直线的距离.
【拓展运用】
Rt△ABC中,∠C=90°,AC=3,BC=4,CM⊥AB于M,以C为圆心,CM为半径作⊙C,则点A、B、C、AB的中点E与⊙C的位置关系分别是什么?
【归纳小结】
本节课我们学习了直线与圆的位置关系,当我们判断直线与圆的位置关系时,应该用数量关系(圆心到直线的距离)来体现,即上面讲解的圆心到直线的距离与圆的半径进行比较大小,从而断定是哪种关系。
【堂清】
如果⊙O的直径为10厘米,圆心O到直线AB的距离为10厘米,那么⊙O与直线AB有怎样的位置关系?
【作业】
1、直线与⊙O相切,若圆心O到直线的距离是5,则⊙O的半径是______.
2、已知⊙O的半径为3cm,圆心O到直线的距离是4cm,则直线与⊙O的位置关是________________.
3、已知⊙O的半径为6,点O到直线的距离为5,则直线与⊙O的位置关系是( )
A. 相切 B.相离 C.相交 D.不确定
4、如图,在Rt△ABC中,∠C = 90°,∠B = 30°,BC = 4 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是( ).
A.相离 B.相切 C.相交 D.相切或相交
5、已知⊙O的直径为10cm,圆心O到直线的距离分别为3cm,5cm,7cm时,则直线与⊙O的位置关系分别是( ).
A.相交、相离、相切 B.相离、相交、相切
C.相切、相交、相离 D.相交、相切、相离
6、如图,在矩形ABCD中,AB=6,BC=4,⊙O是以AB为直径的圆,则直线DC与⊙O的位置关系是_____________.
7、在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定( )。
A.与x轴相离,与y轴相切 B.与x轴,y轴都相离
C.与x轴相切,与y轴相离 D.与x轴,y轴都相切
8、若以点P(3,)为圆心的圆与x轴相切,则这个圆与y轴的位置关系一定是( )
A.相离 B.相切 C.相交 D.不确定
9、已知⊙O的半径为r,点O到直线的距离为d,且。试判断⊙O与直线的位置关系
【学习目标】
1、使学生掌握直线与圆的位置关系,能用数量来判断直线与圆的位置关系。
2、进一步体会分类讨论思想。
【学习重点】
用数量关系(圆心到直线的距离)判断直线与圆的位置关系。
【学习难点】
用数量关系(圆心到直线的距离)判断直线与圆的位置关系。
【课标要求】
了解切线的概念,探索切线与过切点的半径之间的关系,掌握切线的识别方法。
【知识回顾】
情境导入:用移动的观点认识直线与圆的位置关系
1、同学们也许看过海上日出,如右图中,如果我们把太阳看作一个圆,那么太阳在升起的过程中,它和海平面就有右图中的三种位置关系。
2、请同学在纸上画一条直线,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线与圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
【自主学习】
从以上的两个例子,可以看到,直线与圆的位置关系只有以下三种,
(1)直线与圆的位置关系的概念:如下图所示:
如图28.2.6(1)所示,如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆________________.
如图28.2.6(2)所示,如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆_______________.此时这条直线叫做圆的____________,这个公共点叫做____________.
如图28.2.6(3)所示,如果一条直线与一个圆有两个公共点,那么就说这条直线与这个圆_____________,此时这条直线叫做圆的____________.
(2)数量关系来体现圆与直线的位置关系:
如上图,设⊙O的半径为r,圆心O到直线l的距离为d,从图中可以看出:
若直线l与⊙O________;直线l与⊙O相离________;
若直线l与⊙O________;直线l与⊙O相切________;
若直线l与⊙O________;直线l与⊙O相交________。
所以,若要判断圆与直线的位置关系,必须对圆心到直线的距离与圆的半径进行比较大小,由比较的结果得出结论。
【例题学习】
例1、已知圆的半径等于5厘米,圆心到直线的距离是:
(1)4厘米;(2)5厘米;(3)6厘米.
试判断出直线和圆分别有几个公共点?分别说出直线l与圆的位置关系。
例2、已知圆的半径等于10厘米,直线和圆只有一个公共点,求圆心到直线的距离.
【拓展运用】
Rt△ABC中,∠C=90°,AC=3,BC=4,CM⊥AB于M,以C为圆心,CM为半径作⊙C,则点A、B、C、AB的中点E与⊙C的位置关系分别是什么?
【归纳小结】
本节课我们学习了直线与圆的位置关系,当我们判断直线与圆的位置关系时,应该用数量关系(圆心到直线的距离)来体现,即上面讲解的圆心到直线的距离与圆的半径进行比较大小,从而断定是哪种关系。
【堂清】
如果⊙O的直径为10厘米,圆心O到直线AB的距离为10厘米,那么⊙O与直线AB有怎样的位置关系?
【作业】
1、直线与⊙O相切,若圆心O到直线的距离是5,则⊙O的半径是______.
2、已知⊙O的半径为3cm,圆心O到直线的距离是4cm,则直线与⊙O的位置关是________________.
3、已知⊙O的半径为6,点O到直线的距离为5,则直线与⊙O的位置关系是( )
A. 相切 B.相离 C.相交 D.不确定
4、如图,在Rt△ABC中,∠C = 90°,∠B = 30°,BC = 4 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是( ).
A.相离 B.相切 C.相交 D.相切或相交
5、已知⊙O的直径为10cm,圆心O到直线的距离分别为3cm,5cm,7cm时,则直线与⊙O的位置关系分别是( ).
A.相交、相离、相切 B.相离、相交、相切
C.相切、相交、相离 D.相交、相切、相离
6、如图,在矩形ABCD中,AB=6,BC=4,⊙O是以AB为直径的圆,则直线DC与⊙O的位置关系是_____________.
7、在平面直角坐标系中,以点(2,3)为圆心,2为半径的圆必定( )。
A.与x轴相离,与y轴相切 B.与x轴,y轴都相离
C.与x轴相切,与y轴相离 D.与x轴,y轴都相切
8、若以点P(3,)为圆心的圆与x轴相切,则这个圆与y轴的位置关系一定是( )
A.相离 B.相切 C.相交 D.不确定
9、已知⊙O的半径为r,点O到直线的距离为d,且。试判断⊙O与直线的位置关系
