17.2.2 函数的图象练习(无答案)
文档属性
| 名称 | 17.2.2 函数的图象练习(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 542.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-17 16:24:28 | ||
图片预览


文档简介
17.2.2 函数的图象
1.把下面画函数y=-x+2的图象的过程补充完整.
解:(1)列表为:
x
…
-2
-1
0
1
2
3
…
y=-x+2
…
…
(2)画出的函数图象为:
图5
2.周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图6所示,下列说法中正确的是( )
A.小涛家离报亭的距离是900 m
B.小涛从家去报亭的平均速度是60 m/min
C.小涛从报亭返回家中的平均速度是80 m/min
D.小涛在报亭看报用了15 min
图6
图7
3.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t的函数关系图象如图7所示,则休息后园林队每小时绿化面积为________平方米.
4.2018年五一劳动节期间,小张和朋友驾车自助旅游,如图8中的图象描述了小张驾驶的汽车离出发地的路程s(千米)和行驶所用时间t(时)之间的函数关系,请你根据图象,提供小张和朋友驾车自助旅游中的一些具体信息.(至少提供3条与图中的图象有关的信息)
图8
5.“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打6折,设购买种子数量为x(千克),付款金额为y(元),则y与x的函数关系的图象大致是( )
图9
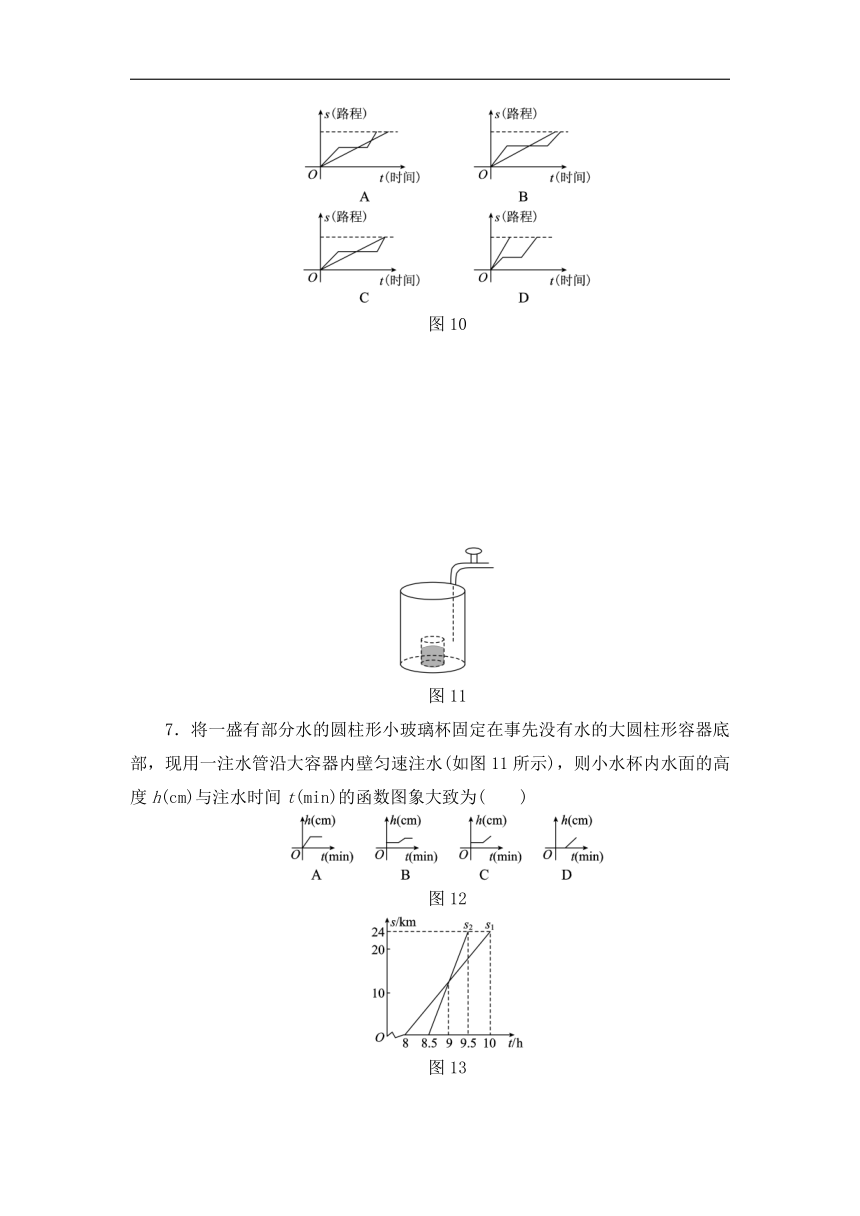
6. “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终赢得比赛,下列函数图象可以体现这一故事过程的是( )
图10
图11
7.将一盛有部分水的圆柱形小玻璃杯固定在事先没有水的大圆柱形容器底部,现用一注水管沿大容器内壁匀速注水(如图11所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
图12
图13
8.小亮家与姥姥家相距24 km,小亮8:00从家出发,骑自行车去姥姥家,妈妈8:30从家出发,乘车沿相同路线去姥姥家,小亮和妈妈的行进路程s(km)与时间t(h)的函数图象如图13所示,则下列说法中错误的有( )
①小亮骑自行车的平均速度是12 km/h;
②妈妈比小亮提前0.5 h到达姥姥家;
③妈妈在距家12 km处追上小亮;
④9:30妈妈追上小亮.
A.1个 B.2个
C.3个 D.4个
9.图14是小明从学校回到家里行进的路程s(米)与时间t(分)的函数图象.观察图象,从中得到如下信息:①学校离小明家1000米;②小明用了20分钟到家;③小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走得快.其中正确的有__________.(填序号)
图14
图15
10.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图15所示,当乙到达终点A时,甲还需________分钟到达终点B.
11.有一个水箱,它的容积是500 L,水箱内原有水200 L,现需将水箱注满,已知每分钟注水10 L.
(1)写出水箱内水量Q(L)与时间t(min)的函数关系式;
(2)求出自变量的取值范围;
(3)画出Q关于t的函数关系图象.
12.如图16所示,A,B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程s(千米)与该日下午时间t(时)之间的关系.
根据图象回答下列问题:
(1)甲和乙哪一个出发得更早?早出发多长时间?
(2)甲和乙哪一个更早到达B地,早多长时间?
(3)描述一下甲的运动情况;
(4)请你根据图象上的数据,分别求出乙骑摩托车的速度和甲骑自行车在全程的平均速度.
图16
13.汽车在行驶过程中,速度往往是变化的,下图图象表示的是一辆汽车的速度随时间变化而变化的情况.
汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
汽车在哪些时间段保持匀速行驶?时速分别是多少?
出发后8分钟到10分钟之间可能发生了什么情况?
14.甲、乙两人(甲骑自行车,乙骑摩托车)从A城出发到B地旅行,如图表示甲、乙两人离开A城的路程与时间之间的函数图象.根据图象,你能得到关于甲、乙两人旅行的哪些信息?
答题要求:(1)请至少提供四条信息,如,由图象可知:甲比乙早出发4小时;甲离开A城的路程与时间的函数图象是一条折线段,说明甲作变速运动.
(2)不要再提供“(1)”中已列举的信息:① ;② ;③ ;④ .
15.甲、乙、丙三人同时从A村出发去B村,刚开始甲骑自行车载乙,丙步行;a小时后甲骑车中途回头接丙,乙步行,结果三人同时到达B地.假设:乙、丙步行速度相同,甲载乙与甲载丙时速度相同,甲载人与不载人时的速度不同,甲、乙、丙三人与A村之间的距离y(千米)与出发的时间x(小时)之间的函数关系如图.(掉头与上下车时间忽略不计)
(1)选择:
甲与A村之间的距离y(千米)与出发时间x(小时)之间的函数图象为折线( )
A、O-M-P??? ?B、O-N-P?? ? C、O-M-N-P???? D、O-N-M-P
乙与A村之间的距离y(千米)与出发时间x(小时)之间的函数图象为折线( )
A、O-M-P???? B、O-N-P???? C、O-M-N-P???? D、O-N-M-P
丙与A村之间的距离y(千米)与出发时间x(小时)之间的函数图象为折线( )
A、O-M-P???? B、O-N-P???? C、O-M-N-P???? D、O-N-M-P
(2)求步行速度,和甲载人骑车时的速度;
(3)求a的值以及甲骑车走过的总路程.(写出必要的演算和推理过程)
1.把下面画函数y=-x+2的图象的过程补充完整.
解:(1)列表为:
x
…
-2
-1
0
1
2
3
…
y=-x+2
…
…
(2)画出的函数图象为:
图5
2.周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图6所示,下列说法中正确的是( )
A.小涛家离报亭的距离是900 m
B.小涛从家去报亭的平均速度是60 m/min
C.小涛从报亭返回家中的平均速度是80 m/min
D.小涛在报亭看报用了15 min
图6
图7
3.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t的函数关系图象如图7所示,则休息后园林队每小时绿化面积为________平方米.
4.2018年五一劳动节期间,小张和朋友驾车自助旅游,如图8中的图象描述了小张驾驶的汽车离出发地的路程s(千米)和行驶所用时间t(时)之间的函数关系,请你根据图象,提供小张和朋友驾车自助旅游中的一些具体信息.(至少提供3条与图中的图象有关的信息)
图8
5.“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打6折,设购买种子数量为x(千克),付款金额为y(元),则y与x的函数关系的图象大致是( )
图9
6. “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终赢得比赛,下列函数图象可以体现这一故事过程的是( )
图10
图11
7.将一盛有部分水的圆柱形小玻璃杯固定在事先没有水的大圆柱形容器底部,现用一注水管沿大容器内壁匀速注水(如图11所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
图12
图13
8.小亮家与姥姥家相距24 km,小亮8:00从家出发,骑自行车去姥姥家,妈妈8:30从家出发,乘车沿相同路线去姥姥家,小亮和妈妈的行进路程s(km)与时间t(h)的函数图象如图13所示,则下列说法中错误的有( )
①小亮骑自行车的平均速度是12 km/h;
②妈妈比小亮提前0.5 h到达姥姥家;
③妈妈在距家12 km处追上小亮;
④9:30妈妈追上小亮.
A.1个 B.2个
C.3个 D.4个
9.图14是小明从学校回到家里行进的路程s(米)与时间t(分)的函数图象.观察图象,从中得到如下信息:①学校离小明家1000米;②小明用了20分钟到家;③小明前10分钟走了路程的一半;④小明后10分钟比前10分钟走得快.其中正确的有__________.(填序号)
图14
图15
10.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图15所示,当乙到达终点A时,甲还需________分钟到达终点B.
11.有一个水箱,它的容积是500 L,水箱内原有水200 L,现需将水箱注满,已知每分钟注水10 L.
(1)写出水箱内水量Q(L)与时间t(min)的函数关系式;
(2)求出自变量的取值范围;
(3)画出Q关于t的函数关系图象.
12.如图16所示,A,B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程s(千米)与该日下午时间t(时)之间的关系.
根据图象回答下列问题:
(1)甲和乙哪一个出发得更早?早出发多长时间?
(2)甲和乙哪一个更早到达B地,早多长时间?
(3)描述一下甲的运动情况;
(4)请你根据图象上的数据,分别求出乙骑摩托车的速度和甲骑自行车在全程的平均速度.
图16
13.汽车在行驶过程中,速度往往是变化的,下图图象表示的是一辆汽车的速度随时间变化而变化的情况.
汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
汽车在哪些时间段保持匀速行驶?时速分别是多少?
出发后8分钟到10分钟之间可能发生了什么情况?
14.甲、乙两人(甲骑自行车,乙骑摩托车)从A城出发到B地旅行,如图表示甲、乙两人离开A城的路程与时间之间的函数图象.根据图象,你能得到关于甲、乙两人旅行的哪些信息?
答题要求:(1)请至少提供四条信息,如,由图象可知:甲比乙早出发4小时;甲离开A城的路程与时间的函数图象是一条折线段,说明甲作变速运动.
(2)不要再提供“(1)”中已列举的信息:① ;② ;③ ;④ .
15.甲、乙、丙三人同时从A村出发去B村,刚开始甲骑自行车载乙,丙步行;a小时后甲骑车中途回头接丙,乙步行,结果三人同时到达B地.假设:乙、丙步行速度相同,甲载乙与甲载丙时速度相同,甲载人与不载人时的速度不同,甲、乙、丙三人与A村之间的距离y(千米)与出发的时间x(小时)之间的函数关系如图.(掉头与上下车时间忽略不计)
(1)选择:
甲与A村之间的距离y(千米)与出发时间x(小时)之间的函数图象为折线( )
A、O-M-P??? ?B、O-N-P?? ? C、O-M-N-P???? D、O-N-M-P
乙与A村之间的距离y(千米)与出发时间x(小时)之间的函数图象为折线( )
A、O-M-P???? B、O-N-P???? C、O-M-N-P???? D、O-N-M-P
丙与A村之间的距离y(千米)与出发时间x(小时)之间的函数图象为折线( )
A、O-M-P???? B、O-N-P???? C、O-M-N-P???? D、O-N-M-P
(2)求步行速度,和甲载人骑车时的速度;
(3)求a的值以及甲骑车走过的总路程.(写出必要的演算和推理过程)
