人教版高一数学必修四2.4.1平面向量数量积的物理背景及其含义课件 共22张PPT
文档属性
| 名称 | 人教版高一数学必修四2.4.1平面向量数量积的物理背景及其含义课件 共22张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-21 07:09:50 | ||
图片预览







文档简介
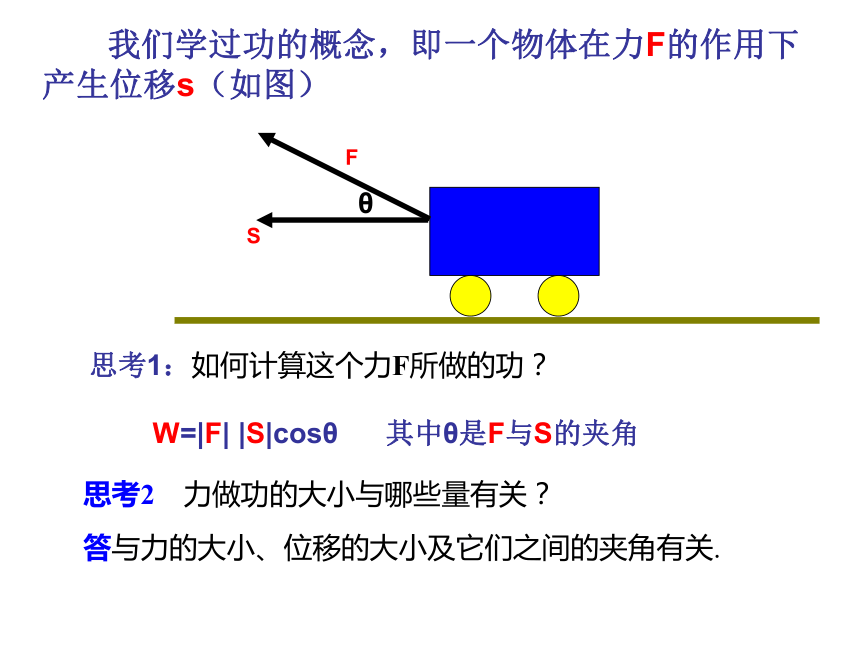
课件22张PPT。 我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)θFS思考1:如何计算这个力F所做的功?
W=|F| |S|cosθ 其中θ是F与S的夹角 思考2 力做功的大小与哪些量有关? 答与力的大小、位移的大小及它们之间的夹角有关.思考3 用文字语言表达功的计算公式 W=|F| |S|cosθ 答:功是力与位移的大小及其夹角的余弦的乘积思考4 如果将公式中的力与位移推广到一般向量,其结果又如何表达?答:两个向量的大小及夹角余弦的乘积 2.4.1 平面向量数量积的物理
背景及其含义(一)第二章 § 2.4 平面向量的数量积1.了解平面向量数量积的物理背景,即物体在力F的作用下产生位移s所做的功.
2.掌握平面向量数量积的定义和运算律,理解其几何意义.
3.会用两个向量的数量积求两个向量的夹角以及判断两个向量是否垂直.学习目标定
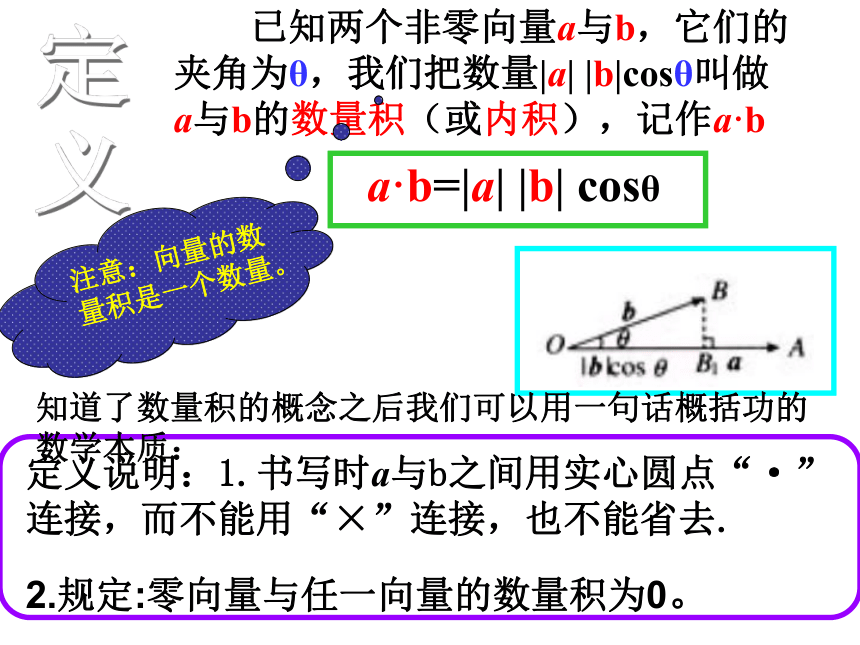
义注意:向量的数量积是一个数量。知道了数量积的概念之后我们可以用一句话概括功的数学本质:思考1 向量的数量积运算结果和向量的线性运算的结果有什么区别?答 向量的线性运算结果是向量,而向量的数量积是数量.思考2 非零向量的数量积是否可为正数,负数和零,其数量积的符号由什么来决定的?答案概念升华B类型一 平面向量数量积的含义求平面向量数量积的步骤是:
(1)分别求|a|和|b|;
(2)求a与b的夹角θ,θ∈[0,π] ;
(3)求数量积,即a·b=|a||b|cos θ,要特别注意书写时a与b之间用实心圆点“·”连接,而不能用“×”连接,也不能省去.总结归纳题型探究 解析答案变式 已知|a|=4,|b|=5;
(1)当a⊥b时,求a与b的数量积.反思与感悟(2)当a∥b时,求a与b的数量积.
(3)当a与b的夹角为60°时,求a与b的数量积. (4)当a·b=10时,求a与b的夹角.解 (1)a∥b,若a与b同向,则θ=0°,
a·b=|a|·|b|cos 0°=4×5=20;
若a与b反向,则θ=180°,
∴a·b=|a|·|b|cos 180°=4×5×(-1)=-20.
(2)当a⊥b时,θ=90°,∴a·b=|a|·|b|cos 90°=0.
(3)当a与b的夹角为60°时,a·b=|a|·|b|cos 60°知识点三、平面向量数量积的性质|a||b|-|a||b|≤返回答案|a|2(1)a⊥b?
设a与b均为非空向量:
a·b=0一个物体,在力f的作用下产生位移S,如图.?
问题1:力 f 在位移S方向上的分力的数值是多少?
提示:|f|cos θ.问题3:向量b在a方向上的大小是多少?向量a在b方向上的大小?
提示:|b|cosθ; |a|cos θ
问题2:功又可以表述为?
提示:力 f 在位移S方向上的分力大小与位移大小的乘积师生合作探究 1.投影的概念
叫做向量b在a方向上的投影. 叫做向量a在b方向上的投影.
2.数量积的几何意义
a·b的几何意义是 与b在a方向上的投影
的乘积.|b|cosθ|a|cos θ|b|cos θa的长度|a|解析答案类型二 投影
例2 设非零向量a和b,它们的夹角为θ.
(1)若|a|=5,θ=150°,求a在b方向上的投影;(2)若a·b=9,|a|=6,求b在a方向上的投影.题型探究 求投影方法
(1)b在a方向上的投影为|b|cos θ(θ为a,b的夹角),a在b方向上的投影为|a|cos θ.2、平面向量的数量积的运算律:注:合作探究 合作探究:我们知道,对任意 ,恒有类型三 平面向量数量积的运算律反思与感悟解析答案例3 已知| a |=6,|b|=4, a与b的夹角θ=60°,求a ·b。变式 已知| a |=6,|b|=4, a与b的夹角θ=60°,求(a +b) ·(a -b)。变式 已知| a |=6,|b|=4, a与b的夹角θ=60°,求(a +2b) ·(a -3b)。题型探究 例4.已知 ,且 与 不共线,k为何值时,
向量 与 互相垂直。1.了解平面向量数量积的物理背景,即物体在力F的作用下产生位移s所做的功.
2.掌握平面向量数量积的定义和运算律,理解其几何意义.
3.会用两个向量的数量积求两个向量的夹角以及判断两个向量是否垂直.学习目标你完成了吗?课堂随练:
W=|F| |S|cosθ 其中θ是F与S的夹角 思考2 力做功的大小与哪些量有关? 答与力的大小、位移的大小及它们之间的夹角有关.思考3 用文字语言表达功的计算公式 W=|F| |S|cosθ 答:功是力与位移的大小及其夹角的余弦的乘积思考4 如果将公式中的力与位移推广到一般向量,其结果又如何表达?答:两个向量的大小及夹角余弦的乘积 2.4.1 平面向量数量积的物理
背景及其含义(一)第二章 § 2.4 平面向量的数量积1.了解平面向量数量积的物理背景,即物体在力F的作用下产生位移s所做的功.
2.掌握平面向量数量积的定义和运算律,理解其几何意义.
3.会用两个向量的数量积求两个向量的夹角以及判断两个向量是否垂直.学习目标定
义注意:向量的数量积是一个数量。知道了数量积的概念之后我们可以用一句话概括功的数学本质:思考1 向量的数量积运算结果和向量的线性运算的结果有什么区别?答 向量的线性运算结果是向量,而向量的数量积是数量.思考2 非零向量的数量积是否可为正数,负数和零,其数量积的符号由什么来决定的?答案概念升华B类型一 平面向量数量积的含义求平面向量数量积的步骤是:
(1)分别求|a|和|b|;
(2)求a与b的夹角θ,θ∈[0,π] ;
(3)求数量积,即a·b=|a||b|cos θ,要特别注意书写时a与b之间用实心圆点“·”连接,而不能用“×”连接,也不能省去.总结归纳题型探究 解析答案变式 已知|a|=4,|b|=5;
(1)当a⊥b时,求a与b的数量积.反思与感悟(2)当a∥b时,求a与b的数量积.
(3)当a与b的夹角为60°时,求a与b的数量积. (4)当a·b=10时,求a与b的夹角.解 (1)a∥b,若a与b同向,则θ=0°,
a·b=|a|·|b|cos 0°=4×5=20;
若a与b反向,则θ=180°,
∴a·b=|a|·|b|cos 180°=4×5×(-1)=-20.
(2)当a⊥b时,θ=90°,∴a·b=|a|·|b|cos 90°=0.
(3)当a与b的夹角为60°时,a·b=|a|·|b|cos 60°知识点三、平面向量数量积的性质|a||b|-|a||b|≤返回答案|a|2(1)a⊥b?
设a与b均为非空向量:
a·b=0一个物体,在力f的作用下产生位移S,如图.?
问题1:力 f 在位移S方向上的分力的数值是多少?
提示:|f|cos θ.问题3:向量b在a方向上的大小是多少?向量a在b方向上的大小?
提示:|b|cosθ; |a|cos θ
问题2:功又可以表述为?
提示:力 f 在位移S方向上的分力大小与位移大小的乘积师生合作探究 1.投影的概念
叫做向量b在a方向上的投影. 叫做向量a在b方向上的投影.
2.数量积的几何意义
a·b的几何意义是 与b在a方向上的投影
的乘积.|b|cosθ|a|cos θ|b|cos θa的长度|a|解析答案类型二 投影
例2 设非零向量a和b,它们的夹角为θ.
(1)若|a|=5,θ=150°,求a在b方向上的投影;(2)若a·b=9,|a|=6,求b在a方向上的投影.题型探究 求投影方法
(1)b在a方向上的投影为|b|cos θ(θ为a,b的夹角),a在b方向上的投影为|a|cos θ.2、平面向量的数量积的运算律:注:合作探究 合作探究:我们知道,对任意 ,恒有类型三 平面向量数量积的运算律反思与感悟解析答案例3 已知| a |=6,|b|=4, a与b的夹角θ=60°,求a ·b。变式 已知| a |=6,|b|=4, a与b的夹角θ=60°,求(a +b) ·(a -b)。变式 已知| a |=6,|b|=4, a与b的夹角θ=60°,求(a +2b) ·(a -3b)。题型探究 例4.已知 ,且 与 不共线,k为何值时,
向量 与 互相垂直。1.了解平面向量数量积的物理背景,即物体在力F的作用下产生位移s所做的功.
2.掌握平面向量数量积的定义和运算律,理解其几何意义.
3.会用两个向量的数量积求两个向量的夹角以及判断两个向量是否垂直.学习目标你完成了吗?课堂随练:
