高中数学新人教A版必修1第三章函数的应用3.1函数与方程3.1.1方程的根与函数的零点课件24张
文档属性
| 名称 | 高中数学新人教A版必修1第三章函数的应用3.1函数与方程3.1.1方程的根与函数的零点课件24张 |  | |
| 格式 | pptx | ||
| 文件大小 | 780.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-21 13:59:49 | ||
图片预览








文档简介
(共24张PPT)
第三章 函数的应用
3.1 函数与方程
3.1.1 方程的根与函数的零点
1.理解函数零点的定义以及函数零点与方程根的关系,会求函数的零点.
2.掌握函数零点的判定方法.
3.会用函数零点的存在性定理判断函数是否存在零点.
1
2
3
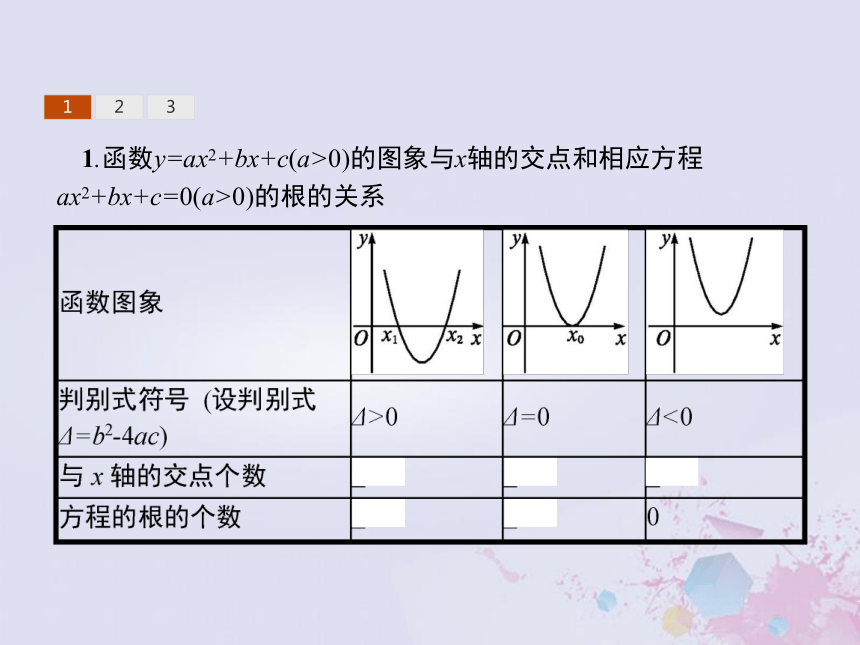
1.函数y=ax2+bx+c(a>0)的图象与x轴的交点和相应方程ax2+bx+c=0(a>0)的根的关系
1
2
3
【做一做1】 已知二次函数y=x2-x-1,则使y=0成立的实数x有( )
A.0个 B.1个
C.2个 D.无数个
解析:判别式Δ=1+4=5>0,则方程x2-x-1=0有两个不相等的实数根,即使y=0成立的实数x有2个.
答案:C
1
2
3
2.函数的零点
(1)定义:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
(2)几何意义:函数y=f(x)的图象与x轴的交点的横坐标就是函数y=f(x)的零点.
(3)结论:方程f(x)=0有实数根 函数y=f(x)的图象与x轴有交点 函数y=f(x)有零点.
名师点拨并非所有的函数都有零点.例如,函数f(x)=x2+1,由于方程x2+1=0无实数根,故该函数无零点.
1
2
3
【做一做2-1】 已知函数y=f(x)有零点,下列说法不正确的是( )
A.f(0)=0
B.方程f(x)=0有实根
C.函数f(x)的图象与x轴有交点
D.函数f(x)的零点是方程f(x)=0的实数根
答案:A
1
2
3
3.函数零点的判定定理
名师点拨判断函数y=f(x)是否存在零点的方法:
(1)方程法:判断方程f(x)=0是否有实数解.
(2)图象法:判断函数y=f(x)的图象与x轴是否有交点.
(3)定理法:利用零点的判定定理来判断.
1
2
3
【做一做3-1】 函数f(x)=x2+x-b2的零点个数是( )
A.0 B.1 C.2 D.无数
解析:∵关于x的一元二次方程x2+x-b2=0的根的判别式Δ=1+4b2>0,∴函数f(x)=x2+x-b2有2个零点.
答案:C
【做一做3-2】 若函数f(x)=kx-2x在(0,1)内有零点,则实数k的取值范围是 .
解析:∵f(x)=kx-2x在(0,1)内有零点,
∴y1=kx与y2=2x的图象在(0,1)内有交点.画出
y2=2x在(0,1)内的图象,如图,又知y1=kx过原点,
故可知k>2时,y1与y2在(0,1)内有交点.
答案:(2,+∞)
1.对零点判定定理的理解
剖析:(1)当函数y=f(x)同时满足:①函数的图象在闭区间[a,b]上是连续曲线;②f(a)·f(b)<0,则可以判断函数y=f(x)在区间(a,b)内至少有一个零点,但是不能明确说明有几个零点.
(2)当函数y=f(x)的图象在闭区间[a,b]上不是连续曲线,或不满足f(a)·f(b)<0时,函数y=f(x)在区间[a,b]上可能存在零点,也可能不存在零点.
例如:二次函数f(x)=x2-2x-3在区间[3,4]上有f(3)=0,f(4)>0,所以f(3)·f(4)=0,但x=3是函数f(x)的一个零点.
函数f(x)=x2在区间[-1,1]上有f(-1)·f(1)=1>0,但是它存在零点0.
2.函数的零点不是点
剖析:我们把使f(x)=0成立的实数x叫做函数y=f(x)的零点,因此函数的零点不是点,是函数y=f(x)的图象与x轴的交点的横坐标,即零点是一个实数.当函数的自变量取这一实数时,其函数值为零.函数f(x)的零点是方程f(x)=0的实根,方程f(x)=0有几个实根,函数f(x)就有几个零点.例如,函数f(x)=x+1,当f(x)=x+1=0成立时,x=-1,所以函数f(x)=x+1有一个零点-1,由此可见,函数f(x)=x+1的零点是一个实数,而不是一个点.
题型一
题型二
题型三
题型四
题型一
题型二
题型三
题型四
题型一
题型二
题型三
题型四
反思1.求函数f(x)的零点时,可考虑解方程f(x)=0,方程f(x)=0无实数根,则函数f(x)无零点,方程f(x)=0有实数根,则方程的实数根是函数f(x)的零点.
2.本例(4)小题中容易错写成函数的零点是x=-6和x=2,其原因是没有验根.
题型一
题型二
题型三
题型四
【变式训练1】 已知函数f(x)=x2+ax+b的零点是-1和-2,则函数g(x)=bx-a的零点为 .
解析:由已知得-1和-2是方程x2+ax+b=0的根,
∴a=3,b=2,∴g(x)=2x-3.
令g(x)=2x-3=0,解得x=log23,故函数g(x)的零点为log23.
答案:log23
题型一
题型二
题型三
题型四
题型一
题型二
题型三
题型四
反思当无法解方程f(x)=0时,常用图象法判断函数f(x)的零点个数.
对于函数f(x),如果能化为f(x)=g(x)-h(x)的形式,其中函数g(x)和h(x)的图象能够画出来,那么在同一平面直角坐标系中画出函数g(x)和h(x)的图象,它们图象交点的个数就是函数f(x)的零点的个数.
题型一
题型二
题型三
题型四
题型一
题型二
题型三
题型四
【例3】方程log3x+x=3的解所在的区间为( )
A.(0,2) B.(1,2) C.(2,3) D.(3,4)
解析:构造函数,转化为确定函数的零点所在的区间.令f(x)=log3x+x-3,则f(1)=log31+1-3=-2<0,f(2)=log32+2-3=logf(3)=log33+3-3=1>0,f(4)=log34+4-3=log312>0,那么方程log3x+x=3的解所在的区间为(2,3).
答案:C
反思判断方程的解所在的区间常转化为函数的零点问题,当无法解方程f(x)=0时,常用函数零点的判定定理来解决.
题型一
题型二
题型三
题型四
【变式训练3】 根据表格中的数据,可以断定方程ex-2x-5=0的一个根所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
解析:设f(x)=ex-2x-5,此函数的图象是连续不断的,由表可知f(0)=1-5=-4<0,f(1)=2.72-7=-4.28<0,f(2)=7.39-9=-1.61<0,f(3)=20.09-11=9.09>0,f(4)=54.60-13=41.60>0,所以f(2)·f(3)<0,所以函数f(x)的一个零点,即方程ex-2x-5=0的一个根所在的区间是(2,3).
答案:C
题型一
题型二
题型三
题型四
易错点 对函数零点的判定定理理解不透彻
【例4】 已知函数y=f(x)的图象在闭区间[a,b]上为一条连续的曲线,且f(a)·f(b)>0,则函数f(x)在(a,b)内( )
A.肯定没有零点
B.至多有一个零点
C.可能有两个零点
D.以上说法均不正确
错解:根据函数零点的判定定理可知,选A.
错因分析:当函数在闭区间[a,b]上为一条连续的曲线,且当f(a)·f(b)<0时,函数在(a,b)内至少存在一个零点.但是若不满足上述条件中的任何一个,则函数未必不存在零点.
题型一
题型二
题型三
题型四
正解:不妨设y=f(x)=x2-1,区间[a,b]为[-2,2],则f(-2)·f(2)>0,但是y=f(x)在区间(-2,2)内存在两个零点-1,1,则可以排除选项A,B,D,故选C.
题型一
题型二
题型三
题型四
A.0 B.1 C.2 D.3
解析:函数f(x)的定义域为{x|x∈R,且x≠0}.
当x>0时,f(x)>0,f(x)=0无实根;
当x<0时,f(x)<0,f(x)=0无实根.
综上,函数f(x)没有零点.
答案:A
第三章 函数的应用
3.1 函数与方程
3.1.1 方程的根与函数的零点
1.理解函数零点的定义以及函数零点与方程根的关系,会求函数的零点.
2.掌握函数零点的判定方法.
3.会用函数零点的存在性定理判断函数是否存在零点.
1
2
3
1.函数y=ax2+bx+c(a>0)的图象与x轴的交点和相应方程ax2+bx+c=0(a>0)的根的关系
1
2
3
【做一做1】 已知二次函数y=x2-x-1,则使y=0成立的实数x有( )
A.0个 B.1个
C.2个 D.无数个
解析:判别式Δ=1+4=5>0,则方程x2-x-1=0有两个不相等的实数根,即使y=0成立的实数x有2个.
答案:C
1
2
3
2.函数的零点
(1)定义:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
(2)几何意义:函数y=f(x)的图象与x轴的交点的横坐标就是函数y=f(x)的零点.
(3)结论:方程f(x)=0有实数根 函数y=f(x)的图象与x轴有交点 函数y=f(x)有零点.
名师点拨并非所有的函数都有零点.例如,函数f(x)=x2+1,由于方程x2+1=0无实数根,故该函数无零点.
1
2
3
【做一做2-1】 已知函数y=f(x)有零点,下列说法不正确的是( )
A.f(0)=0
B.方程f(x)=0有实根
C.函数f(x)的图象与x轴有交点
D.函数f(x)的零点是方程f(x)=0的实数根
答案:A
1
2
3
3.函数零点的判定定理
名师点拨判断函数y=f(x)是否存在零点的方法:
(1)方程法:判断方程f(x)=0是否有实数解.
(2)图象法:判断函数y=f(x)的图象与x轴是否有交点.
(3)定理法:利用零点的判定定理来判断.
1
2
3
【做一做3-1】 函数f(x)=x2+x-b2的零点个数是( )
A.0 B.1 C.2 D.无数
解析:∵关于x的一元二次方程x2+x-b2=0的根的判别式Δ=1+4b2>0,∴函数f(x)=x2+x-b2有2个零点.
答案:C
【做一做3-2】 若函数f(x)=kx-2x在(0,1)内有零点,则实数k的取值范围是 .
解析:∵f(x)=kx-2x在(0,1)内有零点,
∴y1=kx与y2=2x的图象在(0,1)内有交点.画出
y2=2x在(0,1)内的图象,如图,又知y1=kx过原点,
故可知k>2时,y1与y2在(0,1)内有交点.
答案:(2,+∞)
1.对零点判定定理的理解
剖析:(1)当函数y=f(x)同时满足:①函数的图象在闭区间[a,b]上是连续曲线;②f(a)·f(b)<0,则可以判断函数y=f(x)在区间(a,b)内至少有一个零点,但是不能明确说明有几个零点.
(2)当函数y=f(x)的图象在闭区间[a,b]上不是连续曲线,或不满足f(a)·f(b)<0时,函数y=f(x)在区间[a,b]上可能存在零点,也可能不存在零点.
例如:二次函数f(x)=x2-2x-3在区间[3,4]上有f(3)=0,f(4)>0,所以f(3)·f(4)=0,但x=3是函数f(x)的一个零点.
函数f(x)=x2在区间[-1,1]上有f(-1)·f(1)=1>0,但是它存在零点0.
2.函数的零点不是点
剖析:我们把使f(x)=0成立的实数x叫做函数y=f(x)的零点,因此函数的零点不是点,是函数y=f(x)的图象与x轴的交点的横坐标,即零点是一个实数.当函数的自变量取这一实数时,其函数值为零.函数f(x)的零点是方程f(x)=0的实根,方程f(x)=0有几个实根,函数f(x)就有几个零点.例如,函数f(x)=x+1,当f(x)=x+1=0成立时,x=-1,所以函数f(x)=x+1有一个零点-1,由此可见,函数f(x)=x+1的零点是一个实数,而不是一个点.
题型一
题型二
题型三
题型四
题型一
题型二
题型三
题型四
题型一
题型二
题型三
题型四
反思1.求函数f(x)的零点时,可考虑解方程f(x)=0,方程f(x)=0无实数根,则函数f(x)无零点,方程f(x)=0有实数根,则方程的实数根是函数f(x)的零点.
2.本例(4)小题中容易错写成函数的零点是x=-6和x=2,其原因是没有验根.
题型一
题型二
题型三
题型四
【变式训练1】 已知函数f(x)=x2+ax+b的零点是-1和-2,则函数g(x)=bx-a的零点为 .
解析:由已知得-1和-2是方程x2+ax+b=0的根,
∴a=3,b=2,∴g(x)=2x-3.
令g(x)=2x-3=0,解得x=log23,故函数g(x)的零点为log23.
答案:log23
题型一
题型二
题型三
题型四
题型一
题型二
题型三
题型四
反思当无法解方程f(x)=0时,常用图象法判断函数f(x)的零点个数.
对于函数f(x),如果能化为f(x)=g(x)-h(x)的形式,其中函数g(x)和h(x)的图象能够画出来,那么在同一平面直角坐标系中画出函数g(x)和h(x)的图象,它们图象交点的个数就是函数f(x)的零点的个数.
题型一
题型二
题型三
题型四
题型一
题型二
题型三
题型四
【例3】方程log3x+x=3的解所在的区间为( )
A.(0,2) B.(1,2) C.(2,3) D.(3,4)
解析:构造函数,转化为确定函数的零点所在的区间.令f(x)=log3x+x-3,则f(1)=log31+1-3=-2<0,f(2)=log32+2-3=logf(3)=log33+3-3=1>0,f(4)=log34+4-3=log312>0,那么方程log3x+x=3的解所在的区间为(2,3).
答案:C
反思判断方程的解所在的区间常转化为函数的零点问题,当无法解方程f(x)=0时,常用函数零点的判定定理来解决.
题型一
题型二
题型三
题型四
【变式训练3】 根据表格中的数据,可以断定方程ex-2x-5=0的一个根所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
解析:设f(x)=ex-2x-5,此函数的图象是连续不断的,由表可知f(0)=1-5=-4<0,f(1)=2.72-7=-4.28<0,f(2)=7.39-9=-1.61<0,f(3)=20.09-11=9.09>0,f(4)=54.60-13=41.60>0,所以f(2)·f(3)<0,所以函数f(x)的一个零点,即方程ex-2x-5=0的一个根所在的区间是(2,3).
答案:C
题型一
题型二
题型三
题型四
易错点 对函数零点的判定定理理解不透彻
【例4】 已知函数y=f(x)的图象在闭区间[a,b]上为一条连续的曲线,且f(a)·f(b)>0,则函数f(x)在(a,b)内( )
A.肯定没有零点
B.至多有一个零点
C.可能有两个零点
D.以上说法均不正确
错解:根据函数零点的判定定理可知,选A.
错因分析:当函数在闭区间[a,b]上为一条连续的曲线,且当f(a)·f(b)<0时,函数在(a,b)内至少存在一个零点.但是若不满足上述条件中的任何一个,则函数未必不存在零点.
题型一
题型二
题型三
题型四
正解:不妨设y=f(x)=x2-1,区间[a,b]为[-2,2],则f(-2)·f(2)>0,但是y=f(x)在区间(-2,2)内存在两个零点-1,1,则可以排除选项A,B,D,故选C.
题型一
题型二
题型三
题型四
A.0 B.1 C.2 D.3
解析:函数f(x)的定义域为{x|x∈R,且x≠0}.
当x>0时,f(x)>0,f(x)=0无实根;
当x<0时,f(x)<0,f(x)=0无实根.
综上,函数f(x)没有零点.
答案:A
