高中数学新人教A版必修1第三章函数的应用3.2函数模型及其应用3.2.1几类不同增长的函数模型课件21张
文档属性
| 名称 | 高中数学新人教A版必修1第三章函数的应用3.2函数模型及其应用3.2.1几类不同增长的函数模型课件21张 |  | |
| 格式 | zip | ||
| 文件大小 | 485.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-21 14:09:05 | ||
图片预览







文档简介
课件21张PPT。3.2 函数模型及其应用3.2.1 几类不同增长的函数模型1.利用计算工具,比较指数函数、对数函数以及幂函数的增长差异.
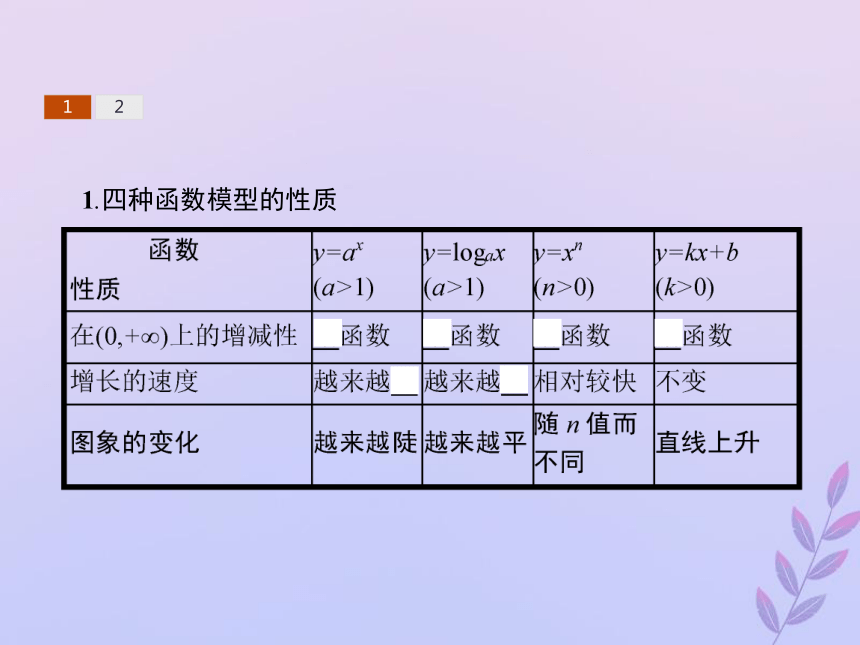
2.结合实例体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义.121.四种函数模型的性质 12【做一做1】 函数y=2x与y=x2的图象的交点个数是 ( )
A.0 B.1 C.2 D.3
解析:作出两个函数的图象,在第一象限中有2个交点,在第二象限中有1个交点,即共有3个交点.
答案:D122.三种增长函数模型的比较
(1)指数函数和幂函数.
一般地,对于指数函数y=ax(a>1)和幂函数y=xn(n>0),通过探索可以发现,在区间(0,+∞)内,无论n比a大多少,尽管在x的一定变化范围内,ax会小于xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn.
(2)对数函数和幂函数.
对于对数函数y=logax(a>1)和幂函数y=xn(n>0),在区间(0,+∞)内,随着x的增大,logax增长得越来越慢,图象就像是渐渐地与x轴平行一样.尽管在x的一定变化范围内,logax可能会大于xn,但由于logax的增长慢于xn的增长,因此总存在一个x0,当x>x0时,就会有logax在区间(0,+∞)内,尽管函数y=ax(a>1),y=logax(a>1)和y=xn(n>0)都是增函数,但它们的增长速度不同,而且不在同一个“档次”上.随着x的增大,y=ax(a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而y=logax(a>1)的增长速度则会越来越慢.因此,总会存在一个x0,当x>x0时,就有logax【做一做2】 当x>4时,a=4x,b=log4x,c=x4,则有( )
A.aC.c答案:D几类常见函数模型的增长特点
剖析:(1)直线模型:即一次函数模型y=kx+b(k≠0).现实生活中很多事例可以用直线模型表示,例如,匀速直线运动的时间和位移的关系,弹簧的伸长与拉力的关系等.直线模型的增长特点是直线上升(x的系数k>0),通过图象可以很直观地认识它.
(2)指数函数模型:能用指数型函数表达的函数模型y=k·ax+b(k≠0)叫做指数函数模型.指数函数增长的特点是随着自变量的增大,函数值增大的速度越来越快(底数a>1,ax的系数k>0),常形象地称之为“指数爆炸”.通过细胞分裂的实例以及函数图象的变化都可以清楚地看到“指数爆炸”的威力.
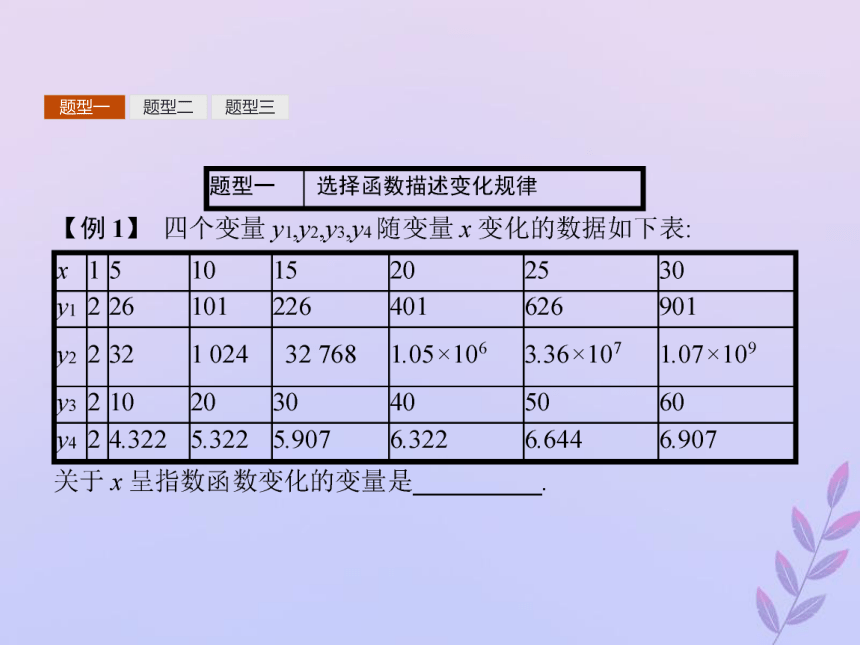
(3)对数函数模型:能用对数函数表达的函数模型y=klogax+b(k≠0)叫做对数函数模型.对数函数增长的特点是随着自变量的增大(底数a>1,logax的系数k>0),函数值增大的速度越来越慢.题型一题型二题型三题型一题型二题型三解析:以爆炸式增长的变量是呈指数函数变化的.从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,变量y1,y2,y3,y4都是越来越大,但是增长速度不同,其中变量y2的增长速度最快,可知变量y2关于x呈指数函数变化.
答案:y2
反思选择函数描述变化规律时,当增长速度最快且呈“爆炸”式增长时,常选择指数函数模型来描述;当增长速度较慢时,常选择对数函数模型来描述;当增长速度相对平稳时,常选择幂函数模型来描述;当增长的速度不变时,常选择一次函数模型来描述.题型一题型二题型三题型一题型二题型三【例2】 甲、乙、丙三个公司分别到慈善总会捐款给某灾区,捐款方式如下:
甲公司:在10天内,每天捐款5万元给灾区;乙公司:在10天内,第1天捐款1万元,以后每天比前一天多捐款1万元;丙公司:在10天内,第1天捐款0.1万元,以后每天捐款都比前一天翻一番.
你觉得哪个公司最慷慨?
分析:分别计算三个公司在10天内的捐款总数,捐款总数越大的公司越慷慨.题型一题型二题型三题型一题型二题型三由上表可以看出,丙公司捐款最多,为102.3万元,即丙公司最慷慨.
反思解答此类问题的关键是明确“指数爆炸”“对数增长”等函数增长差异,需注意幂函数的增长是介于两者之间的.题型一题型二题型三【变式训练2】 某汽车制造商在2017年初公告:公司计划2017年生产目标定为43万辆.已知该公司近三年的汽车生产量如下表所示:
如果我们分别将2014,2015,2016,2017定义为第一、二、三、四年.现在你有两个函数模型:二次函数模型f(x)=ax2+bx+c(a≠0),指数函数模型g(x)=a·bx+c(a≠0,b>0,b≠1),哪个模型能更好地反映该公司年产量y与年份x的关系?题型一题型二题型三题型一题型二题型三题型一题型二题型三易错点 提取图象信息错误而导致解题错误
【例3】 已知甲、乙两物体在同一直线上向同一方向做匀速直线运动,其位移y(单位:km)和运动时间x(单位:h)
(0≤x≤5)的关系如图所示,给出以下说法:
①甲、乙运动的速度相同,都是5 km/h;
②甲、乙运动的时间相同,开始运动后相等
时间内甲的位移比乙大;
③甲、乙运动的时间相同,乙的速度是4 km/h;
④当甲、乙运动了3h后,甲的位移比乙大3 km,但乙在甲前方2 km处.
其中正确的说法是( )
A.③ B.①②③ C.①③④ D.②③④错解经分析,③是对的,故①错;对于②,因为乙的图象在甲的上方,所以应是甲的位移比乙小,故②错误;对于④,当甲、乙运动了3 h后,甲的位移为3×5=15(km),乙的位移为5+3×4=17(km),故④错误.故选A.
错因分析错解中因对乙出发点的位置理解不准确导致判断②④出错.
正解经分析③是对的,故①错;对于②,甲、乙运动的时间显然都是5 h,因为甲的速度为5 km/h,乙的速度为4 km/h,所以开始运动后相等时间内甲的位移比乙大,故②正确;对于④,当甲、乙运动了3 h后,甲的位移为3×5=15(km),乙的位移为3×4=12(km).又因为乙是从甲前方5 km处开始运动的,所以甲的位移比乙大3 km,但乙在甲前方2 km处,所以④正确,故选D.题型一题型二题型三题型一题型二题型三反思图表型应用问题是高考中一道亮丽的风景线.这类试题应结合图象的特征,观察坐标轴所代表的含义,紧扣题目的语言描述,并把它转化为数学特征(单调性、最值等)即可得到完美的解决.题型一题型二题型三【变式训练3】
甲、乙两人在一次赛跑中,路程s与时间t的函数关系如图所示,则下列说法正确的是( )
A.甲比乙先出发
B.乙比甲跑的路程多
C.甲、乙两人的速度相同
D.甲先到达终点
解析:由图可知,甲与乙同时出发,甲的速度大,甲先到达终点.
答案:D
2.结合实例体会直线上升、指数爆炸、对数增长等不同函数类型增长的含义.121.四种函数模型的性质 12【做一做1】 函数y=2x与y=x2的图象的交点个数是 ( )
A.0 B.1 C.2 D.3
解析:作出两个函数的图象,在第一象限中有2个交点,在第二象限中有1个交点,即共有3个交点.
答案:D122.三种增长函数模型的比较
(1)指数函数和幂函数.
一般地,对于指数函数y=ax(a>1)和幂函数y=xn(n>0),通过探索可以发现,在区间(0,+∞)内,无论n比a大多少,尽管在x的一定变化范围内,ax会小于xn,但由于ax的增长快于xn的增长,因此总存在一个x0,当x>x0时,就会有ax>xn.
(2)对数函数和幂函数.
对于对数函数y=logax(a>1)和幂函数y=xn(n>0),在区间(0,+∞)内,随着x的增大,logax增长得越来越慢,图象就像是渐渐地与x轴平行一样.尽管在x的一定变化范围内,logax可能会大于xn,但由于logax的增长慢于xn的增长,因此总存在一个x0,当x>x0时,就会有logax
A.a
剖析:(1)直线模型:即一次函数模型y=kx+b(k≠0).现实生活中很多事例可以用直线模型表示,例如,匀速直线运动的时间和位移的关系,弹簧的伸长与拉力的关系等.直线模型的增长特点是直线上升(x的系数k>0),通过图象可以很直观地认识它.
(2)指数函数模型:能用指数型函数表达的函数模型y=k·ax+b(k≠0)叫做指数函数模型.指数函数增长的特点是随着自变量的增大,函数值增大的速度越来越快(底数a>1,ax的系数k>0),常形象地称之为“指数爆炸”.通过细胞分裂的实例以及函数图象的变化都可以清楚地看到“指数爆炸”的威力.
(3)对数函数模型:能用对数函数表达的函数模型y=klogax+b(k≠0)叫做对数函数模型.对数函数增长的特点是随着自变量的增大(底数a>1,logax的系数k>0),函数值增大的速度越来越慢.题型一题型二题型三题型一题型二题型三解析:以爆炸式增长的变量是呈指数函数变化的.从表格中可以看出,四个变量y1,y2,y3,y4均是从2开始变化,变量y1,y2,y3,y4都是越来越大,但是增长速度不同,其中变量y2的增长速度最快,可知变量y2关于x呈指数函数变化.
答案:y2
反思选择函数描述变化规律时,当增长速度最快且呈“爆炸”式增长时,常选择指数函数模型来描述;当增长速度较慢时,常选择对数函数模型来描述;当增长速度相对平稳时,常选择幂函数模型来描述;当增长的速度不变时,常选择一次函数模型来描述.题型一题型二题型三题型一题型二题型三【例2】 甲、乙、丙三个公司分别到慈善总会捐款给某灾区,捐款方式如下:
甲公司:在10天内,每天捐款5万元给灾区;乙公司:在10天内,第1天捐款1万元,以后每天比前一天多捐款1万元;丙公司:在10天内,第1天捐款0.1万元,以后每天捐款都比前一天翻一番.
你觉得哪个公司最慷慨?
分析:分别计算三个公司在10天内的捐款总数,捐款总数越大的公司越慷慨.题型一题型二题型三题型一题型二题型三由上表可以看出,丙公司捐款最多,为102.3万元,即丙公司最慷慨.
反思解答此类问题的关键是明确“指数爆炸”“对数增长”等函数增长差异,需注意幂函数的增长是介于两者之间的.题型一题型二题型三【变式训练2】 某汽车制造商在2017年初公告:公司计划2017年生产目标定为43万辆.已知该公司近三年的汽车生产量如下表所示:
如果我们分别将2014,2015,2016,2017定义为第一、二、三、四年.现在你有两个函数模型:二次函数模型f(x)=ax2+bx+c(a≠0),指数函数模型g(x)=a·bx+c(a≠0,b>0,b≠1),哪个模型能更好地反映该公司年产量y与年份x的关系?题型一题型二题型三题型一题型二题型三题型一题型二题型三易错点 提取图象信息错误而导致解题错误
【例3】 已知甲、乙两物体在同一直线上向同一方向做匀速直线运动,其位移y(单位:km)和运动时间x(单位:h)
(0≤x≤5)的关系如图所示,给出以下说法:
①甲、乙运动的速度相同,都是5 km/h;
②甲、乙运动的时间相同,开始运动后相等
时间内甲的位移比乙大;
③甲、乙运动的时间相同,乙的速度是4 km/h;
④当甲、乙运动了3h后,甲的位移比乙大3 km,但乙在甲前方2 km处.
其中正确的说法是( )
A.③ B.①②③ C.①③④ D.②③④错解经分析,③是对的,故①错;对于②,因为乙的图象在甲的上方,所以应是甲的位移比乙小,故②错误;对于④,当甲、乙运动了3 h后,甲的位移为3×5=15(km),乙的位移为5+3×4=17(km),故④错误.故选A.
错因分析错解中因对乙出发点的位置理解不准确导致判断②④出错.
正解经分析③是对的,故①错;对于②,甲、乙运动的时间显然都是5 h,因为甲的速度为5 km/h,乙的速度为4 km/h,所以开始运动后相等时间内甲的位移比乙大,故②正确;对于④,当甲、乙运动了3 h后,甲的位移为3×5=15(km),乙的位移为3×4=12(km).又因为乙是从甲前方5 km处开始运动的,所以甲的位移比乙大3 km,但乙在甲前方2 km处,所以④正确,故选D.题型一题型二题型三题型一题型二题型三反思图表型应用问题是高考中一道亮丽的风景线.这类试题应结合图象的特征,观察坐标轴所代表的含义,紧扣题目的语言描述,并把它转化为数学特征(单调性、最值等)即可得到完美的解决.题型一题型二题型三【变式训练3】
甲、乙两人在一次赛跑中,路程s与时间t的函数关系如图所示,则下列说法正确的是( )
A.甲比乙先出发
B.乙比甲跑的路程多
C.甲、乙两人的速度相同
D.甲先到达终点
解析:由图可知,甲与乙同时出发,甲的速度大,甲先到达终点.
答案:D
