人教版高中数学复习课件:误差知识与算法知识.共47张PPT
文档属性
| 名称 | 人教版高中数学复习课件:误差知识与算法知识.共47张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 361.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-21 22:38:55 | ||
图片预览











文档简介
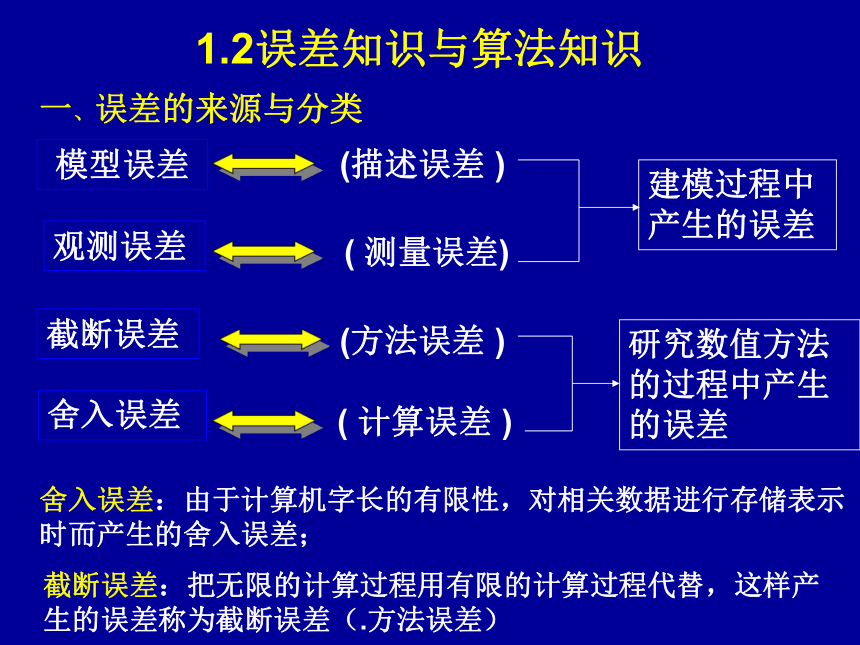
课件47张PPT。 误差知识与算法知识一、误差的来源与分类二、 绝对误差、相对误差与有效数字三、误差估计的基本方法四、算法的计算复杂性五、数值运算中的一些原则 1.2误差知识与算法知识一、误差的来源与分类 模型误差 观测误差 截断误差 (描述误差 )( 测量误差) (方法误差 )( 计算误差 )舍入误差建模过程中
产生的误差研究数值方法
的过程中产生
的误差舍入误差:由于计算机字长的有限性,对相关数据进行存储表示
时而产生的舍入误差;截断误差:把无限的计算过程用有限的计算过程代替,这样产生的误差称为截断误差(.方法误差)二、 绝对误差、相对误差与有效数字(1)绝对误差 (2)相对误差(3)有效数字(4)绝对误差与有效数字的关系(5)相对误差与有效数字的关系二、 绝对误差、相对误差与有效数字(1)绝对误差: (2)相对误差: 马拉松的路程:
42.195公里 二、 绝对误差、相对误差与有效数字(1)绝对误差: (2)相对误差: 相对误差限: 马拉松的路程:
42.195公里 解解解结论:凡是由准确
值经过四舍五入而
得到的近似值,其
绝对误差限等于该
近似值末位的半个
单位。结论:凡是由准确值经过四舍五入而得到的近似值,其绝对误差限等于该近似值末位的半个单位。思考:四舍五入得到的近似值可直接得到其绝对误差限。一般数的近似值能否直接得到其绝对误差限?即希望从近似数的本身显示其精确度。(3)有效数字在测量中,是指在分析工作中实际能够测量到的数字。 所谓能够测量到的是包括最后一位估计的,不确定的数字。 通过直读获得的准确数字叫做可靠数字;通过估读得到的那部分数字叫做存疑数字。
把测量结果中能够反映被测量大小的带有一位存疑数字的全部数字叫有效数字 .在测量中的定义:有效数字=可靠数字+存疑数字(1位)(3)有效数字把测量结果中能够反映被测量大小的带有一位存疑数字的全部数字叫有效数字 .有效数字=可靠数字+存疑数字(1位)a,b的有效数字有几位?(3)有效数字把测量结果中能够反映被测量大小的带有一位存疑数字的全部数字叫有效数字 .有效数字=可靠数字+存疑数字(1位)各有几位有效数字?思考:如何用数学语言描述有效数字?(3)有效数字有效数字的定义:各有几位有效数字?思考:如何用数学语言描述有效数字?(3)有效数字有效数字的定义(描述): 设a是x的近似值,如果a的误差绝对限是x的第k位小数的半个单位,即则称近似值a准确到小数点后第k位。从这个小数点后第k位数字直到最左边非零数字之间的所有数字都叫有效数字。另一种说法(量化):(3)有效数字 设a是x的近似值,如果a的误差绝对限是x的第k位小数的半个单位,即则称近似值a准确到小数点后第k位。从这个小数点后第k位数字直到最左边非零数字之间的所有数字都叫有效数字。有效数字的定义:(3)有效数字 设a是x的近似值,如果a的误差绝对值不超过x的第k位小数的半个单位,即从这个小数点后第k位数字直到最左边非零数字之间的所有数字都叫有效数字。有效数字的定义:例当取3.141作为近似值时,具有几位有效数字?4位3位当取3.142作为近似值时,具有几位有效数字?例当取3.142作为近似值时,具有几位有效数字?当取3.141作为近似值时,具有几位有效数字?4位3位思考:经四舍五入得到的数的有效数字如何确定?(1)若a是经过四舍五入而得到的近似值,则从它的末位
数字到第一位非零数字都是有效数字。思考:取作为的近似值有几位有效数字?有几位有效数字?(1)若a是经过四舍五入而得到的近似值,则从它的末位
数字到第一位非零数字都是有效数字。(2)将任何数乘以 等于移动该数的小
数点,并不影响其有效数字.有效数字与小数点的位置无关。有效数字零不能丢掉:如0.2,0.20,0.200思考:取作为的近似值有几位有效数字?有几位有效数字? 设数x的近似值用科学计数法表示为:思考:其中m是整数,是0,1,2,…,9中的任一数,但若 则 具有几位有效数字? 设数x的近似值其中m是整数,是0,1,2,…,9中的任一数,但若定义: 则称 具有k位有效数字。为有效数字。有效数字的第二种定义(科学计数法意义下有效数字的定义): 设数x的近似值其中m是整数,是0,1,2,…,9中的任一数,但若则具有k位有效数字.(3)有效数字有效数字的含义:有效数字的位数相当于
相对误差大约为 分子1(1)若a是经过四舍五入而得到的近似值,则从它的末位
数字到第一位非零数字都是有效数字。几点说明:(2)将任何数乘以 等于移动该数的小
数点,并不影响其有效数字.有效数字与小数点的位置无关。思考:有效数字相同的两个近似数的绝对误差是否相同?有效数字零不能丢掉:如0.2,0.20,0.200(1)若a是经过四舍五入而得到的近似值,则从它的末位
数字到第一位非零数字都是有效数字。几点说明:(2)将任何数乘以 等于移动该数的小
数点,并不影响其有效数字.有效数字与小数点的位置无关。思考:准确值的的有效数字有多少位?.(3)有效数字相同的两个近似数的绝对误差不一定相同。有效数字零不能丢掉:如0.2,0.20,0.200相对误差相同吗?(1)若a是经过四舍五入而得到的近似值,则从它的末位
数字到第一位非零数字都是有效数字。几点说明:(2)将任何数乘以 等于移动该数的小
数点,并不影响其有效数字.有效数字与小数点的位置无关。(4)准确值被认为具有无穷多位有效数字.(3)有效数字相同的两个近似数的绝对误差不一定相同。有效数字零不能丢掉:如0.2,0.20,0.200(4)绝对误差与有效数字的关系有效数字位数越多,绝对误差越小.(5)相对误差与有效数字的关系:若近似数具有n位有效数字 ,则其相对误差一般应用中,可以取相对误差限:有效数字位数越多,相对误差越小.例4 取3.14作为 的四舍五入的近似值时,试求其相
对误差.解: 有效数字位数n=3,例4 取3.14作为 的四舍五入的近似值时,试求其相
对误差.解: 有效数字位数n=3,(5)相对误差与有效数字的关系:★若近似数具有n位有效数字 ,则其相对误差一般应用中,可以取相对误差限:有效数字位数越多,相对误差越小.★若近似数则该近似数至少具有n位有效数字 .李庆阳教材第6页,
定理1(留为作业1)★若近似数的相对误差则该近似数至少具有n位有效数字 .例5 设sin9的近似值x=0.156431的相对误差问x具有几位有效数字?三、误差估计的基本方法如果自变量x被近似值a问题:对于函数代替,将如何估计 的误差?(一)误差估计的一般运算(二)误差估计的四则运算=?(参考任玉杰,12页)三、误差估计的基本方法一元函数: (一)误差估计的一般运算一元函数: 二元函数:(一)误差估计的一般运算三、误差估计的基本方法一元函数: 二元函数:n元函数:三、误差估计的基本方法(二)误差估计的四则运算(自学。作业2)例6 设有三个近似数a=2.31, b=1.93, c=2.24它们都有三位有效数字,试计算并问:p的计算结果能有几位有效数字?教材例4解P=2.31+1.93×2.24=6.6332=0.005+0.005(1.3+2.24)=0.02585p的计算结果至少有2位有效数字四、算法的计算复杂性★算法:有步骤地完成解数值问题的过程。规定了怎样从
输入数据计算出数值问题解的一个有限的基本运算序列。★好算法的标准: (1)有可靠的理论基础,包括正确性、收敛性、数值
稳定性以及可作误差分析。(2)有良好的计算复杂性。★计算复杂性:时间复杂性: 达到给定精度所需计算量。 空间复杂性: 所占的内存空间。 例10 计算多项式的值,输入数据为和x,输出数据为的值.算法一: 加法次数: n乘法次数: 算法二: 加法次数: n乘法次数: n我国古代数学家秦九韶(1202-1261)在1247年首次提出。秦九韶算法 五、数值运算中的一些原则 1、要有数值稳定性 (即能控制舍入误差的传播)例4 在四位十进制的限制下计算积分算法A: 算法B: 2、合理安排量级相差悬殊数间的运算次序,防止 “大数”吃掉“小数”;例5 设有在四位十进制的限制下计算其和 算法A: 从左往右算 ………….....算法B:从右往左算。………….....3、避免两个相近的数相减例6 求二次方程 算法A:利用公式的根 具有1位有效数字 3、避免两个相近的数相减例6 求二次方程 算法A:利用公式的根 具有1位有效数字 算法B:具有3位有效数字 3、避免两个相近的数相减例6 求二次方程 算法A:利用公式的根 具有1位有效数字 算法B:具有3位有效数字 算法C:3、避免两个相近的数相减一元二次方程的计算公式:阅读:
避免两个相近的数相减的常用方法:
参看任玉杰教材19-21页阅读:
避免两个相近的数相减的常用方法:
参看任玉杰教材19-21页(1)倒数变换法:(2)对数变换法:(3)余弦变换法:(4)泰勒级数法:4、避免接近于0的数作除数,防止溢出。5、简化计算步骤,减少运算次数。4、避免接近于0的数作除数,防止溢出。5、简化计算步骤,减少运算次数。 END 五、数值运算中的一些原则 1、要有数值稳定性 (即能控制舍入误差的传播)2、合理安排量级相差悬殊数间的运算次序,防止 “大数”吃掉“小数”;3、避免两个相近的数相减作业5:任玉杰习题1.2、1.3、1.4
产生的误差研究数值方法
的过程中产生
的误差舍入误差:由于计算机字长的有限性,对相关数据进行存储表示
时而产生的舍入误差;截断误差:把无限的计算过程用有限的计算过程代替,这样产生的误差称为截断误差(.方法误差)二、 绝对误差、相对误差与有效数字(1)绝对误差 (2)相对误差(3)有效数字(4)绝对误差与有效数字的关系(5)相对误差与有效数字的关系二、 绝对误差、相对误差与有效数字(1)绝对误差: (2)相对误差: 马拉松的路程:
42.195公里 二、 绝对误差、相对误差与有效数字(1)绝对误差: (2)相对误差: 相对误差限: 马拉松的路程:
42.195公里 解解解结论:凡是由准确
值经过四舍五入而
得到的近似值,其
绝对误差限等于该
近似值末位的半个
单位。结论:凡是由准确值经过四舍五入而得到的近似值,其绝对误差限等于该近似值末位的半个单位。思考:四舍五入得到的近似值可直接得到其绝对误差限。一般数的近似值能否直接得到其绝对误差限?即希望从近似数的本身显示其精确度。(3)有效数字在测量中,是指在分析工作中实际能够测量到的数字。 所谓能够测量到的是包括最后一位估计的,不确定的数字。 通过直读获得的准确数字叫做可靠数字;通过估读得到的那部分数字叫做存疑数字。
把测量结果中能够反映被测量大小的带有一位存疑数字的全部数字叫有效数字 .在测量中的定义:有效数字=可靠数字+存疑数字(1位)(3)有效数字把测量结果中能够反映被测量大小的带有一位存疑数字的全部数字叫有效数字 .有效数字=可靠数字+存疑数字(1位)a,b的有效数字有几位?(3)有效数字把测量结果中能够反映被测量大小的带有一位存疑数字的全部数字叫有效数字 .有效数字=可靠数字+存疑数字(1位)各有几位有效数字?思考:如何用数学语言描述有效数字?(3)有效数字有效数字的定义:各有几位有效数字?思考:如何用数学语言描述有效数字?(3)有效数字有效数字的定义(描述): 设a是x的近似值,如果a的误差绝对限是x的第k位小数的半个单位,即则称近似值a准确到小数点后第k位。从这个小数点后第k位数字直到最左边非零数字之间的所有数字都叫有效数字。另一种说法(量化):(3)有效数字 设a是x的近似值,如果a的误差绝对限是x的第k位小数的半个单位,即则称近似值a准确到小数点后第k位。从这个小数点后第k位数字直到最左边非零数字之间的所有数字都叫有效数字。有效数字的定义:(3)有效数字 设a是x的近似值,如果a的误差绝对值不超过x的第k位小数的半个单位,即从这个小数点后第k位数字直到最左边非零数字之间的所有数字都叫有效数字。有效数字的定义:例当取3.141作为近似值时,具有几位有效数字?4位3位当取3.142作为近似值时,具有几位有效数字?例当取3.142作为近似值时,具有几位有效数字?当取3.141作为近似值时,具有几位有效数字?4位3位思考:经四舍五入得到的数的有效数字如何确定?(1)若a是经过四舍五入而得到的近似值,则从它的末位
数字到第一位非零数字都是有效数字。思考:取作为的近似值有几位有效数字?有几位有效数字?(1)若a是经过四舍五入而得到的近似值,则从它的末位
数字到第一位非零数字都是有效数字。(2)将任何数乘以 等于移动该数的小
数点,并不影响其有效数字.有效数字与小数点的位置无关。有效数字零不能丢掉:如0.2,0.20,0.200思考:取作为的近似值有几位有效数字?有几位有效数字? 设数x的近似值用科学计数法表示为:思考:其中m是整数,是0,1,2,…,9中的任一数,但若 则 具有几位有效数字? 设数x的近似值其中m是整数,是0,1,2,…,9中的任一数,但若定义: 则称 具有k位有效数字。为有效数字。有效数字的第二种定义(科学计数法意义下有效数字的定义): 设数x的近似值其中m是整数,是0,1,2,…,9中的任一数,但若则具有k位有效数字.(3)有效数字有效数字的含义:有效数字的位数相当于
相对误差大约为 分子1(1)若a是经过四舍五入而得到的近似值,则从它的末位
数字到第一位非零数字都是有效数字。几点说明:(2)将任何数乘以 等于移动该数的小
数点,并不影响其有效数字.有效数字与小数点的位置无关。思考:有效数字相同的两个近似数的绝对误差是否相同?有效数字零不能丢掉:如0.2,0.20,0.200(1)若a是经过四舍五入而得到的近似值,则从它的末位
数字到第一位非零数字都是有效数字。几点说明:(2)将任何数乘以 等于移动该数的小
数点,并不影响其有效数字.有效数字与小数点的位置无关。思考:准确值的的有效数字有多少位?.(3)有效数字相同的两个近似数的绝对误差不一定相同。有效数字零不能丢掉:如0.2,0.20,0.200相对误差相同吗?(1)若a是经过四舍五入而得到的近似值,则从它的末位
数字到第一位非零数字都是有效数字。几点说明:(2)将任何数乘以 等于移动该数的小
数点,并不影响其有效数字.有效数字与小数点的位置无关。(4)准确值被认为具有无穷多位有效数字.(3)有效数字相同的两个近似数的绝对误差不一定相同。有效数字零不能丢掉:如0.2,0.20,0.200(4)绝对误差与有效数字的关系有效数字位数越多,绝对误差越小.(5)相对误差与有效数字的关系:若近似数具有n位有效数字 ,则其相对误差一般应用中,可以取相对误差限:有效数字位数越多,相对误差越小.例4 取3.14作为 的四舍五入的近似值时,试求其相
对误差.解: 有效数字位数n=3,例4 取3.14作为 的四舍五入的近似值时,试求其相
对误差.解: 有效数字位数n=3,(5)相对误差与有效数字的关系:★若近似数具有n位有效数字 ,则其相对误差一般应用中,可以取相对误差限:有效数字位数越多,相对误差越小.★若近似数则该近似数至少具有n位有效数字 .李庆阳教材第6页,
定理1(留为作业1)★若近似数的相对误差则该近似数至少具有n位有效数字 .例5 设sin9的近似值x=0.156431的相对误差问x具有几位有效数字?三、误差估计的基本方法如果自变量x被近似值a问题:对于函数代替,将如何估计 的误差?(一)误差估计的一般运算(二)误差估计的四则运算=?(参考任玉杰,12页)三、误差估计的基本方法一元函数: (一)误差估计的一般运算一元函数: 二元函数:(一)误差估计的一般运算三、误差估计的基本方法一元函数: 二元函数:n元函数:三、误差估计的基本方法(二)误差估计的四则运算(自学。作业2)例6 设有三个近似数a=2.31, b=1.93, c=2.24它们都有三位有效数字,试计算并问:p的计算结果能有几位有效数字?教材例4解P=2.31+1.93×2.24=6.6332=0.005+0.005(1.3+2.24)=0.02585p的计算结果至少有2位有效数字四、算法的计算复杂性★算法:有步骤地完成解数值问题的过程。规定了怎样从
输入数据计算出数值问题解的一个有限的基本运算序列。★好算法的标准: (1)有可靠的理论基础,包括正确性、收敛性、数值
稳定性以及可作误差分析。(2)有良好的计算复杂性。★计算复杂性:时间复杂性: 达到给定精度所需计算量。 空间复杂性: 所占的内存空间。 例10 计算多项式的值,输入数据为和x,输出数据为的值.算法一: 加法次数: n乘法次数: 算法二: 加法次数: n乘法次数: n我国古代数学家秦九韶(1202-1261)在1247年首次提出。秦九韶算法 五、数值运算中的一些原则 1、要有数值稳定性 (即能控制舍入误差的传播)例4 在四位十进制的限制下计算积分算法A: 算法B: 2、合理安排量级相差悬殊数间的运算次序,防止 “大数”吃掉“小数”;例5 设有在四位十进制的限制下计算其和 算法A: 从左往右算 ………….....算法B:从右往左算。………….....3、避免两个相近的数相减例6 求二次方程 算法A:利用公式的根 具有1位有效数字 3、避免两个相近的数相减例6 求二次方程 算法A:利用公式的根 具有1位有效数字 算法B:具有3位有效数字 3、避免两个相近的数相减例6 求二次方程 算法A:利用公式的根 具有1位有效数字 算法B:具有3位有效数字 算法C:3、避免两个相近的数相减一元二次方程的计算公式:阅读:
避免两个相近的数相减的常用方法:
参看任玉杰教材19-21页阅读:
避免两个相近的数相减的常用方法:
参看任玉杰教材19-21页(1)倒数变换法:(2)对数变换法:(3)余弦变换法:(4)泰勒级数法:4、避免接近于0的数作除数,防止溢出。5、简化计算步骤,减少运算次数。4、避免接近于0的数作除数,防止溢出。5、简化计算步骤,减少运算次数。 END 五、数值运算中的一些原则 1、要有数值稳定性 (即能控制舍入误差的传播)2、合理安排量级相差悬殊数间的运算次序,防止 “大数”吃掉“小数”;3、避免两个相近的数相减作业5:任玉杰习题1.2、1.3、1.4
同课章节目录
