北师大版九年级数学下册培优练习:1.1 锐角三角函数(附答案)
文档属性
| 名称 | 北师大版九年级数学下册培优练习:1.1 锐角三角函数(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 981.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-22 10:29:46 | ||
图片预览




文档简介
1.1 锐角三角函数
一、选择题(共13小题)
1. 如果 ,那么锐角 的度数是
A. B. C. D.
2. 如图,梯子(长度不变)跟地面所成的锐角为 ,关于 的三角函数值与梯子的倾斜程度之间的关系,叙述正确的是
A. 的值越大,梯子越陡 B. 的值越大,梯子越陡
C. 的值越小,梯子越陡 D. 陡缓程度与 的函数值无关
3. 如图,在由边长为 的小正方形组成的网格中,点 ,, 都在小正方形的顶点上,则 的值为
A. B. C. D.
4. 如果 中,,,则下列最确切的结论是
A. 是直角三角形 B. 是等腰三角形
C. 是等腰直角三角形 D. 是锐角三角形
5. 在 中,,,,则 的值是
A. B. C. D.
6. 如图,在 中,, 于 ,,,设 ,那么 的值是
A. B. C. D.
7. 将一张矩形纸片 (如图)那样折起,使顶点 落在 处,测量得 ,.则 为
A. B. C. D.
8. 已知 中,,若 ,,则 的值是
A. B. C. D.
9. 如果 是锐角,且 ,那么 的值为
A. B. C. D.
10. 如果把一个锐角 的三边的长都扩大为原来的 倍,那么锐角 的余切值
A. 扩大为原来的 倍 B. 缩小为原来的
C. 没有变化 D. 不能确定
11. 如图是由边长相同的小正方形组成的网格,,,, 四点均在正方形网格的格点上,线段 , 相交于点 ,则图中 的正切值是
A. B. C. D.
12. 如图,在网格中,小正方形的边长均为 ,点 ,, 都在格点上,则 的正切值是
A. B. C. D.
13. 如图,在 的正方形方格图形中,小正方形的顶点称为格点, 的顶点都在格点上,则图中 的余弦值是
A. B. C. D.
二、填空题(共6小题)
14. 如图, 的顶点都是正方形网格中的格点,则 ?.
15. 如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧 与墙 平行且距离为 米,一辆小汽车车门宽 为 米,当车门打开角度 为 时,车门是否会碰到墙? ?;(填“是”或“否”)请简述你的理由 ?.
(参考数据:,,)
16. 已知当 时,恒有 成立,则实数 的取值范围是 ?.
17. 如图,正方形 的边长为 ,过点 作 ,,连接 ,则 ?.
18. 在 中,若 ,,,则 ?.
19. 如图,若锐角 内接于 ,点 在 外(与点 在 同侧),则下列三个结论:;; 中,正确的结论为 .
三、解答题(共6小题)
20. 甲、乙两位同学在计算锐角 的正弦值时,甲的答案为 ,乙的答案为 ,请你不看他们的解答过程,迅速判断哪位同学的解答一定是错误的,并说明理由.
21. 如图,已知 和射线 上一点 (点 与点 不重合,且点 到 , 的距离分别为 ,).
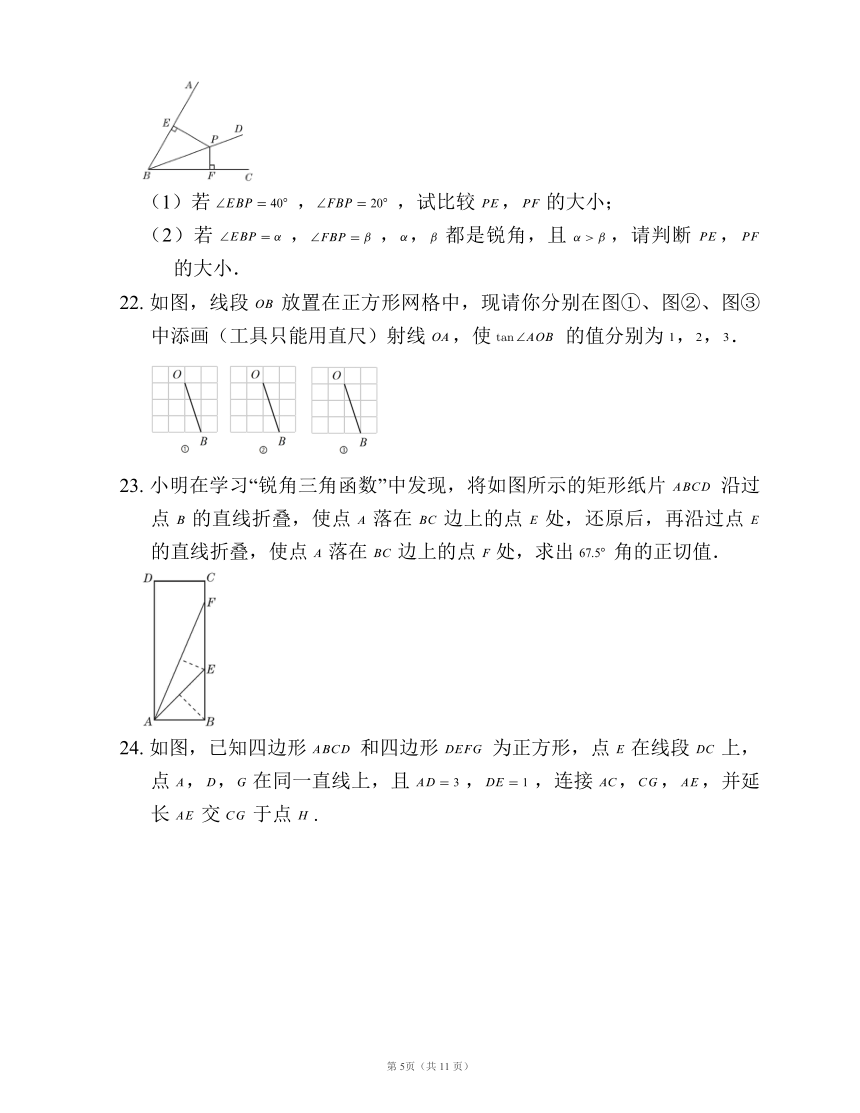
(1)若 ,,试比较 , 的大小;
(2)若 ,,, 都是锐角,且 ,请判断 , 的大小.
22. 如图,线段 放置在正方形网格中,现请你分别在图①、图②、图③中添画(工具只能用直尺)射线 ,使 的值分别为 ,,.
23. 小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片 沿过点 的直线折叠,使点 落在 边上的点 处,还原后,再沿过点 的直线折叠,使点 落在 边上的点 处,求出 角的正切值.
24. 如图,已知四边形 和四边形 为正方形,点 在线段 上,点 ,, 在同一直线上,且 ,,连接 ,,,并延长 交 于点 .
(1)求 的值.
(2)求线段 的长.
25. 若锐角 满足 ,求 的值;
答案
1. A
2. A
3. C
4. C
5. A
6. D
7. B
8. C
9. B
10. C
11. D 【解析】连接 ,,
由网格可得:,
又 ,
,
,
,,,
,
解得:,
.
12. D 【解析】如图,连接 .
由勾股定理,得 ,,,
所以 为直角三角形,且 ,
所以 .
13. D 【解析】 由图可知,,,,
是直角三角形,且 ,
.
14.
15. 否,求出点 与直线 的距离 ,通过计算可得 ,所以车门不会碰到墙
16.
17.
【解析】延长 使 ,连接 ,过 点作 ,垂足为 .
根据题干条件证明 ,得出 ,然后在 中,求出 的值,进而求出 的值.
18.
19.
【解析】设 交 于点 ,连接 .
因为 ,,
所以 ,
所以 ;;,
所以正确的结论有:.
20. 乙的答案一定是错误的,因为 ,
由于 的对边一定小于斜边,
所以 一定小于 .
21. (1) ,,
,.
又 ,
.
.
??????(2) , 都是锐角,且 ,
.
又 ,,
.
.
22. 如图①所示,
;
如图②所示,
;
如图③所示,
.
23. 将矩形纸片 沿过点 的直线折叠,使点 落在 边上的点 处,
,,
还原后,再沿过点 的直线折叠,使点 落在 边上的点 处,
,,
.
设 ,则 ,
.
24. (1) 由题意知 ,.
过 点做 于点 ,
所以 ,易知 ,所以 是等腰直角三角形,
所以 ,
所以 .
??????(2) 在 与 中,
所以 ,所以 ,
又因为 ,
所以 ,
所以 ,
因为 ,
所以 ,
所以 .
25. ∵ , ,
∴ .
一、选择题(共13小题)
1. 如果 ,那么锐角 的度数是
A. B. C. D.
2. 如图,梯子(长度不变)跟地面所成的锐角为 ,关于 的三角函数值与梯子的倾斜程度之间的关系,叙述正确的是
A. 的值越大,梯子越陡 B. 的值越大,梯子越陡
C. 的值越小,梯子越陡 D. 陡缓程度与 的函数值无关
3. 如图,在由边长为 的小正方形组成的网格中,点 ,, 都在小正方形的顶点上,则 的值为
A. B. C. D.
4. 如果 中,,,则下列最确切的结论是
A. 是直角三角形 B. 是等腰三角形
C. 是等腰直角三角形 D. 是锐角三角形
5. 在 中,,,,则 的值是
A. B. C. D.
6. 如图,在 中,, 于 ,,,设 ,那么 的值是
A. B. C. D.
7. 将一张矩形纸片 (如图)那样折起,使顶点 落在 处,测量得 ,.则 为
A. B. C. D.
8. 已知 中,,若 ,,则 的值是
A. B. C. D.
9. 如果 是锐角,且 ,那么 的值为
A. B. C. D.
10. 如果把一个锐角 的三边的长都扩大为原来的 倍,那么锐角 的余切值
A. 扩大为原来的 倍 B. 缩小为原来的
C. 没有变化 D. 不能确定
11. 如图是由边长相同的小正方形组成的网格,,,, 四点均在正方形网格的格点上,线段 , 相交于点 ,则图中 的正切值是
A. B. C. D.
12. 如图,在网格中,小正方形的边长均为 ,点 ,, 都在格点上,则 的正切值是
A. B. C. D.
13. 如图,在 的正方形方格图形中,小正方形的顶点称为格点, 的顶点都在格点上,则图中 的余弦值是
A. B. C. D.
二、填空题(共6小题)
14. 如图, 的顶点都是正方形网格中的格点,则 ?.
15. 如图,是一辆小汽车与墙平行停放的平面示意图,汽车靠墙一侧 与墙 平行且距离为 米,一辆小汽车车门宽 为 米,当车门打开角度 为 时,车门是否会碰到墙? ?;(填“是”或“否”)请简述你的理由 ?.
(参考数据:,,)
16. 已知当 时,恒有 成立,则实数 的取值范围是 ?.
17. 如图,正方形 的边长为 ,过点 作 ,,连接 ,则 ?.
18. 在 中,若 ,,,则 ?.
19. 如图,若锐角 内接于 ,点 在 外(与点 在 同侧),则下列三个结论:;; 中,正确的结论为 .
三、解答题(共6小题)
20. 甲、乙两位同学在计算锐角 的正弦值时,甲的答案为 ,乙的答案为 ,请你不看他们的解答过程,迅速判断哪位同学的解答一定是错误的,并说明理由.
21. 如图,已知 和射线 上一点 (点 与点 不重合,且点 到 , 的距离分别为 ,).
(1)若 ,,试比较 , 的大小;
(2)若 ,,, 都是锐角,且 ,请判断 , 的大小.
22. 如图,线段 放置在正方形网格中,现请你分别在图①、图②、图③中添画(工具只能用直尺)射线 ,使 的值分别为 ,,.
23. 小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片 沿过点 的直线折叠,使点 落在 边上的点 处,还原后,再沿过点 的直线折叠,使点 落在 边上的点 处,求出 角的正切值.
24. 如图,已知四边形 和四边形 为正方形,点 在线段 上,点 ,, 在同一直线上,且 ,,连接 ,,,并延长 交 于点 .
(1)求 的值.
(2)求线段 的长.
25. 若锐角 满足 ,求 的值;
答案
1. A
2. A
3. C
4. C
5. A
6. D
7. B
8. C
9. B
10. C
11. D 【解析】连接 ,,
由网格可得:,
又 ,
,
,
,,,
,
解得:,
.
12. D 【解析】如图,连接 .
由勾股定理,得 ,,,
所以 为直角三角形,且 ,
所以 .
13. D 【解析】 由图可知,,,,
是直角三角形,且 ,
.
14.
15. 否,求出点 与直线 的距离 ,通过计算可得 ,所以车门不会碰到墙
16.
17.
【解析】延长 使 ,连接 ,过 点作 ,垂足为 .
根据题干条件证明 ,得出 ,然后在 中,求出 的值,进而求出 的值.
18.
19.
【解析】设 交 于点 ,连接 .
因为 ,,
所以 ,
所以 ;;,
所以正确的结论有:.
20. 乙的答案一定是错误的,因为 ,
由于 的对边一定小于斜边,
所以 一定小于 .
21. (1) ,,
,.
又 ,
.
.
??????(2) , 都是锐角,且 ,
.
又 ,,
.
.
22. 如图①所示,
;
如图②所示,
;
如图③所示,
.
23. 将矩形纸片 沿过点 的直线折叠,使点 落在 边上的点 处,
,,
还原后,再沿过点 的直线折叠,使点 落在 边上的点 处,
,,
.
设 ,则 ,
.
24. (1) 由题意知 ,.
过 点做 于点 ,
所以 ,易知 ,所以 是等腰直角三角形,
所以 ,
所以 .
??????(2) 在 与 中,
所以 ,所以 ,
又因为 ,
所以 ,
所以 ,
因为 ,
所以 ,
所以 .
25. ∵ , ,
∴ .
