2018~2019学年上海市复兴中学高二下期末数学试卷(有答案)
文档属性
| 名称 | 2018~2019学年上海市复兴中学高二下期末数学试卷(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 767.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 00:00:00 | ||
图片预览


文档简介
M={0,1,2},函数y=f(x)的定义域为D={1234},值域
若A=M,求不同函数y=f(x)的个数
若满足f(1)+f(2)+f(3)+f(4)=4,求不同的函数y=f(x)的个数
E知/005a0的大值为正实数合Ax+1y
求A和B
2淀定义A和B的差集:4-B={xe且xgB,设a、b、x均为整数且x∈AP(E)
为x取自4一B的概率,P(D)为x取自4∩3的,写出a与b的二组值,使P(E=3
并化简:CC+C2C"+C2、C4=2+…+C-C
2)证
(C)+2(C2)2+…+n(C)2=nC2
21已知a∈R,函数f(x)
解不等式f(x
)-1og[(a-4)x+2a-5]=0的解集中怡好
值范围;
a>0,若对任意t
函数f(x)在区间[+t+]上的最大值与最小值的差不
超过
参考答案
填空题
7.-4B.126
二、选择题
解答题
17.(1)30
9.(1)A={a0),B={-bb)
)a=-4,b=2或
20.(1)C2-
2)证明略
2)(12]U34
2018学年复兴中学高二年级下学期期末卷
2019.6
1设集合A={-10,B={0,23,则(C1n∩B
>1的解集
对于
若a+b≤0,则a
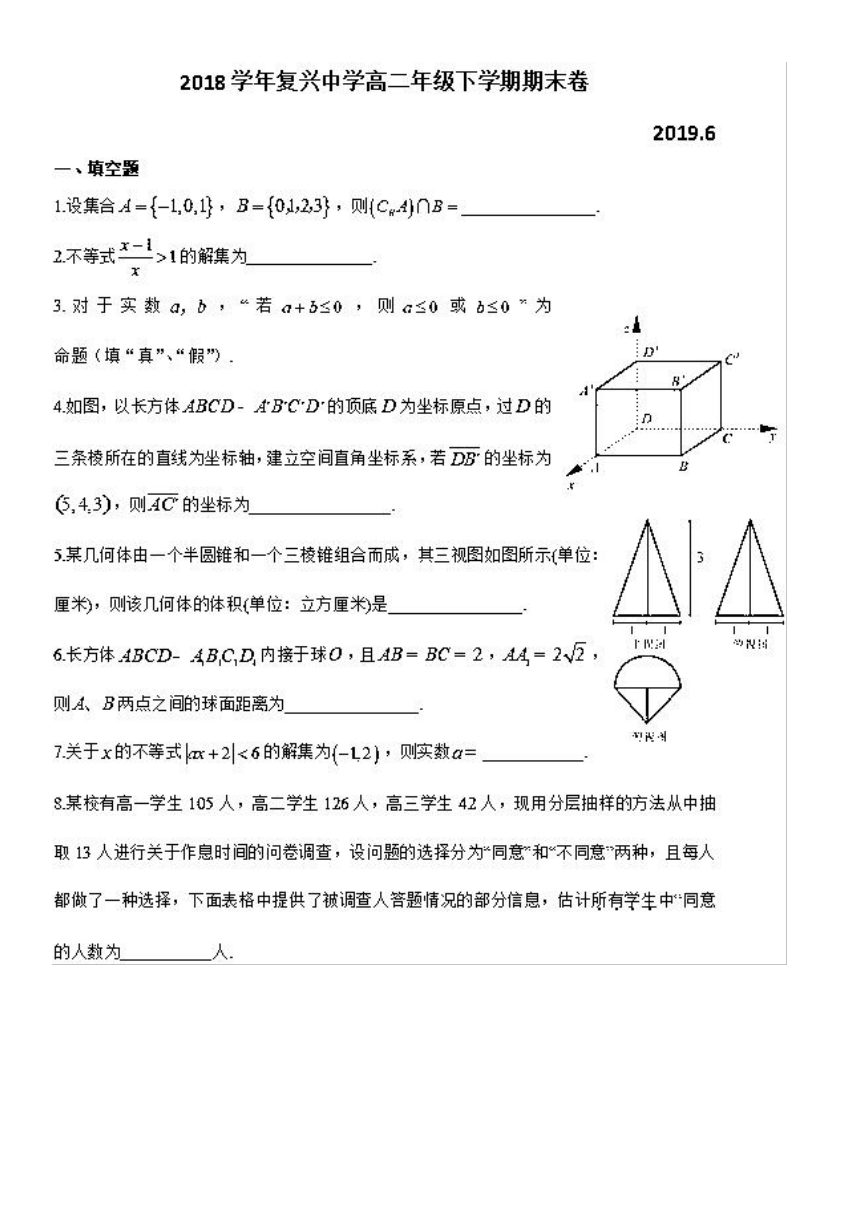
4如图,以长方体ABCD-ABCD的顶底D为坐标原点,过D的
条棱所在的直线为坐标轴,建立空间直角坐标系,若DB的坐标为
43),则C的坐标为
5某几何体由
四和一个三被组合而,耗如圈所位∧NA
厘米),则该几何体的体积单位:立方厘米是
6长方体BCD-ABCD内接于球O,且AB=BC=2,AA=22
则A、B两点之间的球面距离为
7关于x的不等式{a+21<6的解集为(-12},则实数
8某校有高一学生
二学生126人,高三学生42人,现用分层抽样的方法从中抽
取13人进行关于作息时间的问卷调查,设问题的选择分为同意和不同意两种,且每
情况的部分信息,估计所有学生中同意
同意
为
0从正方体六个面的对角线中任取两条作为一对,这对对角线所成的角为60的概率
1已知正实数x、y满足1+1=1,则4x+9的最小值
12定义工(4)为集合A中所有元素的乘积,规定:只有一个元素时,乘积即为该元素本身
已知集合M
34,集合M的所有非空子
为M,,M
I(M)+I(M2)
选择题
13若a、b为
A充要条件
B充分非必要条件
C必要非充分条件
D既非充分也非必要条件
14如图,在下列四个正方体中,A,B为正方体的两个顶点,M、MQ为所在棱的中点
在这四个正方体中,直接AB与平面MMO不平行的是
单包
15在一次数学测试中,高某班50名学生成绩的平均分为82,方差为82,则下列四个数
中不可能是该班数学成绩的是()
直三棱柱BC-ABC的底面为直角三角形,两直角边B和AC的长分别为4
和3,侧棱4A1的长为5
(1)求三棱柱ABC-ABC的体积
2)设M是BC中点,求直线AM与平面ABC所成角的大
同课章节目录
