高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.1.1平面(35张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.1.1平面(35张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 00:00:00 | ||
图片预览






文档简介
课件35张PPT。第二章 点、直线、平面之间的位置关系
2.1 空间点、直线、平面之间的位置关系
2.1.1 平 面课标要求:1.正确理解平面的概念.2.能用符号语言描述空间点、直线、平面之间的位置关系.3.能用图形、文字、符号三种语言描述三个公理,理解三个公理的地位与作用.自主学习知识探究1.平面
(1)平面的概念
几何里所说的“平面”,是从课桌面、黑板面、海面这样的一些物体中抽象出来的.几何里的平面是 的.
(2)平面的画法
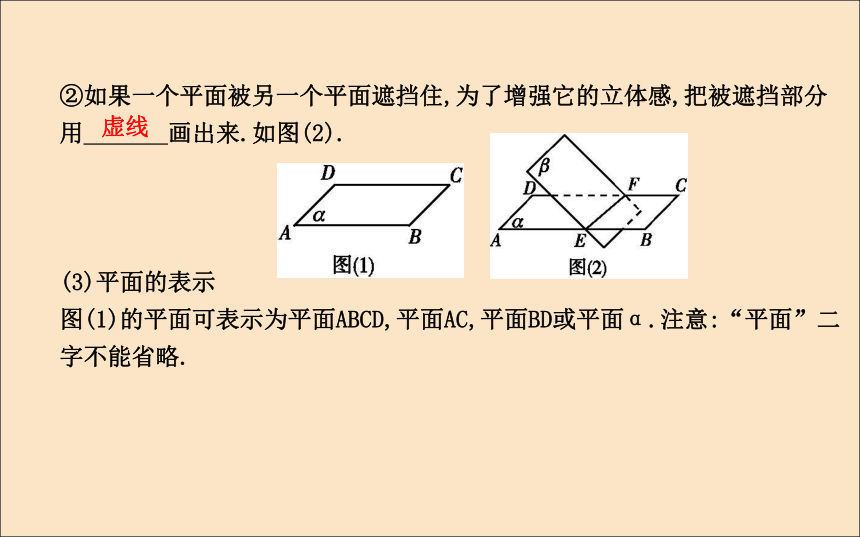
①水平放置的平面通常画成一个平行四边形,用平行四边形表示平面,平行四边形的锐角通常画成 ,且横边长等于其邻边长的 .如图(1).无限延展45° 2倍②如果一个平面被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用 画出来.如图(2).
(3)平面的表示
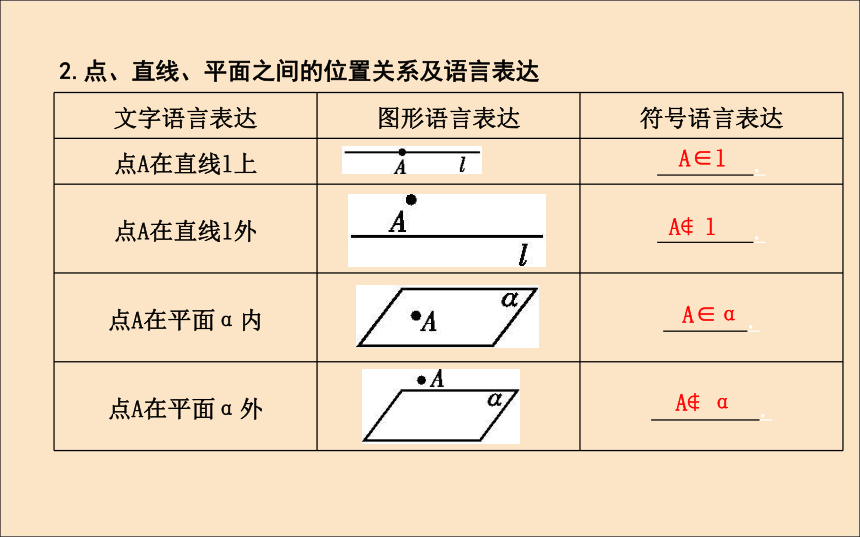
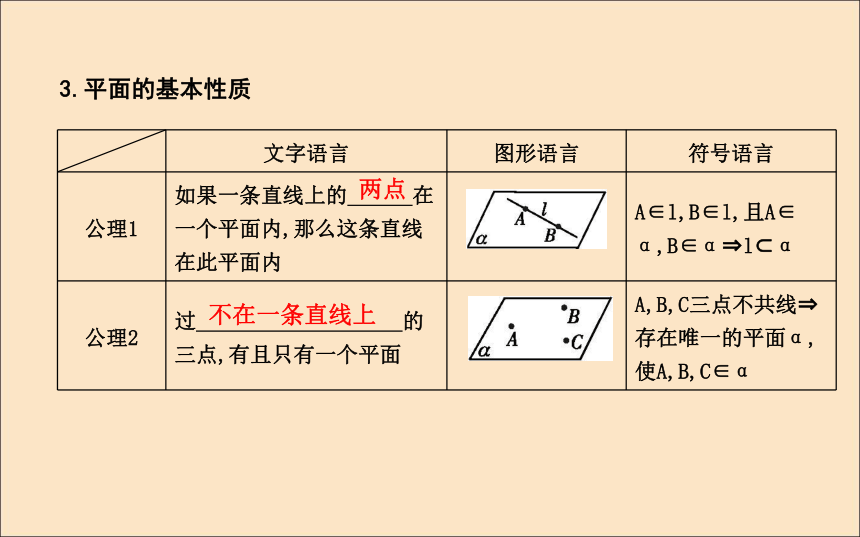
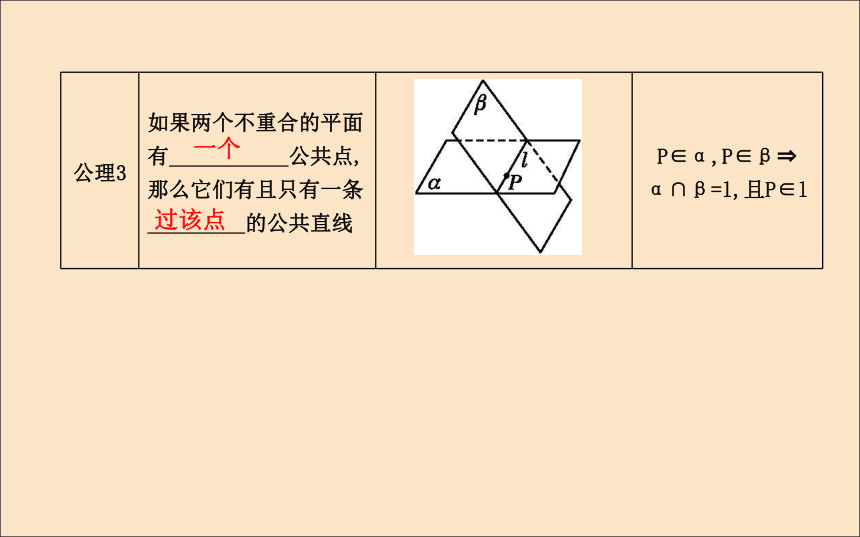
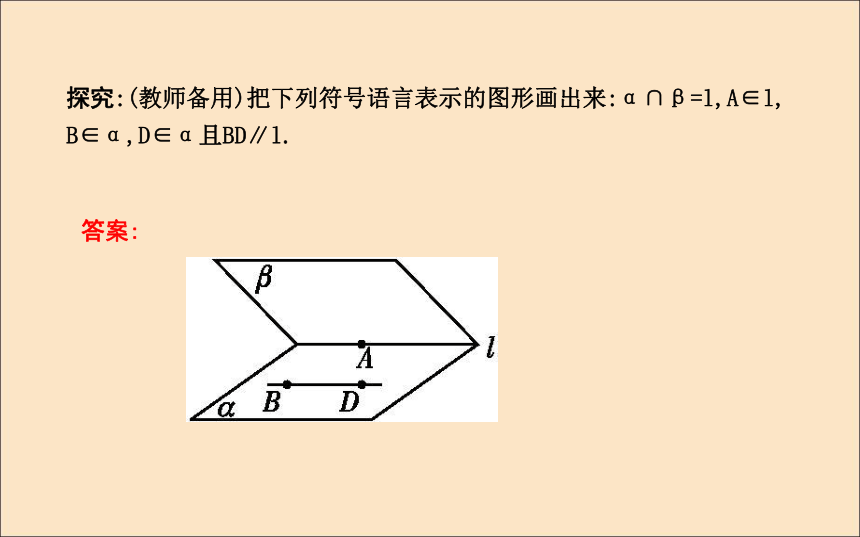
图(1)的平面可表示为平面ABCD,平面AC,平面BD或平面α.注意:“平面”二字不能省略.虚线2.点、直线、平面之间的位置关系及语言表达A∈lA?lA∈αA?αl?αl?αα∩β=l3.平面的基本性质两点不在一条直线上一个过该点 探究:(教师备用)把下列符号语言表示的图形画出来:α∩β=l,A∈l,
B∈α,D∈α且BD∥l.答案: 自我检测1.三条直线两两相交,可以确定平面的个数是( )
(A)1个 (B)1个或2个
(C)1个或3个 (D)3个
2.如图所示,用符号语言可表达为( )
(A)α∩β=m,n?α,m∩n=A
(B)α∩β=m,n∈α,m∩n=A
(C)α∩β=m,n?α,A?m,A?n
(D)α∩β=m,n∈α,A∈m,A∈nCA3.三个平面将空间最多能分成( )
(A)6部分 (B)7部分
(C)8部分 (D)9部分
4.如果直线a?平面α,直线b?平面α,M∈a,N∈b,M∈l,N∈l,则( )
(A)l?α
(B)l?α
(C)l∩α=M
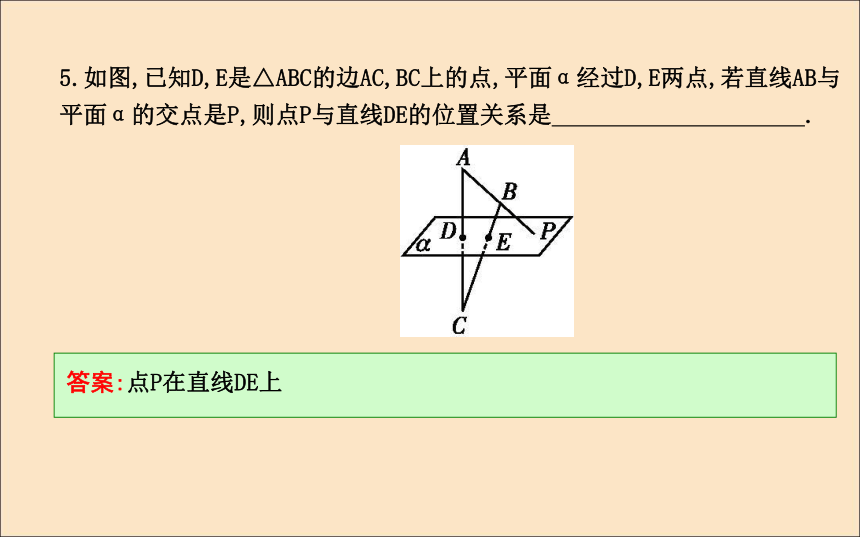
(D)l∩α=NCA解析:因为M∈l,N∈l,且M∈α,N∈α,所以l?α.5.如图,已知D,E是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB与平面α的交点是P,则点P与直线DE的位置关系是 .?答案:点P在直线DE上题型一文字语言、图形语言、符号语言的转换【例1】 完成下列各题:
(1)将下列文字语言转换为符号语言.
①点A在平面α内,但不在平面β内;
②直线a经过平面α外一点M;
③直线l在平面α内,又在平面β内(即平面α和平面β相交于直线l).课堂探究解:(1)①A∈α,A?β.②M∈a,M?α.③α∩β=l.(2)将下列符号语言转换为图形语言.
①a?α,b∩α=A,A?a;
②α∩β=c,a?α,b?β,a∥c,b∩c=P.方法技巧 实现三种语言转换要注意
(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
(2)符号语言的意义.如点与直线的位置关系只能用“∈”或“?”,直线与平面的位置关系只能用“?”或“?”.
(3)由符号语言或文字语言画相应的图形时,要注意把被遮挡的部分画成 虚线.即时训练1-1:(1)A,B,C表示不同的点,n,l表示不同的直线,α,β表示不同的平面,下列推理表述不正确的是( )
(A)A∈l,A∈α,B∈l,B∈α?l?α
(B)A∈α,A∈β,B∈β,B∈α?α∩β=直线AB
(C)A,B,C∈α,A,B,C∈β,且A,B,C不共线?α与β重合
(D)l∈α,n∈α,l∩n=A?l与n确定唯一平面
(2)如图,用符号表示下列图形中点、直线、平面之间的位置关系.解:(1)选D.(2)在①中,α∩β=l,a∩α=A,a∩β=B.在②中,α∩β=l,
a?α,b?β,a∩l=P,b∩l=P.1-2:根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:(1)A∈α,B?α;(2)l?α,m∩α=A,A?l;(3)P∈l,P?α,Q∈l,
Q∈α.解:(1)点A在平面α内,点B不在平面α内.
(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上.
(3)直线l经过平面α外一点P和平面α内一点Q.
图形分别如图(1),(2),(3)所示.题型二点线共面【例2-1】 如图,l1∩l2=A,l2∩l3=B,l1∩l3=C,求证直线l1,l2,l3在同一平面内.证明:法一 (纳入法)
因为l1∩l2=A,所以l1和l2在同一平面α内.
因为l2∩l3=B,所以B∈l2.
又因为l2?α,所以B∈α.同理可证C∈α.
又因为B∈l3,C∈l3,所以l3?α.
所以直线l1,l2,l3在同一平面内.法二 (重合法)
因为l1∩l2=A,所以l1,l2确定一个平面α.
因为l2∩l3=B,所以l2,l3确定一个平面β.
因为A∈l2,l2?α,所以A∈α.
因为A∈l2,l2?β,所以A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.
所以不共线的三个点A,B,C既在平面α内,又在平面β内.
所以平面α和β重合,即直线l1,l2,l3在同一平面内.【2-2】 如图,点A,B∈平面β,直线a?平面α,点M?a,M∈α,α∩β=l,试在直线a上找一点N,使MN与AB相交.解:在平面β内作直线AB交l于点P,连接MP,则MP与a的交点即是点N.方法技巧 证明点线共面问题的理论依据是公理2,常用方法有:
(1)纳入法:先由部分直线确定一个平面,再证明其他直线在这个平面内.
(2)重合法:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合.即时训练2-1:空间两两相交且共点的三条直线,可以确定的平面数是( )
(A)1 (B)2
(C)3 (D)1或3解析:两两相交且共点的三条直线若在一个平面内,可确定一个平面,若不在一平面内,每两条直线可确定一个平面,共可确定3个平面,故选D.2-2:已知在正方体ABCD-A1B1C1D1中.
(1)AA1与CC1是否在同一平面内?解:(1)如图所示,在正方体ABCD-A1B1C1D1中,
因为AA1∥CC1,所以AA1与CC1可确定平面ACC1A1,
所以AA1与CC1在同一平面内.(2)点B,C1,D是否在同一平面内?
(3)画出平面ACC1A1与平面BC1D的交线,平面ACD1与平面BDC1的交线.解:(2)因为点B,C1,D不共线,
所以B,C1,D可确定平面BC1D,
所以点B,C1,D在同一平面内.
(3)因为AC∩BD=O,D1C∩DC1=E,
所以O∈平面ACC1A1,且O∈平面BC1D.
又C1∈平面ACC1A1,且C1∈平面BC1D,
所以平面ACC1A1∩平面BC1D=OC1.
同理平面ACD1∩平面BDC1=OE.题型三多点共线、多线共点问题【例3-1】 (12分)如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE,D1F,DA三线交于一点.变式探究:若将题目条件中的“E,F分别为AB,AA1的中点”改成E,F分别为AB,
AA1上的点,且D1F∩CE=M,求证:M∈AD.证明:因为D1F∩CE=M,
且D1F?平面A1D1DA,
所以M∈平面A1D1DA,
同理M∈平面BCDA,
从而M在两个平面的交线上,
因为平面A1D1DA∩平面BCDA=AD,
所以M∈AD成立.方法技巧 (1)证明三线共点常用的方法:
先证明两条直线相交于一点,然后证明这个点在两个平面内,第三条线是这两个平面的交线,于是该点在第三条直线上,从而得到三线共点.也可以先证明a,b相交于一点A,b与c相交于一点B,再证明A,B是同一点,从而得到a,b,c三线共点.
(2)类比线共点的证明方法,可得到三点共线的证明方法:
①首先找出两个平面的交线,然后证明这三点都是这两个平面的公共点,根据公理3,可推知这些点都在交线上,即三点共线.
②选择其中两点确定一条直线,然后证明第三个点也在这条直线上.【3-2】 如图所示,在长方体ABCD-A1B1C1D1中,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确的是( )
(A)A,M,O三点共线
(B)A,M,O,A1不共面
(C)A,M,C,O不共面
(D)B,B1,O,M共面解析:连接A1C1,AC,则A1C1∥AC.
所以A1,C1,C,A四点共面.
所以A1C?平面ACC1A1.
因为M∈A1C,所以M∈平面ACC1A1,又M∈平面AB1D1,
所以M在平面ACC1A1与平面AB1D1的交线上,
同理O也在平面ACC1A1与平面AB1D1的交线上,
所以A,M,O三点共线.故选A.即时训练3-1:如图,△ABC在平面α外,AB∩α=P,AC∩α=Q,BC∩α=R.求证:P,Q,R三点共线.解:因为AB∩α=P,
所以P∈AB,P∈α.
又AB?平面ABC,所以P∈平面ABC.
由公理3可知点P在平面ABC与平面α的交线上,
同理可证Q,R也在平面ABC与平面α的交线上,
所以P,Q,R三点共线.
2.1 空间点、直线、平面之间的位置关系
2.1.1 平 面课标要求:1.正确理解平面的概念.2.能用符号语言描述空间点、直线、平面之间的位置关系.3.能用图形、文字、符号三种语言描述三个公理,理解三个公理的地位与作用.自主学习知识探究1.平面
(1)平面的概念
几何里所说的“平面”,是从课桌面、黑板面、海面这样的一些物体中抽象出来的.几何里的平面是 的.
(2)平面的画法
①水平放置的平面通常画成一个平行四边形,用平行四边形表示平面,平行四边形的锐角通常画成 ,且横边长等于其邻边长的 .如图(1).无限延展45° 2倍②如果一个平面被另一个平面遮挡住,为了增强它的立体感,把被遮挡部分用 画出来.如图(2).
(3)平面的表示
图(1)的平面可表示为平面ABCD,平面AC,平面BD或平面α.注意:“平面”二字不能省略.虚线2.点、直线、平面之间的位置关系及语言表达A∈lA?lA∈αA?αl?αl?αα∩β=l3.平面的基本性质两点不在一条直线上一个过该点 探究:(教师备用)把下列符号语言表示的图形画出来:α∩β=l,A∈l,
B∈α,D∈α且BD∥l.答案: 自我检测1.三条直线两两相交,可以确定平面的个数是( )
(A)1个 (B)1个或2个
(C)1个或3个 (D)3个
2.如图所示,用符号语言可表达为( )
(A)α∩β=m,n?α,m∩n=A
(B)α∩β=m,n∈α,m∩n=A
(C)α∩β=m,n?α,A?m,A?n
(D)α∩β=m,n∈α,A∈m,A∈nCA3.三个平面将空间最多能分成( )
(A)6部分 (B)7部分
(C)8部分 (D)9部分
4.如果直线a?平面α,直线b?平面α,M∈a,N∈b,M∈l,N∈l,则( )
(A)l?α
(B)l?α
(C)l∩α=M
(D)l∩α=NCA解析:因为M∈l,N∈l,且M∈α,N∈α,所以l?α.5.如图,已知D,E是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB与平面α的交点是P,则点P与直线DE的位置关系是 .?答案:点P在直线DE上题型一文字语言、图形语言、符号语言的转换【例1】 完成下列各题:
(1)将下列文字语言转换为符号语言.
①点A在平面α内,但不在平面β内;
②直线a经过平面α外一点M;
③直线l在平面α内,又在平面β内(即平面α和平面β相交于直线l).课堂探究解:(1)①A∈α,A?β.②M∈a,M?α.③α∩β=l.(2)将下列符号语言转换为图形语言.
①a?α,b∩α=A,A?a;
②α∩β=c,a?α,b?β,a∥c,b∩c=P.方法技巧 实现三种语言转换要注意
(1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.
(2)符号语言的意义.如点与直线的位置关系只能用“∈”或“?”,直线与平面的位置关系只能用“?”或“?”.
(3)由符号语言或文字语言画相应的图形时,要注意把被遮挡的部分画成 虚线.即时训练1-1:(1)A,B,C表示不同的点,n,l表示不同的直线,α,β表示不同的平面,下列推理表述不正确的是( )
(A)A∈l,A∈α,B∈l,B∈α?l?α
(B)A∈α,A∈β,B∈β,B∈α?α∩β=直线AB
(C)A,B,C∈α,A,B,C∈β,且A,B,C不共线?α与β重合
(D)l∈α,n∈α,l∩n=A?l与n确定唯一平面
(2)如图,用符号表示下列图形中点、直线、平面之间的位置关系.解:(1)选D.(2)在①中,α∩β=l,a∩α=A,a∩β=B.在②中,α∩β=l,
a?α,b?β,a∩l=P,b∩l=P.1-2:根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:(1)A∈α,B?α;(2)l?α,m∩α=A,A?l;(3)P∈l,P?α,Q∈l,
Q∈α.解:(1)点A在平面α内,点B不在平面α内.
(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上.
(3)直线l经过平面α外一点P和平面α内一点Q.
图形分别如图(1),(2),(3)所示.题型二点线共面【例2-1】 如图,l1∩l2=A,l2∩l3=B,l1∩l3=C,求证直线l1,l2,l3在同一平面内.证明:法一 (纳入法)
因为l1∩l2=A,所以l1和l2在同一平面α内.
因为l2∩l3=B,所以B∈l2.
又因为l2?α,所以B∈α.同理可证C∈α.
又因为B∈l3,C∈l3,所以l3?α.
所以直线l1,l2,l3在同一平面内.法二 (重合法)
因为l1∩l2=A,所以l1,l2确定一个平面α.
因为l2∩l3=B,所以l2,l3确定一个平面β.
因为A∈l2,l2?α,所以A∈α.
因为A∈l2,l2?β,所以A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.
所以不共线的三个点A,B,C既在平面α内,又在平面β内.
所以平面α和β重合,即直线l1,l2,l3在同一平面内.【2-2】 如图,点A,B∈平面β,直线a?平面α,点M?a,M∈α,α∩β=l,试在直线a上找一点N,使MN与AB相交.解:在平面β内作直线AB交l于点P,连接MP,则MP与a的交点即是点N.方法技巧 证明点线共面问题的理论依据是公理2,常用方法有:
(1)纳入法:先由部分直线确定一个平面,再证明其他直线在这个平面内.
(2)重合法:先说明一些直线在一个平面内,另一些直线在另一个平面内,再证明两个平面重合.即时训练2-1:空间两两相交且共点的三条直线,可以确定的平面数是( )
(A)1 (B)2
(C)3 (D)1或3解析:两两相交且共点的三条直线若在一个平面内,可确定一个平面,若不在一平面内,每两条直线可确定一个平面,共可确定3个平面,故选D.2-2:已知在正方体ABCD-A1B1C1D1中.
(1)AA1与CC1是否在同一平面内?解:(1)如图所示,在正方体ABCD-A1B1C1D1中,
因为AA1∥CC1,所以AA1与CC1可确定平面ACC1A1,
所以AA1与CC1在同一平面内.(2)点B,C1,D是否在同一平面内?
(3)画出平面ACC1A1与平面BC1D的交线,平面ACD1与平面BDC1的交线.解:(2)因为点B,C1,D不共线,
所以B,C1,D可确定平面BC1D,
所以点B,C1,D在同一平面内.
(3)因为AC∩BD=O,D1C∩DC1=E,
所以O∈平面ACC1A1,且O∈平面BC1D.
又C1∈平面ACC1A1,且C1∈平面BC1D,
所以平面ACC1A1∩平面BC1D=OC1.
同理平面ACD1∩平面BDC1=OE.题型三多点共线、多线共点问题【例3-1】 (12分)如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE,D1F,DA三线交于一点.变式探究:若将题目条件中的“E,F分别为AB,AA1的中点”改成E,F分别为AB,
AA1上的点,且D1F∩CE=M,求证:M∈AD.证明:因为D1F∩CE=M,
且D1F?平面A1D1DA,
所以M∈平面A1D1DA,
同理M∈平面BCDA,
从而M在两个平面的交线上,
因为平面A1D1DA∩平面BCDA=AD,
所以M∈AD成立.方法技巧 (1)证明三线共点常用的方法:
先证明两条直线相交于一点,然后证明这个点在两个平面内,第三条线是这两个平面的交线,于是该点在第三条直线上,从而得到三线共点.也可以先证明a,b相交于一点A,b与c相交于一点B,再证明A,B是同一点,从而得到a,b,c三线共点.
(2)类比线共点的证明方法,可得到三点共线的证明方法:
①首先找出两个平面的交线,然后证明这三点都是这两个平面的公共点,根据公理3,可推知这些点都在交线上,即三点共线.
②选择其中两点确定一条直线,然后证明第三个点也在这条直线上.【3-2】 如图所示,在长方体ABCD-A1B1C1D1中,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确的是( )
(A)A,M,O三点共线
(B)A,M,O,A1不共面
(C)A,M,C,O不共面
(D)B,B1,O,M共面解析:连接A1C1,AC,则A1C1∥AC.
所以A1,C1,C,A四点共面.
所以A1C?平面ACC1A1.
因为M∈A1C,所以M∈平面ACC1A1,又M∈平面AB1D1,
所以M在平面ACC1A1与平面AB1D1的交线上,
同理O也在平面ACC1A1与平面AB1D1的交线上,
所以A,M,O三点共线.故选A.即时训练3-1:如图,△ABC在平面α外,AB∩α=P,AC∩α=Q,BC∩α=R.求证:P,Q,R三点共线.解:因为AB∩α=P,
所以P∈AB,P∈α.
又AB?平面ABC,所以P∈平面ABC.
由公理3可知点P在平面ABC与平面α的交线上,
同理可证Q,R也在平面ABC与平面α的交线上,
所以P,Q,R三点共线.
