高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.1.2空间中直线与直线之间的位置关系(35张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.1.2空间中直线与直线之间的位置关系(35张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 16:46:46 | ||
图片预览










文档简介
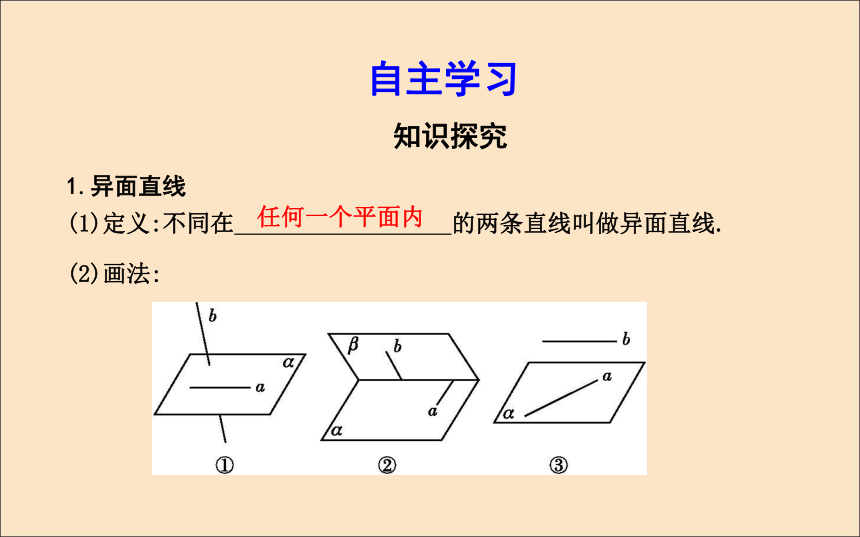
课件35张PPT。2.1.2 空间中直线与直线之间的位置关系课标要求:1.会判断空间两直线的位置关系.2.理解两异面直线的定义,会求两异面直线所成的角.3.能用公理4和等角定理解决一些简单的相关问题.自主学习知识探究1.异面直线
(1)定义:不同在 的两条直线叫做异面直线.任何一个平面内(2)画法:2.空间两条直线的位置关系有且只有一个公共点探究1:(教师备用)若直线a?α,b?β,a和b一定异面吗?
答案:不一定.当a与b不同在任何一个平面内,a,b才异面.3.平行线的传递性
公理4:平行于同一条直线的两条直线 .
符号表示:a∥b,b∥c?a∥c.互相平行4.定理
空间中如果两个角的两边分别对应平行,那么这两个角 .
5.异面直线所成的角
(1)定义:已知两条异面直线a,b,经过空间任一点O作直线a′∥a,b′∥b,则a′与b′所成的 (或 )叫做异面直线a与b所成的角(或夹角).
(2)异面直线所成的角θ的取值范围:0°<θ≤90°.
(3)如果两条异面直线a,b所成的角是直角,就说这两条直线互相垂直,记作a⊥b.
探究2:(教师备用)若两条直线都与第三条直线垂直,这两条直线一定平 行吗?
答案:不一定.例如墙角处的三条直线两两垂直,但是没有任何两条直线是互相平行的.相等或互补锐角直角自我检测1.若a和b是异面直线,b和c是异面直线,则a和c的位置关系是( )
(A)异面或平行
(B)异面或相交
(C)异面
(D)相交、平行或异面D解析:借助长方体模型进行判断选D.2.若∠AOB=∠A1O1B1,且OA∥O1A1,OA与O1A1的方向相同,则下列结论中正确的是( )
(A)OB∥O1B1且方向相同 (B)OB∥O1B1
(C)OB与O1B1不平行 (D)OB与O1B1不一定平行
3.下列四个结论中假命题的个数是( )
①垂直于同一直线的两条直线互相平行;
②平行于同一直线的两直线平行;
③若直线a,b,c满足a∥b,b⊥c,则a⊥c;
④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线.
(A)1 (B)2
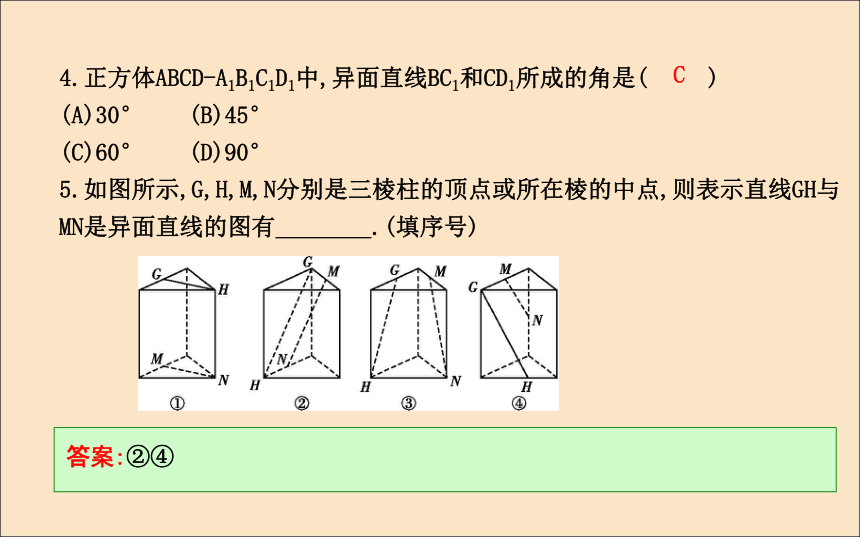
(C)3 (D)4DB4.正方体ABCD-A1B1C1D1中,异面直线BC1和CD1所成的角是( )
(A)30° (B)45°
(C)60° (D)90°
5.如图所示,G,H,M,N分别是三棱柱的顶点或所在棱的中点,则表示直线GH与MN是异面直线的图有 .(填序号)?答案:②④C题型一 空间位置关系的判断【例1-1】 已知空间四边形ABCD,AB≠AC,AE是△ABC中BC边上的高,DF是△BCD中BC边上的中线,求证:AE和DF是异面直线.课堂探究解:假设AE和DF不是异面直线,则AE和DF共面,设过AE,DF的平面为β,若E,F重合,则E为BC的中点,所以AB=AC,与AB≠AC相矛盾.若E,F不重合,因为B∈EF,C∈EF,而EF?β,所以B∈β,C∈β,又A∈β,D∈β,所以A,B,C,D四点共面,这与题设ABCD为空间四边形矛盾,综上可知,假设不成立,所以AE与DF为异面直线.【1-2】 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AA1,AB的中点,试判断下列各对线段所在直线的位置关系:(1)AB与CC1;(2)A1B1与DC;(3)A1C与D1B;(4)DC与BD1;(5)D1E与CF.解:(1)因为C∈平面ABCD,AB?平面ABCD,
又C?AB,C1?平面ABCD,所以AB与CC1异面.
(2)因为A1B1∥AB,AB∥DC,所以A1B1∥DC.
(3)因为A1D1∥B1C1,B1C1∥BC,
所以A1D1∥BC,
则A1,B,C,D1在同一平面内.
所以A1C与D1B相交.
(4)因为B∈平面ABCD,DC?平面ABCD,
又B?DC,D1?平面ABCD,所以DC与BD1异面.(5)CF与DA的延长线交于G,连接D1G,
因为AF∥DC,F为AB的中点,所以A为DG的中点.
又AE∥DD1,所以GD1过AA1的中点.
所以直线D1E与CF相交.方法技巧 判定两直线异面的常用方法
(1)定义法:由定义判断两直线不可能在同一平面内;
(2)排除法(反证法):排除两直线共面(平行或相交)的情况.即时训练1-1:正方体ABCD-A1B1C1D1中,与棱AB异面且垂直的棱有( )
(A)8条 (B)6条
(C)4条 (D)3条解析:如图所示,一共有12条棱,其中有三条与AB平行,有四条与AB相交,还剩四条,这四条是CC1,DD1,A1D1,B1C1都是与AB异面且垂直.故选C.题型二公理4及等角定理的应用【例2】 如图所示,在正方体ABCD-A′B′C′D′中,E,F,E′,F′分别是AB,BC,A′B′,B′C′的中点,求证:EE′∥FF′.证明:因为E,E′分别是AB,A′B′的中点,
所以BE∥B′E′,且BE=B′E′,
所以四边形EBB′E′是平行四边形.
所以EE′∥BB′,
同理可证FF′∥BB′,
所以EE′∥FF′.变式探究1:在本例中,若M,N分别是A′D′,C′D′的中点,求证:四边形ACNM是梯形.变式探究2:将本例变为已知E,E′分别是正方体ABCD-A′B′C′D′的棱AD,A′D′的中点,求证:∠BEC=∠B′E′C′.证明:如图所示,连接EE′.
因为E,E′分别是AD,A′D′的中点,
所以AE∥A′E′,且AE=A′E′.
所以四边形AEE′A′是平行四边形.
所以AA′∥EE′,且AA′=EE′.
又因为AA′∥BB′,且AA′=BB′,
所以EE′∥BB′,且EE′=BB′.
所以四边形BEE′B′是平行四边形.所以BE∥B′E′.
同理可证CE∥C′E′.
又∠BEC与∠B′E′C′的两边方向相同,
所以∠BEC=∠B′E′C′.方法技巧 证明两直线平行的常用方法:(1)利用平面几何的结论,如平行四边形的对边,三角形的中位线与底边;(2)定义法:即证明两条直线在同一个平面内且两直线没有公共点;(3)利用公理4:找到一条直线,使所证的直线都与这条直线平行.答案:平行2-2:在正方体ABCD-A1B1C1D1中,E,F分别为AD,AB的中点,M,N分别为B1C1,C1D1的中点.
求证:(1)MC∥A1E,A1F∥CN;(2)∠EA1F=∠NCM.证明:(2)由(1)知A1F∥CN,
MC∥A1E,
又A1E,A1F与CM,CN的方向分别相反,
所以∠EA1F=∠NCM.题型三求异面直线所成的角【例3-1】 在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,B1C1的中点,求异面直线DB1与EF所成角的大小.解:如图所示,连接A1C1,B1D1,并设它们相交于点O,取DD1的中点G,连接OG,A1G,C1G,
则OG∥B1D,EF∥A1C1,
所以∠GOA1为异面直线DB1与EF所成的角(或其补角).
因为GA1=GC1,O为A1C1的中点,
所以GO⊥A1C1.
所以异面直线DB1与EF所成的角为90°.方法技巧 求异面直线所成角的一般步骤:(1)找(或作出)异面直线所成的角——用平移法,若题设中有中点,常考虑中位线.(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的角.(3)结论——设(2)所求角大小为θ.若0°<θ≤90°,则θ即为所求;若90°<θ<180°,则180°-θ即为所求.即时训练3-1:(1)在正方体ABCD-A1B1C1D1中,CC1与BD1所成角的正弦值为 ;?(2)在正方体ABCD-A1B1C1D1中与侧面的对角线AD1成60°角的面对角线有
条.?解析:(2)因为ABCD-A1B1C1D1为正方体,
所以△AD1B1,△AD1C均为等边三角形.
所以AD1与BD,AD1与DC1,AD1与A1B,AD1与DC1,AD1与D1B1,AD1与AB1,AD1与AC,AD1与D1C均成60°角,共8条.
答案:(2)8于是∠EMH=60°,
则∠EMF=2∠EMH=120°.
所以异面直线AD,BC所成的角为∠EMF的补角,即异面直线AD,BC所成的角为60°.
(1)定义:不同在 的两条直线叫做异面直线.任何一个平面内(2)画法:2.空间两条直线的位置关系有且只有一个公共点探究1:(教师备用)若直线a?α,b?β,a和b一定异面吗?
答案:不一定.当a与b不同在任何一个平面内,a,b才异面.3.平行线的传递性
公理4:平行于同一条直线的两条直线 .
符号表示:a∥b,b∥c?a∥c.互相平行4.定理
空间中如果两个角的两边分别对应平行,那么这两个角 .
5.异面直线所成的角
(1)定义:已知两条异面直线a,b,经过空间任一点O作直线a′∥a,b′∥b,则a′与b′所成的 (或 )叫做异面直线a与b所成的角(或夹角).
(2)异面直线所成的角θ的取值范围:0°<θ≤90°.
(3)如果两条异面直线a,b所成的角是直角,就说这两条直线互相垂直,记作a⊥b.
探究2:(教师备用)若两条直线都与第三条直线垂直,这两条直线一定平 行吗?
答案:不一定.例如墙角处的三条直线两两垂直,但是没有任何两条直线是互相平行的.相等或互补锐角直角自我检测1.若a和b是异面直线,b和c是异面直线,则a和c的位置关系是( )
(A)异面或平行
(B)异面或相交
(C)异面
(D)相交、平行或异面D解析:借助长方体模型进行判断选D.2.若∠AOB=∠A1O1B1,且OA∥O1A1,OA与O1A1的方向相同,则下列结论中正确的是( )
(A)OB∥O1B1且方向相同 (B)OB∥O1B1
(C)OB与O1B1不平行 (D)OB与O1B1不一定平行
3.下列四个结论中假命题的个数是( )
①垂直于同一直线的两条直线互相平行;
②平行于同一直线的两直线平行;
③若直线a,b,c满足a∥b,b⊥c,则a⊥c;
④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线.
(A)1 (B)2
(C)3 (D)4DB4.正方体ABCD-A1B1C1D1中,异面直线BC1和CD1所成的角是( )
(A)30° (B)45°
(C)60° (D)90°
5.如图所示,G,H,M,N分别是三棱柱的顶点或所在棱的中点,则表示直线GH与MN是异面直线的图有 .(填序号)?答案:②④C题型一 空间位置关系的判断【例1-1】 已知空间四边形ABCD,AB≠AC,AE是△ABC中BC边上的高,DF是△BCD中BC边上的中线,求证:AE和DF是异面直线.课堂探究解:假设AE和DF不是异面直线,则AE和DF共面,设过AE,DF的平面为β,若E,F重合,则E为BC的中点,所以AB=AC,与AB≠AC相矛盾.若E,F不重合,因为B∈EF,C∈EF,而EF?β,所以B∈β,C∈β,又A∈β,D∈β,所以A,B,C,D四点共面,这与题设ABCD为空间四边形矛盾,综上可知,假设不成立,所以AE与DF为异面直线.【1-2】 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AA1,AB的中点,试判断下列各对线段所在直线的位置关系:(1)AB与CC1;(2)A1B1与DC;(3)A1C与D1B;(4)DC与BD1;(5)D1E与CF.解:(1)因为C∈平面ABCD,AB?平面ABCD,
又C?AB,C1?平面ABCD,所以AB与CC1异面.
(2)因为A1B1∥AB,AB∥DC,所以A1B1∥DC.
(3)因为A1D1∥B1C1,B1C1∥BC,
所以A1D1∥BC,
则A1,B,C,D1在同一平面内.
所以A1C与D1B相交.
(4)因为B∈平面ABCD,DC?平面ABCD,
又B?DC,D1?平面ABCD,所以DC与BD1异面.(5)CF与DA的延长线交于G,连接D1G,
因为AF∥DC,F为AB的中点,所以A为DG的中点.
又AE∥DD1,所以GD1过AA1的中点.
所以直线D1E与CF相交.方法技巧 判定两直线异面的常用方法
(1)定义法:由定义判断两直线不可能在同一平面内;
(2)排除法(反证法):排除两直线共面(平行或相交)的情况.即时训练1-1:正方体ABCD-A1B1C1D1中,与棱AB异面且垂直的棱有( )
(A)8条 (B)6条
(C)4条 (D)3条解析:如图所示,一共有12条棱,其中有三条与AB平行,有四条与AB相交,还剩四条,这四条是CC1,DD1,A1D1,B1C1都是与AB异面且垂直.故选C.题型二公理4及等角定理的应用【例2】 如图所示,在正方体ABCD-A′B′C′D′中,E,F,E′,F′分别是AB,BC,A′B′,B′C′的中点,求证:EE′∥FF′.证明:因为E,E′分别是AB,A′B′的中点,
所以BE∥B′E′,且BE=B′E′,
所以四边形EBB′E′是平行四边形.
所以EE′∥BB′,
同理可证FF′∥BB′,
所以EE′∥FF′.变式探究1:在本例中,若M,N分别是A′D′,C′D′的中点,求证:四边形ACNM是梯形.变式探究2:将本例变为已知E,E′分别是正方体ABCD-A′B′C′D′的棱AD,A′D′的中点,求证:∠BEC=∠B′E′C′.证明:如图所示,连接EE′.
因为E,E′分别是AD,A′D′的中点,
所以AE∥A′E′,且AE=A′E′.
所以四边形AEE′A′是平行四边形.
所以AA′∥EE′,且AA′=EE′.
又因为AA′∥BB′,且AA′=BB′,
所以EE′∥BB′,且EE′=BB′.
所以四边形BEE′B′是平行四边形.所以BE∥B′E′.
同理可证CE∥C′E′.
又∠BEC与∠B′E′C′的两边方向相同,
所以∠BEC=∠B′E′C′.方法技巧 证明两直线平行的常用方法:(1)利用平面几何的结论,如平行四边形的对边,三角形的中位线与底边;(2)定义法:即证明两条直线在同一个平面内且两直线没有公共点;(3)利用公理4:找到一条直线,使所证的直线都与这条直线平行.答案:平行2-2:在正方体ABCD-A1B1C1D1中,E,F分别为AD,AB的中点,M,N分别为B1C1,C1D1的中点.
求证:(1)MC∥A1E,A1F∥CN;(2)∠EA1F=∠NCM.证明:(2)由(1)知A1F∥CN,
MC∥A1E,
又A1E,A1F与CM,CN的方向分别相反,
所以∠EA1F=∠NCM.题型三求异面直线所成的角【例3-1】 在正方体ABCD-A1B1C1D1中,E,F分别是A1B1,B1C1的中点,求异面直线DB1与EF所成角的大小.解:如图所示,连接A1C1,B1D1,并设它们相交于点O,取DD1的中点G,连接OG,A1G,C1G,
则OG∥B1D,EF∥A1C1,
所以∠GOA1为异面直线DB1与EF所成的角(或其补角).
因为GA1=GC1,O为A1C1的中点,
所以GO⊥A1C1.
所以异面直线DB1与EF所成的角为90°.方法技巧 求异面直线所成角的一般步骤:(1)找(或作出)异面直线所成的角——用平移法,若题设中有中点,常考虑中位线.(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的角.(3)结论——设(2)所求角大小为θ.若0°<θ≤90°,则θ即为所求;若90°<θ<180°,则180°-θ即为所求.即时训练3-1:(1)在正方体ABCD-A1B1C1D1中,CC1与BD1所成角的正弦值为 ;?(2)在正方体ABCD-A1B1C1D1中与侧面的对角线AD1成60°角的面对角线有
条.?解析:(2)因为ABCD-A1B1C1D1为正方体,
所以△AD1B1,△AD1C均为等边三角形.
所以AD1与BD,AD1与DC1,AD1与A1B,AD1与DC1,AD1与D1B1,AD1与AB1,AD1与AC,AD1与D1C均成60°角,共8条.
答案:(2)8于是∠EMH=60°,
则∠EMF=2∠EMH=120°.
所以异面直线AD,BC所成的角为∠EMF的补角,即异面直线AD,BC所成的角为60°.
