高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.1.3空间中直线与平面之间的位置关系2.1.4平面与平面之间的位置关系(21张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.1.3空间中直线与平面之间的位置关系2.1.4平面与平面之间的位置关系(21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 16:48:13 | ||
图片预览






文档简介
课件21张PPT。2.1.3 空间中直线与平面之间的位置关系
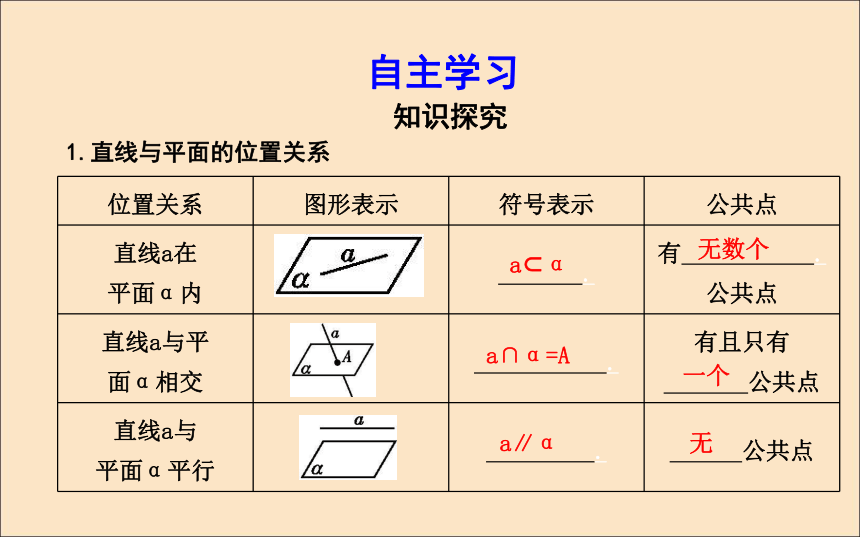
2.1.4 平面与平面之间的位置关系课标要求:1.会判断直线与平面、平面与平面的位置关系.2.会用符号语言和图形语言表示直线和平面、平面和平面的位置关系.自主学习知识探究1.直线与平面的位置关系a?α无数个a∩α=A一个a∥α无探究1:(教师备用)“直线与平面不相交”与“直线与平面没有公共点”是相同的意义吗?
答案:不是.前者包括直线与平面平行及直线在平面内这两种情况,而后者仅指直线与平面平行.
2.直线与平面位置关系的两种分类
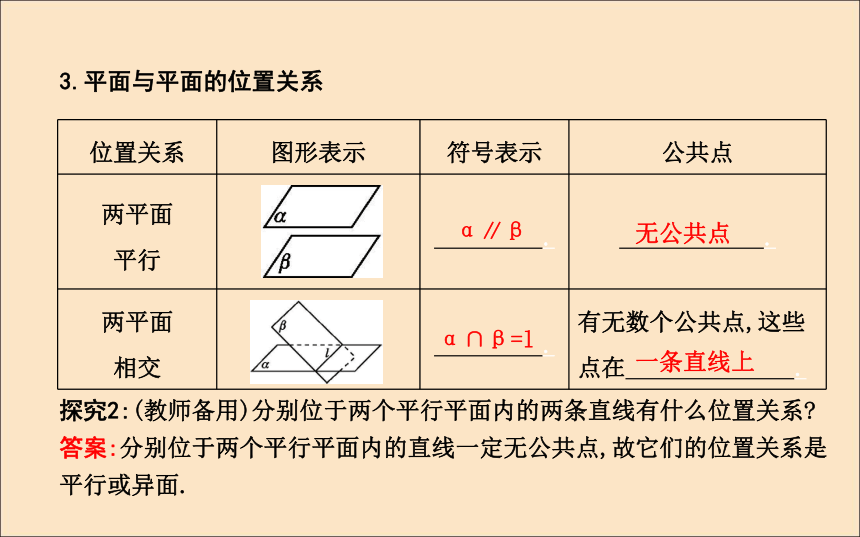
(1)按公共点个数分类3.平面与平面的位置关系α∥β无公共点α∩β=l一条直线上探究2:(教师备用)分别位于两个平行平面内的两条直线有什么位置关系?
答案:分别位于两个平行平面内的直线一定无公共点,故它们的位置关系是平行或异面.自我检测1.若直线l与平面α有公共点,则直线l与平面α的位置关系为( )
(A)l?α
(B)l∥α
(C)l?α或l与α相交
(D)l与α相交
2.棱柱的任意两个侧面的位置关系是( )
(A)相交 (B)平行
(C)平行或异面 (D)平行或相交CD3.若直线a不平行于平面α,则下列结论成立的是( )
(A)α内的所有直线均与a异面
(B)α内不存在与a平行的直线
(C)α内的直线均与a相交
(D)直线a与平面α有公共点D解析:直线a不平行于平面α,即直线a在α内或a与α相交,当a?α时,A,B均不正确,当a与α相交时,α内存在直线与a异面,故C不正确.4.直线a?平面α,直线b?平面α,则a,b的位置关系是 .?答案:平行、相交或异面5.下列命题:①若直线与平面没有公共点,则直线与平面平行;②若直线l在平面α外,则l∥α;③若a?α,α∥β,则β内有无数条直线与直线a平行,其中是真命题的序号是 .?解析:由直线与平面平行的定义可知①正确;由直线与平面的位置关系知②不正确;由平面与平面之间的位置关系可知③正确.
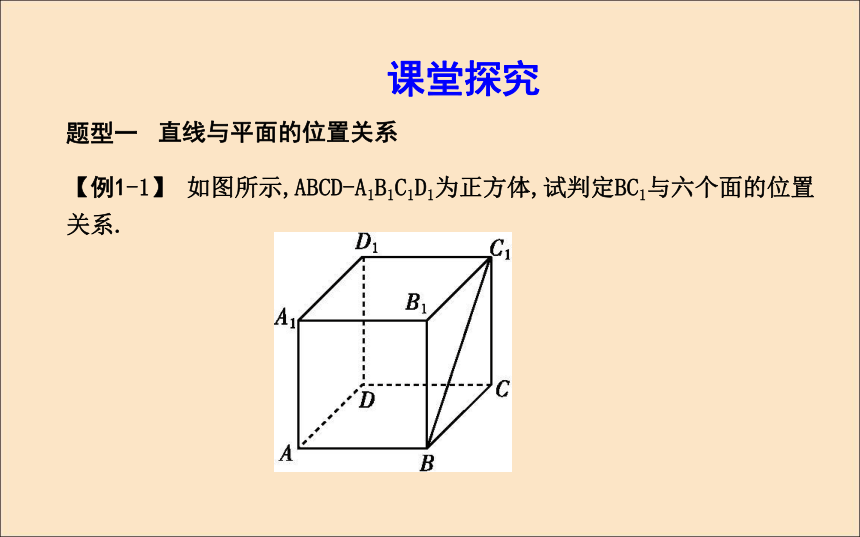
答案:①③题型一直线与平面的位置关系【例1-1】 如图所示,ABCD-A1B1C1D1为正方体,试判定BC1与六个面的位置关系.
课堂探究解:因为B∈面BCC1B1,C1∈面BCC1B1,
所以BC1?面BCC1B1.
又因为BC1与面ADD1A1无公共点,
所以BC1∥面ADD1A1.
因为C1∈面CDD1C1,B?面CDD1C1,
所以BC1与面CDD1C1相交,
同理BC1与面ABB1A相交,
BC1与面ABCD相交,BC1与面A1B1C1D1相交.【1-2】 给出以下命题(其中a,b表示直线,α表示平面):
①若a∥α,b∥α,则a∥b;
②若a∥b,b∥α,则a∥α;
③若a∥α,b?α,则a∥b;
④若α的同侧有两点A,B到平面α的距离相等,则AB∥α.
其中正确命题的个数是( )
(A)0 (B)1
(C)2 (D)3解析:如图,在长方体ABCD-A′B′C′D′中,A′B′∥平面ABCD,B′C′∥平面ABCD,但A′B′与B′C′相交,故①错误;
AB∥A′B′,A′B′∥平面ABCD,但AB?平面ABCD,故②错误;
A′B′∥平面ABCD,BC?平面ABCD,但A′B′与BC异面,故③错误.
④显然正确.误区警示 解决此类问题首先要搞清楚直线与平面各种位置关系的特征,利用其定义作出判断,要有画图意识,并借助空间想象能力进行细致的分析.即时训练1-1:下列说法中,正确的个数是( )
①如果两条平行直线中的一条和一个平面相交,那么另一条也和这个平面相交 ②一条直线和另一条直线平行,它就和经过另一条直线的任何平面平行 ③若直线a在平面α外,则a∥α.
(A)0 (B)1
(C)2 (D)3解析:由直线与平面的位置关系可知①正确;这条直线可能在经过另一条直线的平面内,所以②不正确,对于③包括两种情形,直线a∥α或直线a与α相交,故③不正确.故选B.证明:如图所示,因为a∥b,
所以a和b确定平面β.
因为a∩α=P,
所以平面α和平面β相交于过点P的直线l.
因为在平面β内l与两条平行直线a,b中的一条直线a相交,
所以l必与b相交,
设b∩l=Q,则Q∈α.
又b不在平面α内,
故直线b和平面α相交,相交于Q.1-2:已知:直线a∥直线b,a∩平面α=P,求证:直线b与平面α相交.题型二平面与平面的位置关系【例2-1】 α,β是两个不重合的平面,下面说法中,正确的是( )
(A)平面α内有两条直线a,b都与平面β平行,那么α∥β
(B)平面α内有无数条直线平行于平面β,那么α∥β
(C)若直线a与平面α和平面β都平行,那么α∥β
(D)平面α内所有的直线都与平面β平行,那么α∥β解析:对于A,α与β可能相交或平行,错;对于Β,α与β可能相交或平行,错;对于C,α与β可能相交或平行,错;D符合面面平行的定义,正确.选D.解:(1)两个平面有两种情形
①当两个平面平行时,将空间分成三部分(如图(1));
②当两个平面相交时,将空间分成四部分(如图(2)).【2-2】 一个平面将空间分成两部分,那么两个平面呢?三个平面呢?(2)三个平面有五种情形
①当三个平面互相平行时,将空间分成四部分(如图(3));
②当两个平面平行,第三个平面与它们相交时,将空间分成六部分(如图(4));
③当三个平面相交于同一条直线时,将空间分成六部分(如图(5));
④当三个平面相交于三条直线,且三条交线相交于一点时,将空间分成八部分(如图(6));
⑤当三个平面相交于三条直线,且三条交线相互平行时,将空间分成七部分(如图(7)).【2-3】 一个三棱锥向各面延展成平面后,这些平面将空间分成几部分?答案:1+4+4+6=15部分方法技巧 判断线线、线面、面面的位置关系,要牢牢地抓住其特征与定义、要有画图的意识,结合空间想象能力全方位、多角度地去考虑问题,作出判断.常借助长方体模型进行判断.即时训练2-1:平面α与平面β平行且a?α,下列四种说法中,①a与β内的所有直线都平行;②a与β平行;③a与β内的无数条直线平行,其中正确的个数是( )
(A)0 (B)1 (C)2 (D)3解析:因为α∥β,a?α,所以a与β无公共点,所以a∥β,故②正确,所以a与β内的所有直线都没有公共点,所以a与β内的直线平行或异面,故①不正确,③正确.故选C.2-2:已知平面α∥平面β,若P,Q是α,β之间的两个点,则( )
(A)过P,Q的平面一定与α,β都相交
(B)过P,Q有且仅有一个平面与α,β都平行
(C)过P,Q的平面不一定与α,β都平行
(D)过P,Q可作无数个平面与α,β都平行解析:当过P,Q的直线与α,β相交时,过P,Q的平面一定与平面α,β都相交,排除B,D;当过P,Q的直线与α,β都平行时,可以作唯一的一个平面与α,β都平行,排除A,故选C.
2.1.4 平面与平面之间的位置关系课标要求:1.会判断直线与平面、平面与平面的位置关系.2.会用符号语言和图形语言表示直线和平面、平面和平面的位置关系.自主学习知识探究1.直线与平面的位置关系a?α无数个a∩α=A一个a∥α无探究1:(教师备用)“直线与平面不相交”与“直线与平面没有公共点”是相同的意义吗?
答案:不是.前者包括直线与平面平行及直线在平面内这两种情况,而后者仅指直线与平面平行.
2.直线与平面位置关系的两种分类
(1)按公共点个数分类3.平面与平面的位置关系α∥β无公共点α∩β=l一条直线上探究2:(教师备用)分别位于两个平行平面内的两条直线有什么位置关系?
答案:分别位于两个平行平面内的直线一定无公共点,故它们的位置关系是平行或异面.自我检测1.若直线l与平面α有公共点,则直线l与平面α的位置关系为( )
(A)l?α
(B)l∥α
(C)l?α或l与α相交
(D)l与α相交
2.棱柱的任意两个侧面的位置关系是( )
(A)相交 (B)平行
(C)平行或异面 (D)平行或相交CD3.若直线a不平行于平面α,则下列结论成立的是( )
(A)α内的所有直线均与a异面
(B)α内不存在与a平行的直线
(C)α内的直线均与a相交
(D)直线a与平面α有公共点D解析:直线a不平行于平面α,即直线a在α内或a与α相交,当a?α时,A,B均不正确,当a与α相交时,α内存在直线与a异面,故C不正确.4.直线a?平面α,直线b?平面α,则a,b的位置关系是 .?答案:平行、相交或异面5.下列命题:①若直线与平面没有公共点,则直线与平面平行;②若直线l在平面α外,则l∥α;③若a?α,α∥β,则β内有无数条直线与直线a平行,其中是真命题的序号是 .?解析:由直线与平面平行的定义可知①正确;由直线与平面的位置关系知②不正确;由平面与平面之间的位置关系可知③正确.
答案:①③题型一直线与平面的位置关系【例1-1】 如图所示,ABCD-A1B1C1D1为正方体,试判定BC1与六个面的位置关系.
课堂探究解:因为B∈面BCC1B1,C1∈面BCC1B1,
所以BC1?面BCC1B1.
又因为BC1与面ADD1A1无公共点,
所以BC1∥面ADD1A1.
因为C1∈面CDD1C1,B?面CDD1C1,
所以BC1与面CDD1C1相交,
同理BC1与面ABB1A相交,
BC1与面ABCD相交,BC1与面A1B1C1D1相交.【1-2】 给出以下命题(其中a,b表示直线,α表示平面):
①若a∥α,b∥α,则a∥b;
②若a∥b,b∥α,则a∥α;
③若a∥α,b?α,则a∥b;
④若α的同侧有两点A,B到平面α的距离相等,则AB∥α.
其中正确命题的个数是( )
(A)0 (B)1
(C)2 (D)3解析:如图,在长方体ABCD-A′B′C′D′中,A′B′∥平面ABCD,B′C′∥平面ABCD,但A′B′与B′C′相交,故①错误;
AB∥A′B′,A′B′∥平面ABCD,但AB?平面ABCD,故②错误;
A′B′∥平面ABCD,BC?平面ABCD,但A′B′与BC异面,故③错误.
④显然正确.误区警示 解决此类问题首先要搞清楚直线与平面各种位置关系的特征,利用其定义作出判断,要有画图意识,并借助空间想象能力进行细致的分析.即时训练1-1:下列说法中,正确的个数是( )
①如果两条平行直线中的一条和一个平面相交,那么另一条也和这个平面相交 ②一条直线和另一条直线平行,它就和经过另一条直线的任何平面平行 ③若直线a在平面α外,则a∥α.
(A)0 (B)1
(C)2 (D)3解析:由直线与平面的位置关系可知①正确;这条直线可能在经过另一条直线的平面内,所以②不正确,对于③包括两种情形,直线a∥α或直线a与α相交,故③不正确.故选B.证明:如图所示,因为a∥b,
所以a和b确定平面β.
因为a∩α=P,
所以平面α和平面β相交于过点P的直线l.
因为在平面β内l与两条平行直线a,b中的一条直线a相交,
所以l必与b相交,
设b∩l=Q,则Q∈α.
又b不在平面α内,
故直线b和平面α相交,相交于Q.1-2:已知:直线a∥直线b,a∩平面α=P,求证:直线b与平面α相交.题型二平面与平面的位置关系【例2-1】 α,β是两个不重合的平面,下面说法中,正确的是( )
(A)平面α内有两条直线a,b都与平面β平行,那么α∥β
(B)平面α内有无数条直线平行于平面β,那么α∥β
(C)若直线a与平面α和平面β都平行,那么α∥β
(D)平面α内所有的直线都与平面β平行,那么α∥β解析:对于A,α与β可能相交或平行,错;对于Β,α与β可能相交或平行,错;对于C,α与β可能相交或平行,错;D符合面面平行的定义,正确.选D.解:(1)两个平面有两种情形
①当两个平面平行时,将空间分成三部分(如图(1));
②当两个平面相交时,将空间分成四部分(如图(2)).【2-2】 一个平面将空间分成两部分,那么两个平面呢?三个平面呢?(2)三个平面有五种情形
①当三个平面互相平行时,将空间分成四部分(如图(3));
②当两个平面平行,第三个平面与它们相交时,将空间分成六部分(如图(4));
③当三个平面相交于同一条直线时,将空间分成六部分(如图(5));
④当三个平面相交于三条直线,且三条交线相交于一点时,将空间分成八部分(如图(6));
⑤当三个平面相交于三条直线,且三条交线相互平行时,将空间分成七部分(如图(7)).【2-3】 一个三棱锥向各面延展成平面后,这些平面将空间分成几部分?答案:1+4+4+6=15部分方法技巧 判断线线、线面、面面的位置关系,要牢牢地抓住其特征与定义、要有画图的意识,结合空间想象能力全方位、多角度地去考虑问题,作出判断.常借助长方体模型进行判断.即时训练2-1:平面α与平面β平行且a?α,下列四种说法中,①a与β内的所有直线都平行;②a与β平行;③a与β内的无数条直线平行,其中正确的个数是( )
(A)0 (B)1 (C)2 (D)3解析:因为α∥β,a?α,所以a与β无公共点,所以a∥β,故②正确,所以a与β内的所有直线都没有公共点,所以a与β内的直线平行或异面,故①不正确,③正确.故选C.2-2:已知平面α∥平面β,若P,Q是α,β之间的两个点,则( )
(A)过P,Q的平面一定与α,β都相交
(B)过P,Q有且仅有一个平面与α,β都平行
(C)过P,Q的平面不一定与α,β都平行
(D)过P,Q可作无数个平面与α,β都平行解析:当过P,Q的直线与α,β相交时,过P,Q的平面一定与平面α,β都相交,排除B,D;当过P,Q的直线与α,β都平行时,可以作唯一的一个平面与α,β都平行,排除A,故选C.
