高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.2.1直线与平面平行的判定(21张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.2.1直线与平面平行的判定(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 16:46:05 | ||
图片预览







文档简介
课件21张PPT。2.2 直线、平面平行的判定及其性质
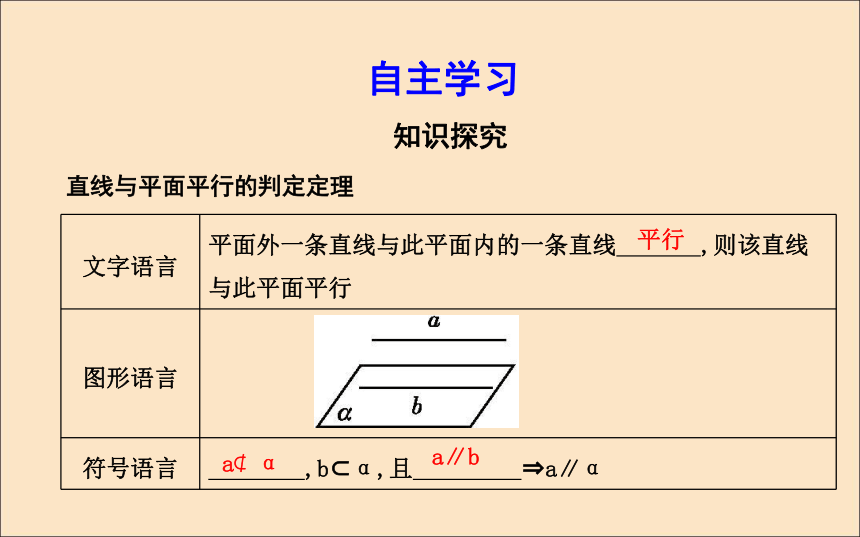
2.2.1 直线与平面平行的判定课标要求:1.理解直线与平面平行的判定定理.2.能运用直线与平面平行的判定定理证明一些空间位置关系的命题.自主学习知识探究直线与平面平行的判定定理平行a?α a∥b 探究:(教师备用)若a∥b,a∥α,则b∥α,这个推理正确吗?
答案:不正确.b可能在α内.自我检测1.若A是直线m外一点,过A且与m平行的平面( )
(A)存在无数个 (B)不存在
(C)存在但只有一个 (D)只存在两个
2.下列命题,能得出直线m与平面α平行的是( )
(A)直线m与平面α内的两条直线平行
(B)直线m 与平面α内无数条直线平行
(C)直线m与平面α没有公共点
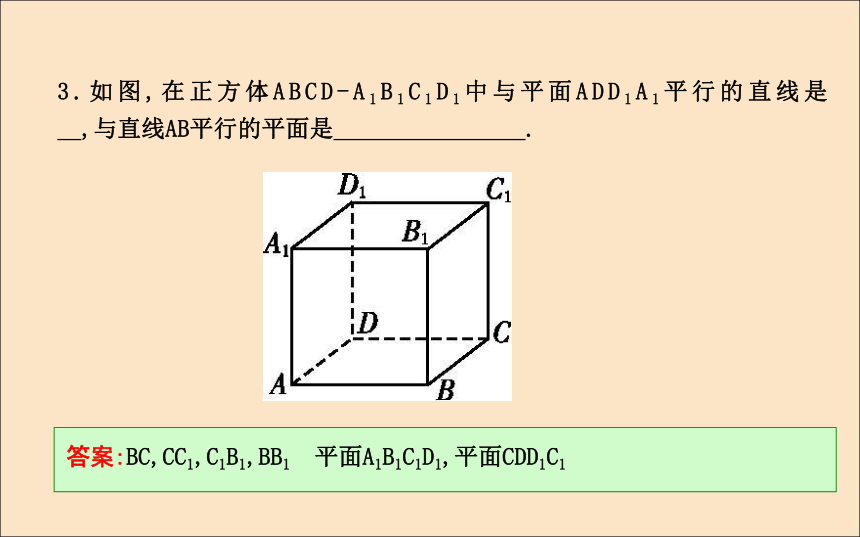
(D)直线m与平面α内的一条直线平行AC3.如图,在正方体ABCD-A1B1C1D1中与平面ADD1A1平行的直线是 ,与直线AB平行的平面是 .?答案:BC,CC1,C1B1,BB1 平面A1B1C1D1,平面CDD1C14.设m,n是平面α外的两条直线,给出下列三个论断:①m∥n;②m∥α;③n∥α,以其中两个为条件,余下一个为结论,可以构成三个命题,请你写出你认为正确的一个命题是 .?答案:①②?③题型一线面平行的判定定理的理解【例1-1】 下列说法中正确的是( )
(A)若直线l平行于平面α内的无数条直线,则l∥α
(B)若直线a在平面α外,则a∥α
(C)若直线a∥b,b?α,则a∥α
(D)若直线a∥b,b?α,那么直线a平行于平面α内的无数条直线课堂探究解析:选项A中,直线l?α时l与α不平行;
直线在平面外包括直线与平面平行和直线与平面相交两种情况,所以选项B不正确;
选项C中直线a可能在平面α内;选项D正确.故选D.【1-2】 一条直线l上有相异三个点A,B,C到平面α的距离相等,那么直线l与平面α的位置关系是( )
(A)l∥α (B)l⊥α
(C)l与α相交但不垂直 (D)l∥α或l?α解析:l∥α时,直线l上任意一点到α的距离都相等.l?α时,直线l上所有的点到α的距离都是0.l⊥α时,直线l上有两个点到α的距离相等.l与α斜交时,也只能有两点到α的距离相等.故选D.即时训练1-1:有以下三种说法,其中正确的是( )
①若直线a与平面α相交,则α内不存在与a平行的直线;②若直线b∥平面α,直线a与直线b垂直,则直线a不可能与α平行;③直线a,b满足a∥α,且b?α,则a平行于经过b的任何平面.
(A)①② (B)①③ (C)②③ (D)①解析:①正确.②错误,反例如图(1)所示.③错误,反例如图(2)所示,a,b可能在同一平面内.故选D.题型二直线与平面平行的判定【例2-1】 (12分)如图,M,N分别是底面为矩形的四棱锥P-ABCD的棱AB,PC的中点,求证:MN∥平面PAD.方法技巧 利用直线和平面平行的判定定理来证明线面平行,关键是寻找平面内与已知直线平行的直线,常利用平行四边形的性质、三角形与梯形中位线性质、平行线截线段成比例定理、平行公理等.变式探究:改变本例中的设题背景,如在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.求证:BD∥平面FGH.证明:如图,连接DG,CD,设CD∩GF=M,连接MH.
在三棱台DEF-ABC中,
AB=2DE,G为AC的中点,
可得DF∥GC,DF=GC,
所以四边形DFCG为平行四边形.
即M为CD的中点,
又H为BC的中点,所以HM∥BD.
又HM?平面FGH,BD?平面FGH,
所以BD∥平面FGH.【2-2】 已知公共边为AB的两个全等的矩形ABCD和ABEF不在同一平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,如图所示.求证:PQ∥平面CBE.即时训练2-1:如图,三棱柱ABC-A1B1C1中,D为C1B的中点,P为AB的中点,证明DP∥平面ACC1A1.证明:连接AC1,
因为P为AB的中点,D为C1B的中点,
所以DP∥AC1,
又因为AC1?平面ACC1A1,DP?平面ACC1A1,
所以DP∥平面ACC1A1.
2-2:一个多面体的三视图及直观图如图所示,M,N分别是A1B,B1C1的中点,求证:MN∥平面ACC1A1.证明:由三视图可知该多面体是侧棱长为a,底面为等腰直角三角形的直三棱柱,AC=BC=a,∠ACB=90°.
连接AB1,AC1,由平行四边形的性质可知AB1与A1B相交于点M.
在△B1AC1中,
因为M,N分别是AB1,B1C1的中点,
所以MN∥AC1,
又MN?平面ACC1A1,AC1?平面ACC1A1,
所以MN∥平面ACC1A1.
2.2.1 直线与平面平行的判定课标要求:1.理解直线与平面平行的判定定理.2.能运用直线与平面平行的判定定理证明一些空间位置关系的命题.自主学习知识探究直线与平面平行的判定定理平行a?α a∥b 探究:(教师备用)若a∥b,a∥α,则b∥α,这个推理正确吗?
答案:不正确.b可能在α内.自我检测1.若A是直线m外一点,过A且与m平行的平面( )
(A)存在无数个 (B)不存在
(C)存在但只有一个 (D)只存在两个
2.下列命题,能得出直线m与平面α平行的是( )
(A)直线m与平面α内的两条直线平行
(B)直线m 与平面α内无数条直线平行
(C)直线m与平面α没有公共点
(D)直线m与平面α内的一条直线平行AC3.如图,在正方体ABCD-A1B1C1D1中与平面ADD1A1平行的直线是 ,与直线AB平行的平面是 .?答案:BC,CC1,C1B1,BB1 平面A1B1C1D1,平面CDD1C14.设m,n是平面α外的两条直线,给出下列三个论断:①m∥n;②m∥α;③n∥α,以其中两个为条件,余下一个为结论,可以构成三个命题,请你写出你认为正确的一个命题是 .?答案:①②?③题型一线面平行的判定定理的理解【例1-1】 下列说法中正确的是( )
(A)若直线l平行于平面α内的无数条直线,则l∥α
(B)若直线a在平面α外,则a∥α
(C)若直线a∥b,b?α,则a∥α
(D)若直线a∥b,b?α,那么直线a平行于平面α内的无数条直线课堂探究解析:选项A中,直线l?α时l与α不平行;
直线在平面外包括直线与平面平行和直线与平面相交两种情况,所以选项B不正确;
选项C中直线a可能在平面α内;选项D正确.故选D.【1-2】 一条直线l上有相异三个点A,B,C到平面α的距离相等,那么直线l与平面α的位置关系是( )
(A)l∥α (B)l⊥α
(C)l与α相交但不垂直 (D)l∥α或l?α解析:l∥α时,直线l上任意一点到α的距离都相等.l?α时,直线l上所有的点到α的距离都是0.l⊥α时,直线l上有两个点到α的距离相等.l与α斜交时,也只能有两点到α的距离相等.故选D.即时训练1-1:有以下三种说法,其中正确的是( )
①若直线a与平面α相交,则α内不存在与a平行的直线;②若直线b∥平面α,直线a与直线b垂直,则直线a不可能与α平行;③直线a,b满足a∥α,且b?α,则a平行于经过b的任何平面.
(A)①② (B)①③ (C)②③ (D)①解析:①正确.②错误,反例如图(1)所示.③错误,反例如图(2)所示,a,b可能在同一平面内.故选D.题型二直线与平面平行的判定【例2-1】 (12分)如图,M,N分别是底面为矩形的四棱锥P-ABCD的棱AB,PC的中点,求证:MN∥平面PAD.方法技巧 利用直线和平面平行的判定定理来证明线面平行,关键是寻找平面内与已知直线平行的直线,常利用平行四边形的性质、三角形与梯形中位线性质、平行线截线段成比例定理、平行公理等.变式探究:改变本例中的设题背景,如在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.求证:BD∥平面FGH.证明:如图,连接DG,CD,设CD∩GF=M,连接MH.
在三棱台DEF-ABC中,
AB=2DE,G为AC的中点,
可得DF∥GC,DF=GC,
所以四边形DFCG为平行四边形.
即M为CD的中点,
又H为BC的中点,所以HM∥BD.
又HM?平面FGH,BD?平面FGH,
所以BD∥平面FGH.【2-2】 已知公共边为AB的两个全等的矩形ABCD和ABEF不在同一平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,如图所示.求证:PQ∥平面CBE.即时训练2-1:如图,三棱柱ABC-A1B1C1中,D为C1B的中点,P为AB的中点,证明DP∥平面ACC1A1.证明:连接AC1,
因为P为AB的中点,D为C1B的中点,
所以DP∥AC1,
又因为AC1?平面ACC1A1,DP?平面ACC1A1,
所以DP∥平面ACC1A1.
2-2:一个多面体的三视图及直观图如图所示,M,N分别是A1B,B1C1的中点,求证:MN∥平面ACC1A1.证明:由三视图可知该多面体是侧棱长为a,底面为等腰直角三角形的直三棱柱,AC=BC=a,∠ACB=90°.
连接AB1,AC1,由平行四边形的性质可知AB1与A1B相交于点M.
在△B1AC1中,
因为M,N分别是AB1,B1C1的中点,
所以MN∥AC1,
又MN?平面ACC1A1,AC1?平面ACC1A1,
所以MN∥平面ACC1A1.
