高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.2.2平面与平面平行的判定(22张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.2.2平面与平面平行的判定(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 16:49:23 | ||
图片预览







文档简介
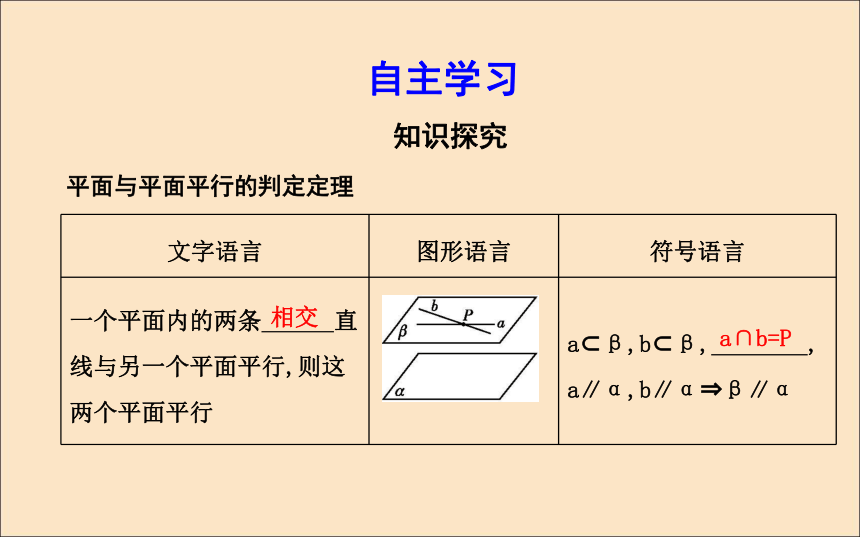
课件22张PPT。2.2.2 平面与平面平行的判定课标要求:1.理解平面与平面平行的判定定理.2.能应用面面平行的判定定理证明一些空间位置关系的简单命题.自主学习知识探究平面与平面平行的判定定理相交a∩b=P 探究1:(教师备用)如果两个平面都与第三个平面平行,这两个平面平行吗?
答案:平行.
探究2:(教师备用)如果两个平面都平行于某一条直线,这两个平面平行吗?
答案:不一定平行.自我检测1.若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( )
(A)一定平行 (B)一定相交
(C)平行或相交 (D)以上判断都不对
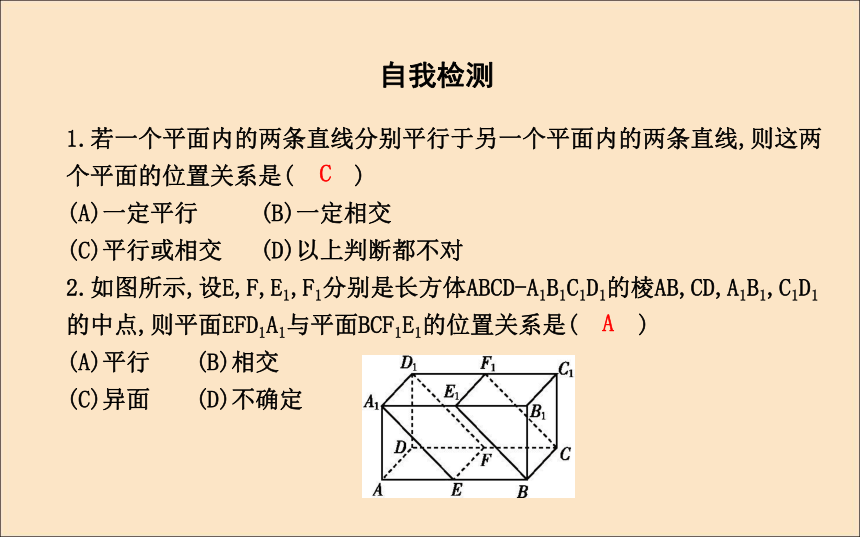
2.如图所示,设E,F,E1,F1分别是长方体ABCD-A1B1C1D1的棱AB,CD,A1B1,C1D1的中点,则平面EFD1A1与平面BCF1E1的位置关系是( )
(A)平行 (B)相交
(C)异面 (D)不确定CA3.平面α内有两条直线a和b,且a∥β,b∥β,则α与β的位置关系是 .?答案:平行或相交4.已知三个平面α,β,γ,一条直线l,要得到α∥β,下列条件中合适的是( )
(A)l∥α,l∥β且l∥γ (B)l?γ,且l∥α,l∥β
(C)α∥γ,且β∥γ (D)l与α,β所成的角相等C5.已知a,b是两条直线,α,β是两个平面,Ρ是一个点,若a∥β,b∥β,a?
α,b?α,且 (填上一个条件即可),则有α∥β.?答案:a∩b=P题型一 对面面平行判定定理的理解【例1-1】 已知直线l,m,平面α,β,下列命题正确的是( )
(A)l∥β,l?α?α∥β
(B)l∥β,m∥β,l?α,m?α?α∥β
(C)l∥m,l?α,m?β?α∥β
(D)l∥β,m∥β,l?α,m?α,l∩m=M?α∥β课堂探究解析:如图所示,长方体ABCD-A1B1C1D1中,AB∥CD,则AB∥平面DC1,AB?平面AC,但是平面AC与平面DC1不平行,所以选项A错误;取BB1中点E,CC1的中点F,则可证EF∥平面AC,B1C1∥平面AC.又EF?平面BC1,B1C1?平面BC1,但是平面AC与平面BC1不平行,所以选项B错误;可证AD∥B1C1,AD?平面AC,B1C1?平面BC1,又平面AC与平面BC1不平行,所以选项C错误;很明显选项D是面面平行的判定定理,所以选项D正确.故选D.【1-2】 下列命题中正确的是( )
①若一个平面内有两条直线与另一个平面平行,则这两个平面平行;
②若一个平面内有无数条直线与另一个平面平行,则这两个平面平行;
③若一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行;
④若一个平面内的两条相交直线都与另一个平面平行,则这两个平面平行.
(A)①③ (B)②④
(C)②③④ (D)③④解析:①②中两个平面还可以相交,故①②错误;由两个平面平行的定义,知③正确;由两个平面平行的判定定理,知④正确.故选D.方法技巧 解决此类问题的关键有两点:(1)借助常见几何体进行分析,使得抽象问题具体化.(2)把握住面面平行的判定定理的关键“一个平面内两条相交直线均平行于另一个平面”.即时训练1-1:平面α与平面β平行的条件可以是( )
(A)α内有无穷多条直线都与β平行
(B)直线a∥α,a∥β,且直线a不在α内,也不在β内
(C)α内的任何直线都与β平行
(D)直线a在α内,直线b在β内,且a∥β,b∥α1-2:给出下列三个结论:
①一个平面α内有两条不平行的直线都平行于另一个平面β,则α∥β;②过平面α外一点且与α平行的所有直线在同一平面内;③如果平面α∩γ=a,平面γ∩β=b,a∥b,则α∥β,其中不正确的结论有 个.?解析:①,②正确;满足条件α∩γ=a,β∩γ=b,a∥b时,可能有α∥β,也可能有α与β相交,故③错误.
答案:1题型二平面与平面平行的判定【例2】 (12分)如图所示,已知正方体ABCD-A1B1C1D1.
(1)求证:平面A1BD∥平面B1D1C.(2)若E,F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.规范解答:(2)由BD∥B1D1,得BD∥平面EB1D1.………………5分
取BB1的中点G,连接AG,GF,易得AE∥B1G, …………………6分
又因为AE=B1G,所以四边形AEB1G是平行四边形, …………7分
所以B1E∥AG.易得GF∥AD. …………………………………8分
又因为GF=AD,
所以四边形ADFG是平行四边形, ……………………………9分
所以AG∥DF,所以B1E∥DF, …………………………………10分
所以DF∥平面EB1D1.
又因为BD∩DF=D,所以平面EB1D1∥平面FBD. ………………12分方法技巧即时训练2-1:已知四棱锥P-ABCD中,底面ABCD为平行四边形.点M,N,Q分别在PA,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD,求证:平面MNQ∥平面PBC.证明:因为PM∶MA=BN∶ND=PQ∶QD,
所以MQ∥AD,NQ∥BP,
而BP?平面PBC,NQ?平面PBC,
所以NQ∥平面PBC,
又因为四边形ABCD为平行四边形,BC∥AD,
所以MQ∥BC.
而BC?平面PBC,MQ?平面PBC,
所以MQ∥平面PBC.
又MQ∩NQ=Q,
所以平面MNQ∥平面PBC.
答案:平行.
探究2:(教师备用)如果两个平面都平行于某一条直线,这两个平面平行吗?
答案:不一定平行.自我检测1.若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( )
(A)一定平行 (B)一定相交
(C)平行或相交 (D)以上判断都不对
2.如图所示,设E,F,E1,F1分别是长方体ABCD-A1B1C1D1的棱AB,CD,A1B1,C1D1的中点,则平面EFD1A1与平面BCF1E1的位置关系是( )
(A)平行 (B)相交
(C)异面 (D)不确定CA3.平面α内有两条直线a和b,且a∥β,b∥β,则α与β的位置关系是 .?答案:平行或相交4.已知三个平面α,β,γ,一条直线l,要得到α∥β,下列条件中合适的是( )
(A)l∥α,l∥β且l∥γ (B)l?γ,且l∥α,l∥β
(C)α∥γ,且β∥γ (D)l与α,β所成的角相等C5.已知a,b是两条直线,α,β是两个平面,Ρ是一个点,若a∥β,b∥β,a?
α,b?α,且 (填上一个条件即可),则有α∥β.?答案:a∩b=P题型一 对面面平行判定定理的理解【例1-1】 已知直线l,m,平面α,β,下列命题正确的是( )
(A)l∥β,l?α?α∥β
(B)l∥β,m∥β,l?α,m?α?α∥β
(C)l∥m,l?α,m?β?α∥β
(D)l∥β,m∥β,l?α,m?α,l∩m=M?α∥β课堂探究解析:如图所示,长方体ABCD-A1B1C1D1中,AB∥CD,则AB∥平面DC1,AB?平面AC,但是平面AC与平面DC1不平行,所以选项A错误;取BB1中点E,CC1的中点F,则可证EF∥平面AC,B1C1∥平面AC.又EF?平面BC1,B1C1?平面BC1,但是平面AC与平面BC1不平行,所以选项B错误;可证AD∥B1C1,AD?平面AC,B1C1?平面BC1,又平面AC与平面BC1不平行,所以选项C错误;很明显选项D是面面平行的判定定理,所以选项D正确.故选D.【1-2】 下列命题中正确的是( )
①若一个平面内有两条直线与另一个平面平行,则这两个平面平行;
②若一个平面内有无数条直线与另一个平面平行,则这两个平面平行;
③若一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行;
④若一个平面内的两条相交直线都与另一个平面平行,则这两个平面平行.
(A)①③ (B)②④
(C)②③④ (D)③④解析:①②中两个平面还可以相交,故①②错误;由两个平面平行的定义,知③正确;由两个平面平行的判定定理,知④正确.故选D.方法技巧 解决此类问题的关键有两点:(1)借助常见几何体进行分析,使得抽象问题具体化.(2)把握住面面平行的判定定理的关键“一个平面内两条相交直线均平行于另一个平面”.即时训练1-1:平面α与平面β平行的条件可以是( )
(A)α内有无穷多条直线都与β平行
(B)直线a∥α,a∥β,且直线a不在α内,也不在β内
(C)α内的任何直线都与β平行
(D)直线a在α内,直线b在β内,且a∥β,b∥α1-2:给出下列三个结论:
①一个平面α内有两条不平行的直线都平行于另一个平面β,则α∥β;②过平面α外一点且与α平行的所有直线在同一平面内;③如果平面α∩γ=a,平面γ∩β=b,a∥b,则α∥β,其中不正确的结论有 个.?解析:①,②正确;满足条件α∩γ=a,β∩γ=b,a∥b时,可能有α∥β,也可能有α与β相交,故③错误.
答案:1题型二平面与平面平行的判定【例2】 (12分)如图所示,已知正方体ABCD-A1B1C1D1.
(1)求证:平面A1BD∥平面B1D1C.(2)若E,F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.规范解答:(2)由BD∥B1D1,得BD∥平面EB1D1.………………5分
取BB1的中点G,连接AG,GF,易得AE∥B1G, …………………6分
又因为AE=B1G,所以四边形AEB1G是平行四边形, …………7分
所以B1E∥AG.易得GF∥AD. …………………………………8分
又因为GF=AD,
所以四边形ADFG是平行四边形, ……………………………9分
所以AG∥DF,所以B1E∥DF, …………………………………10分
所以DF∥平面EB1D1.
又因为BD∩DF=D,所以平面EB1D1∥平面FBD. ………………12分方法技巧即时训练2-1:已知四棱锥P-ABCD中,底面ABCD为平行四边形.点M,N,Q分别在PA,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD,求证:平面MNQ∥平面PBC.证明:因为PM∶MA=BN∶ND=PQ∶QD,
所以MQ∥AD,NQ∥BP,
而BP?平面PBC,NQ?平面PBC,
所以NQ∥平面PBC,
又因为四边形ABCD为平行四边形,BC∥AD,
所以MQ∥BC.
而BC?平面PBC,MQ?平面PBC,
所以MQ∥平面PBC.
又MQ∩NQ=Q,
所以平面MNQ∥平面PBC.
