高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.2.4平面与平面平行的性质(28张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.2.4平面与平面平行的性质(28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 00:00:00 | ||
图片预览







文档简介
课件28张PPT。2.2.4 平面与平面平行的性质课标要求:1.理解平面与平面平行的性质定理及含义.2.能运用面面平行的性质定理,证明一些空间平行关系的简单命题.自主学习知识探究1.平面与平面平行的性质定理平行a∥b探究:(教师备用)如果两个平面平行,那么其中一个平面内的直线和另一个平面有什么样的位置关系?
答案:平行.
2.两个平面平行的其他性质
(1)两个平面平行,其中一个平面内的任意一条直线都平行于另一个平面;
(2)夹在两个平行平面间的平行线段长度相等;
(3)经过平面外一点有且只有一个平面与已知平面平行;
(4)两条直线被三个平行平面所截,截得的对应线段成比例;
(5)如果两个平面分别平行第三个平面,那么这两个平面互相平行.自我检测1.设有不同的直线a,b和不同的平面α,β,γ,给出下列三个命题,其中正确的命题有( )
①若a∥α,b∥α,则a∥b ②若a∥α,a∥β,则α∥β ③若α∥β,
a?α,则a∥β
(A)0个 (B)1个 (C)2个 (D)3个
2.已知平面α∥平面β,若两条直线m,n分别在平面α,β内,则m,n的关系不可能是( )
(A)平行 (B)相交
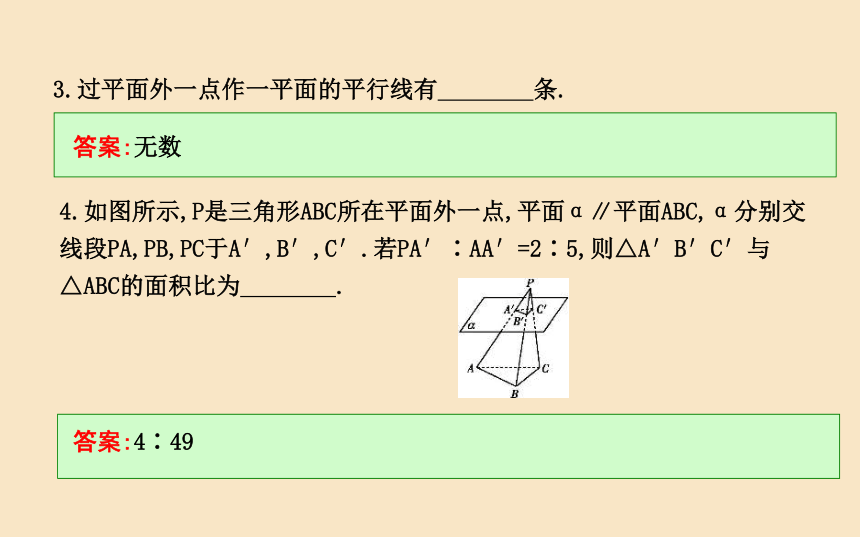
(C)异面 (D)平行或异面BB3.过平面外一点作一平面的平行线有 条.?答案:无数4.如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于A′,B′,C′.若PA′∶AA′=2∶5,则△A′B′C′与△ABC的面积比为 .?答案:4∶495.已知a,b表示两条不同直线,α,β,γ表示三个不重合的平面,给出下列命题:
①若α∩γ=a,β∩γ=b,且a∥b,则α∥β;
②若a,b相交且都在α,β外,a∥α,b∥α,a∥β,b∥β,则α∥β;
③若a?α,a∥β,α∩β=b,则a∥b.
其中正确命题的序号是 .?解析:①若α∩γ=a,β∩γ=b,且a∥b,α,β有可能相交,所以不正确.
②正确,因为在空间确定一个点O,过O作a,b的平行线a′,b′.过a′,b′的平面为γ,所以a∥a′,b∥b′,
因为a∥α,a∥β,b∥α,b∥β,所以γ∥α,γ∥β,所以α∥β.
③正确,若a?α,a∥β,α∩β=b,根据线面平行的性质定理,可得a∥b.
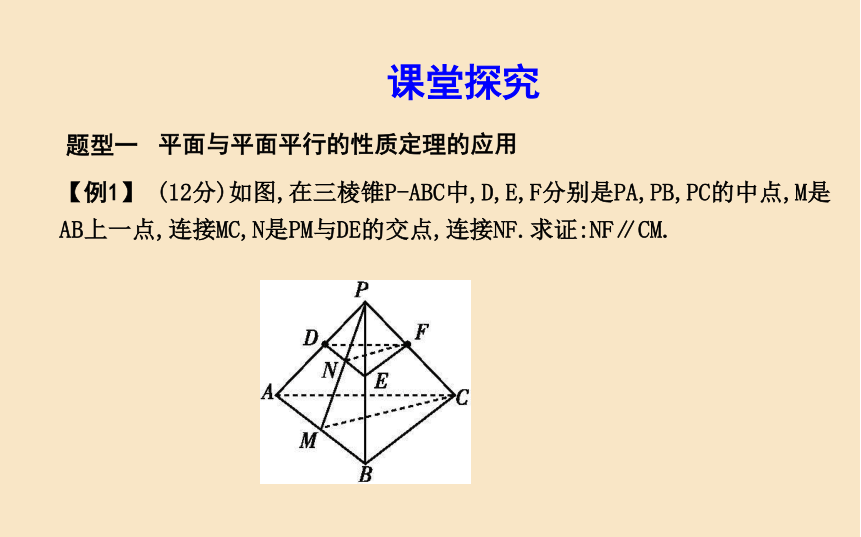
答案:②③题型一平面与平面平行的性质定理的应用【例1】 (12分)如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点,M是AB上一点,连接MC,N是PM与DE的交点,连接NF.求证:NF∥CM.课堂探究规范解答:因为D,E,F分别为PA,PB,PC的中点,所以DE∥AB,又DE?平面ABC,AB?平面ABC,所以DE∥平面ABC,………………………………4分
同理EF∥平面ABC,又DE∩EF=E,所以平面DEF∥平面ABC,…………8分
又平面PMC∩平面ABC=MC,平面PMC∩平面DEF=NF,由面面平行的性质定理得,NF∥MC.……………………………………………………………12分变式探究:将本例中的三棱锥改为长方体,如图是长方体被一平面所截得到的几何体,四边形EFGH为截面,则四边形EFGH的形状为 .?解析:因为平面ABFE∥平面CDHG,平面EFGH与两平面分别交于EF,GH.由面面平行的性质定理得EF∥GH,同理可得EH∥FG,所以四边形EFGH为平行四边形.
答案:平行四边形方法技巧 面面平行的性质定理是由面面平行得到线线平行.证明线线平行的关键是把要证明的直线看作是平面的交线,所以构造三个平面:即两个平行平面,一个经过两直线的平面,有时需要添加辅助面.即时训练1-1:已知如图所示,三棱柱ABC-A1B1C1中,点D,D1分别为AC,A1C1上的点.若平面BC1D∥平面AB1D1,求 的值.1-2:如图,平面四边形ABCD的四个顶点A,B,C,D均在平行四边形A′B′C′D′所确定的一个平面α外,且AA′,BB′,CC′,DD′互相平行.
求证:四边形ABCD是平行四边形.证明:在?A′B′C′D′中,A′B′∥C′D′,
因为A′B′?平面C′D′DC,C′D′?平面C′D′DC,
所以A′B′∥平面C′D′DC.
同理A′A∥平面C′D′DC.
又A′A∩A′B′=A′,
所以平面A′B′BA∥平面C′D′DC.
因为平面ABCD∩平面A′B′BA=AB,
平面ABCD∩平面C′D′DC=CD,
所以AB∥CD.同理AD∥BC.
所以四边形ABCD是平行四边形.题型二平行关系的综合应用【例2-1】 已知平面α∥平面β,点A,C∈α,点B,D∈β,直线AB,CD交于点S,且SA=8,SB=9,CD=34.
(1)若点S在平面α,β之间,则SC= ;?答案:(1)16 (2)若点S不在平面,α,β之间,则SC= .?答案:(2)272【2-2】 (12分)如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
(1)求证:PQ∥平面DCC1D1;规范解答:(1)法一 如图,连接AC,CD1.
因为P,Q分别是AD1,AC的中点,
所以PQ∥CD1 .………………………………1分
又PQ?平面DCC1D1, …………………………2分
CD1?平面DCC1D1, …………………………3分
所以PQ∥平面DCC1D1. ……………………4分
法二 取AD的中点G,连接PG,GQ,
则有PG∥DD1,GQ∥DC,且PG∩GQ=G, ………1分
所以平面PGQ∥平面DCC1D1. ………………2分
又PQ?平面PGQ,
所以PQ∥平面DCC1D1. ………………………4分(2)求PQ的长;
(3)求证:EF∥平面BB1D1D.法二 取B1C1的中点E1,连接EE1,FE1,
则有FE1∥B1D1,EE1∥BB1,且FE1∩EE1=E1,
所以平面EE1F∥平面BB1D1D.…………10分
又EF?平面EE1F,
所以EF∥平面BB1D1D.…………………12分方法技巧 直线与平面平行,平面与平面平行的判定定理、性质定理,揭示了线线平行、线面平行、面面平行之间的转化关系,具体转化过程如图所示.即时训练2-1:如图所示,平面α∥平面β,△ABC,△A1B1C1分别在平面α,β内,线段AA1,BB1,CC1相交于点O,点O在α,β之间,若AB=2,AC=1,OA∶OA1=
3∶2,且BA⊥AC,则△A1B1C1的面积为 .?2-2:如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?解:如图,设平面D1BQ∩平面ADD1A1=D1M,点M在AA1上,平面D1BQ∩平面BCC1B1=BQ,平面ADD1A1∥平面BCC1B1,由面面平行的性质定理可得BQ∥D1M.
假设平面D1BQ∥平面PAO,由平面D1BQ∩平面ADD1A1=D1M,平面PAO∩平面ADD1A1=AP,可得AP∥D1M,所以BQ∥D1M∥AP.因为P为DD1的中点,所以M为AA1的中点,Q为CC1的中点,故当Q为CC1的中点时,平面D1BQ∥平面PAO.
答案:平行.
2.两个平面平行的其他性质
(1)两个平面平行,其中一个平面内的任意一条直线都平行于另一个平面;
(2)夹在两个平行平面间的平行线段长度相等;
(3)经过平面外一点有且只有一个平面与已知平面平行;
(4)两条直线被三个平行平面所截,截得的对应线段成比例;
(5)如果两个平面分别平行第三个平面,那么这两个平面互相平行.自我检测1.设有不同的直线a,b和不同的平面α,β,γ,给出下列三个命题,其中正确的命题有( )
①若a∥α,b∥α,则a∥b ②若a∥α,a∥β,则α∥β ③若α∥β,
a?α,则a∥β
(A)0个 (B)1个 (C)2个 (D)3个
2.已知平面α∥平面β,若两条直线m,n分别在平面α,β内,则m,n的关系不可能是( )
(A)平行 (B)相交
(C)异面 (D)平行或异面BB3.过平面外一点作一平面的平行线有 条.?答案:无数4.如图所示,P是三角形ABC所在平面外一点,平面α∥平面ABC,α分别交线段PA,PB,PC于A′,B′,C′.若PA′∶AA′=2∶5,则△A′B′C′与△ABC的面积比为 .?答案:4∶495.已知a,b表示两条不同直线,α,β,γ表示三个不重合的平面,给出下列命题:
①若α∩γ=a,β∩γ=b,且a∥b,则α∥β;
②若a,b相交且都在α,β外,a∥α,b∥α,a∥β,b∥β,则α∥β;
③若a?α,a∥β,α∩β=b,则a∥b.
其中正确命题的序号是 .?解析:①若α∩γ=a,β∩γ=b,且a∥b,α,β有可能相交,所以不正确.
②正确,因为在空间确定一个点O,过O作a,b的平行线a′,b′.过a′,b′的平面为γ,所以a∥a′,b∥b′,
因为a∥α,a∥β,b∥α,b∥β,所以γ∥α,γ∥β,所以α∥β.
③正确,若a?α,a∥β,α∩β=b,根据线面平行的性质定理,可得a∥b.
答案:②③题型一平面与平面平行的性质定理的应用【例1】 (12分)如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点,M是AB上一点,连接MC,N是PM与DE的交点,连接NF.求证:NF∥CM.课堂探究规范解答:因为D,E,F分别为PA,PB,PC的中点,所以DE∥AB,又DE?平面ABC,AB?平面ABC,所以DE∥平面ABC,………………………………4分
同理EF∥平面ABC,又DE∩EF=E,所以平面DEF∥平面ABC,…………8分
又平面PMC∩平面ABC=MC,平面PMC∩平面DEF=NF,由面面平行的性质定理得,NF∥MC.……………………………………………………………12分变式探究:将本例中的三棱锥改为长方体,如图是长方体被一平面所截得到的几何体,四边形EFGH为截面,则四边形EFGH的形状为 .?解析:因为平面ABFE∥平面CDHG,平面EFGH与两平面分别交于EF,GH.由面面平行的性质定理得EF∥GH,同理可得EH∥FG,所以四边形EFGH为平行四边形.
答案:平行四边形方法技巧 面面平行的性质定理是由面面平行得到线线平行.证明线线平行的关键是把要证明的直线看作是平面的交线,所以构造三个平面:即两个平行平面,一个经过两直线的平面,有时需要添加辅助面.即时训练1-1:已知如图所示,三棱柱ABC-A1B1C1中,点D,D1分别为AC,A1C1上的点.若平面BC1D∥平面AB1D1,求 的值.1-2:如图,平面四边形ABCD的四个顶点A,B,C,D均在平行四边形A′B′C′D′所确定的一个平面α外,且AA′,BB′,CC′,DD′互相平行.
求证:四边形ABCD是平行四边形.证明:在?A′B′C′D′中,A′B′∥C′D′,
因为A′B′?平面C′D′DC,C′D′?平面C′D′DC,
所以A′B′∥平面C′D′DC.
同理A′A∥平面C′D′DC.
又A′A∩A′B′=A′,
所以平面A′B′BA∥平面C′D′DC.
因为平面ABCD∩平面A′B′BA=AB,
平面ABCD∩平面C′D′DC=CD,
所以AB∥CD.同理AD∥BC.
所以四边形ABCD是平行四边形.题型二平行关系的综合应用【例2-1】 已知平面α∥平面β,点A,C∈α,点B,D∈β,直线AB,CD交于点S,且SA=8,SB=9,CD=34.
(1)若点S在平面α,β之间,则SC= ;?答案:(1)16 (2)若点S不在平面,α,β之间,则SC= .?答案:(2)272【2-2】 (12分)如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
(1)求证:PQ∥平面DCC1D1;规范解答:(1)法一 如图,连接AC,CD1.
因为P,Q分别是AD1,AC的中点,
所以PQ∥CD1 .………………………………1分
又PQ?平面DCC1D1, …………………………2分
CD1?平面DCC1D1, …………………………3分
所以PQ∥平面DCC1D1. ……………………4分
法二 取AD的中点G,连接PG,GQ,
则有PG∥DD1,GQ∥DC,且PG∩GQ=G, ………1分
所以平面PGQ∥平面DCC1D1. ………………2分
又PQ?平面PGQ,
所以PQ∥平面DCC1D1. ………………………4分(2)求PQ的长;
(3)求证:EF∥平面BB1D1D.法二 取B1C1的中点E1,连接EE1,FE1,
则有FE1∥B1D1,EE1∥BB1,且FE1∩EE1=E1,
所以平面EE1F∥平面BB1D1D.…………10分
又EF?平面EE1F,
所以EF∥平面BB1D1D.…………………12分方法技巧 直线与平面平行,平面与平面平行的判定定理、性质定理,揭示了线线平行、线面平行、面面平行之间的转化关系,具体转化过程如图所示.即时训练2-1:如图所示,平面α∥平面β,△ABC,△A1B1C1分别在平面α,β内,线段AA1,BB1,CC1相交于点O,点O在α,β之间,若AB=2,AC=1,OA∶OA1=
3∶2,且BA⊥AC,则△A1B1C1的面积为 .?2-2:如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?解:如图,设平面D1BQ∩平面ADD1A1=D1M,点M在AA1上,平面D1BQ∩平面BCC1B1=BQ,平面ADD1A1∥平面BCC1B1,由面面平行的性质定理可得BQ∥D1M.
假设平面D1BQ∥平面PAO,由平面D1BQ∩平面ADD1A1=D1M,平面PAO∩平面ADD1A1=AP,可得AP∥D1M,所以BQ∥D1M∥AP.因为P为DD1的中点,所以M为AA1的中点,Q为CC1的中点,故当Q为CC1的中点时,平面D1BQ∥平面PAO.
