高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.3.1直线与平面垂直的判定(34张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.3.1直线与平面垂直的判定(34张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 16:48:41 | ||
图片预览










文档简介
课件34张PPT。2.3 直线、平面垂直的判定及其性质
2.3.1 直线与平面垂直的判定课标要求:1.理解线面垂直的定义和判定定理.2.能运用线面垂直的判定定理证明一些空间位置关系的简单命题.3.能在简单的几何体中计算线面角.自主学习知识探究1.直线与平面垂直的概念
如果直线l与平面α内的 都垂直,就说直线l与平面α互相垂直,记作 ,直线l叫做平面α的 ,平面α叫做直线l的 ,直线与平面垂直时,它们唯一的公共点叫做 .
探究1:(教师备用)若直线a⊥平面α,直线b?α,则a与b互相垂直吗?
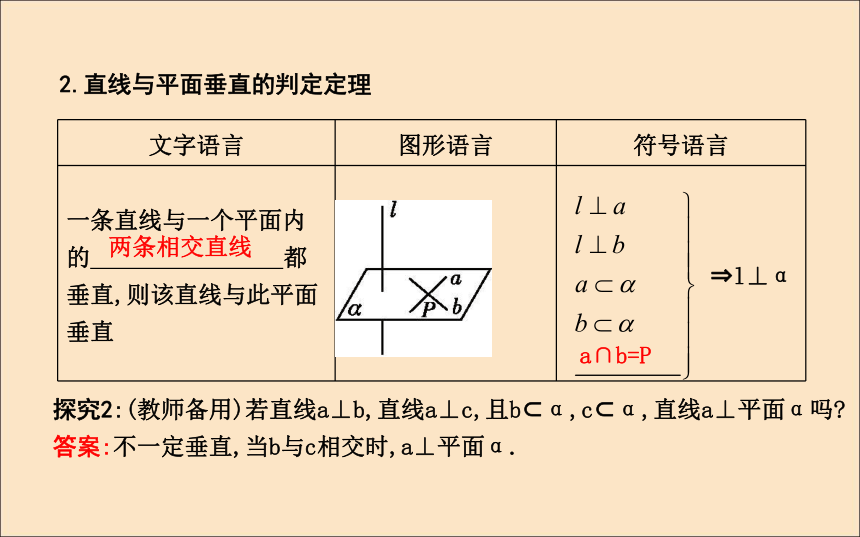
答案:垂直.任意一条直线l⊥α垂线垂面垂足2.直线与平面垂直的判定定理两条相交直线a∩b=P探究2:(教师备用)若直线a⊥b,直线a⊥c,且b?α,c?α,直线a⊥平面α吗?
答案:不一定垂直,当b与c相交时,a⊥平面α.3.直线与平面所成的角
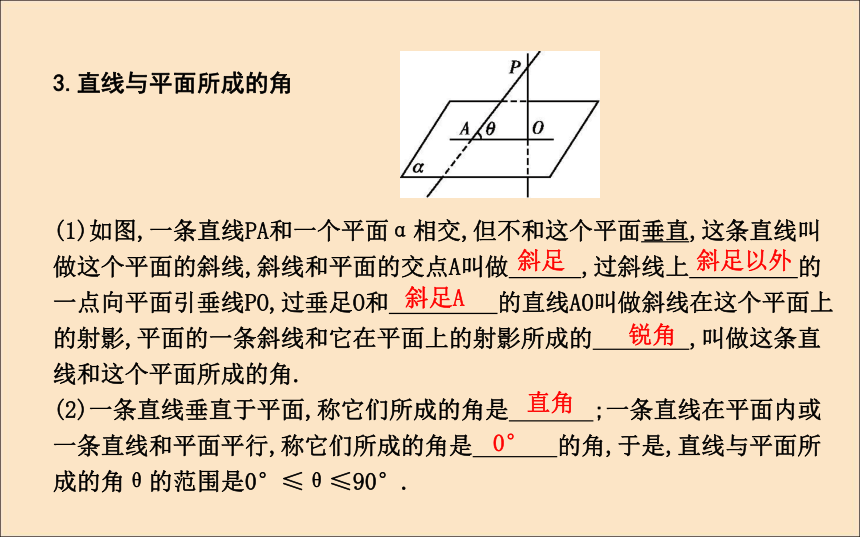
(1)如图,一条直线PA和一个平面α相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A叫做 ,过斜线上 的一点向平面引垂线PO,过垂足O和 的直线AO叫做斜线在这个平面上的射影,平面的一条斜线和它在平面上的射影所成的 ,叫做这条直线和这个平面所成的角.
(2)一条直线垂直于平面,称它们所成的角是 ;一条直线在平面内或一条直线和平面平行,称它们所成的角是 的角,于是,直线与平面所成的角θ的范围是0°≤θ≤90°.斜足斜足以外斜足A锐角直角0°自我检测1.如果一条直线垂直于一个平面内的:①三角形的两边;②梯形的两边;③圆的两条直径;④正六边形的两条边,则能保证该直线与平面垂直的是( )
(A)①③ (B)②
(C)②④ (D)①②④
2.下列条件中,能使直线m⊥α的是( )
(A)m⊥b,m⊥c,b?α,c?α
(B)m⊥b,b∥α
(C)m∩b=A,b⊥α
(D)m∥b,b⊥αAD3.若三条直线OA,OB,OC两两垂直,则直线OA垂直于( )
(A)平面OAB (B)平面OAC
(C)平面OBC (D)平面ABC
4.若直线a和直线b与平面α所成的角相等,则直线a与直线b的位置关系是( )
(A)平行 (B)相交
(C)异面 (D)不确定CD5.在正方体ABCD-A1B1C1D1中,AC1与底面ABCD所成角的正弦值为 .?题型一线面垂直的概念与定理的理解【例1】 下列说法中正确的个数是( )
①若直线l与平面α内一条直线垂直,则l⊥α;
②若直线l与平面α内两条直线垂直,则l⊥α;
③若直线l与平面α内两条相交直线垂直,则l⊥α;
④若直线l与平面α内任意一条直线垂直,则l⊥α;
⑤若直线l与平面α内无数条直线垂直,则l⊥α.
(A)1 (B)2
(C)3 (D)4课堂探究解析:由直线与平面垂直的判定定理和定义知正确的是③④,故选B.误区警示 线面垂直的判定定理中,直线垂直于平面内的两条相交直线,“相交”两字必不可少,否则,就是换成无数条直线,这条直线也不一定与平面垂直.即时训练1-1:如果一条直线垂直于一个平面内的①三角形的两边;②梯形的两边;③圆的两条直径;④正六边形的两条边.则能保证该直线与平面垂直的是 .?解析:三角形两边必相交,圆的两条直径必相交,梯形的两边有可能是平行的一组对边,正六边形的两边也可能是一组平行对边.故由线面垂直的判定定理知,能保证该直线与平面垂直的是①③.
答案:①③1-2:下列命题中,正确命题的序号是 .?
①如果直线l与平面α内的无数条直线垂直,那么l⊥α;②如果直线l与平面α内的两条直线垂直,那么l⊥α;③若l不垂直于α,则在α内没有与l垂直的直线;④过一点和已知平面垂直的直线有且只有一条;⑤若a∥α,b⊥α,则a⊥b;⑥若a∥b,a⊥α,则b⊥α.解析:根据线面垂直的定义,当直线l与平面α内的任意一条直线垂直时,l⊥α,如果α内的无数条直线互相平行,l与α不一定垂直,故①不正确;根据直线与平面垂直的判定定理可知,如果平面α内的两条直线不相交时,l与α不一定垂直,故②不正确;当l与α不垂直时,l可能与α内的无数条互相平行的直线垂直,故③不正确;由于过一点有且只有一条直线与已知平面垂直.故④正确;⑤,⑥显然正确.
答案:④⑤⑥题型二直线与平面垂直的判定【例2】 (12分)在三棱锥P-ABC中,H为△ABC的垂心,AP⊥BC,PC⊥AB,求证:PH⊥平面ABC.所以AH⊥BC,……………………2分
又AP⊥BC,AH∩AP=A,
所以BC⊥平面AHP, ……………4分
又PH?平面AHP,
所以PH⊥BC. ……………………6分
同理可证PH⊥AB, ………………8分
又AB∩BC=B,
所以PH⊥平面ABC. ……………12分变式探究:在三棱锥P-ABC中,H为△ABC的垂心,且PH⊥平面ABC,求证:AB⊥PC,BC⊥AP.证明:如图,连接AH,因为H为△ABC的垂心,
所以AH⊥BC,又PH⊥平面ABC,
所以PH⊥BC,又PH∩AH=H,
所以BC⊥平面PAH,
所以BC⊥AP,同理可证:AB⊥PC.方法技巧 利用直线与平面垂直的判定定理证明线面垂直的关键是在这个平面内找到两条相交直线,证明它们都和这条直线垂直.即时训练2-1:如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明:EO∥平面PAD;证明:(1)连接AC,因为点O是底面正方形ABCD的中心,
所以点O是AC的中点,又因为E是PC的中点,所以在△PAC中,EO是中位线,所以PA∥EO.
因为EO?平面PAD,PA?平面PAD,所以EO∥平面PAD.(2)证明:DE⊥平面PBC.证明:(2)因为PD⊥平面ABCD,BC?平面ABCD,所以PD⊥BC,
因为底面ABCD是正方形,有BC⊥DC,
所以BC⊥平面PDC.
而DE?平面PDC,所以BC⊥DE.
因为PD=DC,可知△PDC是等腰直角三角形,
而DE是斜边PC的中线,所以DE⊥PC.
又BC,PC?平面PBC,且BC∩PC=C,
所以DE⊥平面PBC.2-2:如图,Rt△ABC所在平面外一点S,且SA=SB=SC.点D为斜边AC的中点.
(1)求证:SD⊥平面ABC;证明:(1)如图,取AB中点E,连接SE,DE,
在Rt△ABC中,D,E分别为AC,AB的中点,
所以DE∥BC,且DE⊥AB.
在△SAB中,因为SA=SB,
所以SE⊥AB.又SE∩DE=E,
所以AB⊥平面SDE.
因为SD?平面SDE,所以AB⊥SD.
在△SAC中,因为SA=SC,D为AC的中点,
所以SD⊥AC.
因为SD⊥AC,SD⊥AB,AC∩AB=A,
所以SD⊥平面ABC.(2)若AB=BC,求证:BD⊥平面SAC.证明:(2)因为AB=BC,D为斜边AC的中点,
所以BD⊥AC.由(1)可知,SD⊥平面ABC.
而BD?平面ABC,所以SD⊥BD.
因为SD⊥BD,BD⊥AC,SD∩AC=D,
所以BD⊥平面SAC.题型三直线与平面所成的角(1)证明:如图,连接A1B.在△A1BC中,因为E和F分别是BC和A1C的中点,
所以EF∥BA1.又因为EF?平面A1B1BA,所以EF∥平面A1B1BA.(2)求证:直线AE⊥平面BCB1;(2)证明:因为AB=AC,E为BC的中点,所以AE⊥BC.因为AA1⊥平面ABC,BB1∥AA1,所以BB1⊥平面ABC,从而BB1⊥AE.又因为BC∩BB1=B,所以AE⊥平面BCB1.(3)求直线A1B1与平面BCB1所成角的大小.方法技巧 求平面的斜线与平面所成的角的一般步骤
(1)确定斜线与平面的交点(斜足);(2)通过斜线上除斜足以外的某一点作平面的垂线,连接垂足和斜足即为斜线在平面上的射影,则斜线和射影所成的锐角即为所求的角;(3)求解由斜线、垂线、射影构成的直角三角形.即时训练3-1:已知正三棱锥S-ABC的所有棱长都相等,则SA与平面ABC所成角的余弦值为 .?3-2:(2015·浙江卷)如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.
(1)证明:A1D⊥平面A1BC;(1)证明:设E为BC的中点,连接A1E,AE.由题意得A1E⊥平面ABC,所以A1E⊥AE.
因为AB=AC,所以AE⊥BC.
故AE⊥平面A1BC.
连接DE,由D,E分别为B1C1,BC的中点,得DE∥B1B且DE=B1B,
从而DE∥A1A且DE=A1A,
所以AA1DE为平行四边形.
于是A1D∥AE.
又因为AE⊥平面A1BC,所以A1D⊥平面A1BC.(2)求直线A1B和平面BB1C1C所成的角的正弦值.(2)解:作A1F⊥DE,垂足为F,连接BF.
因为A1E⊥平面ABC,
所以BC⊥A1E.
因为BC⊥AE,
所以BC⊥平面AA1DE.
所以BC⊥A1F,
所以A1F⊥平面BB1C1C.
所以∠A1BF为直线A1B和平面BB1C1C所成的角.
2.3.1 直线与平面垂直的判定课标要求:1.理解线面垂直的定义和判定定理.2.能运用线面垂直的判定定理证明一些空间位置关系的简单命题.3.能在简单的几何体中计算线面角.自主学习知识探究1.直线与平面垂直的概念
如果直线l与平面α内的 都垂直,就说直线l与平面α互相垂直,记作 ,直线l叫做平面α的 ,平面α叫做直线l的 ,直线与平面垂直时,它们唯一的公共点叫做 .
探究1:(教师备用)若直线a⊥平面α,直线b?α,则a与b互相垂直吗?
答案:垂直.任意一条直线l⊥α垂线垂面垂足2.直线与平面垂直的判定定理两条相交直线a∩b=P探究2:(教师备用)若直线a⊥b,直线a⊥c,且b?α,c?α,直线a⊥平面α吗?
答案:不一定垂直,当b与c相交时,a⊥平面α.3.直线与平面所成的角
(1)如图,一条直线PA和一个平面α相交,但不和这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A叫做 ,过斜线上 的一点向平面引垂线PO,过垂足O和 的直线AO叫做斜线在这个平面上的射影,平面的一条斜线和它在平面上的射影所成的 ,叫做这条直线和这个平面所成的角.
(2)一条直线垂直于平面,称它们所成的角是 ;一条直线在平面内或一条直线和平面平行,称它们所成的角是 的角,于是,直线与平面所成的角θ的范围是0°≤θ≤90°.斜足斜足以外斜足A锐角直角0°自我检测1.如果一条直线垂直于一个平面内的:①三角形的两边;②梯形的两边;③圆的两条直径;④正六边形的两条边,则能保证该直线与平面垂直的是( )
(A)①③ (B)②
(C)②④ (D)①②④
2.下列条件中,能使直线m⊥α的是( )
(A)m⊥b,m⊥c,b?α,c?α
(B)m⊥b,b∥α
(C)m∩b=A,b⊥α
(D)m∥b,b⊥αAD3.若三条直线OA,OB,OC两两垂直,则直线OA垂直于( )
(A)平面OAB (B)平面OAC
(C)平面OBC (D)平面ABC
4.若直线a和直线b与平面α所成的角相等,则直线a与直线b的位置关系是( )
(A)平行 (B)相交
(C)异面 (D)不确定CD5.在正方体ABCD-A1B1C1D1中,AC1与底面ABCD所成角的正弦值为 .?题型一线面垂直的概念与定理的理解【例1】 下列说法中正确的个数是( )
①若直线l与平面α内一条直线垂直,则l⊥α;
②若直线l与平面α内两条直线垂直,则l⊥α;
③若直线l与平面α内两条相交直线垂直,则l⊥α;
④若直线l与平面α内任意一条直线垂直,则l⊥α;
⑤若直线l与平面α内无数条直线垂直,则l⊥α.
(A)1 (B)2
(C)3 (D)4课堂探究解析:由直线与平面垂直的判定定理和定义知正确的是③④,故选B.误区警示 线面垂直的判定定理中,直线垂直于平面内的两条相交直线,“相交”两字必不可少,否则,就是换成无数条直线,这条直线也不一定与平面垂直.即时训练1-1:如果一条直线垂直于一个平面内的①三角形的两边;②梯形的两边;③圆的两条直径;④正六边形的两条边.则能保证该直线与平面垂直的是 .?解析:三角形两边必相交,圆的两条直径必相交,梯形的两边有可能是平行的一组对边,正六边形的两边也可能是一组平行对边.故由线面垂直的判定定理知,能保证该直线与平面垂直的是①③.
答案:①③1-2:下列命题中,正确命题的序号是 .?
①如果直线l与平面α内的无数条直线垂直,那么l⊥α;②如果直线l与平面α内的两条直线垂直,那么l⊥α;③若l不垂直于α,则在α内没有与l垂直的直线;④过一点和已知平面垂直的直线有且只有一条;⑤若a∥α,b⊥α,则a⊥b;⑥若a∥b,a⊥α,则b⊥α.解析:根据线面垂直的定义,当直线l与平面α内的任意一条直线垂直时,l⊥α,如果α内的无数条直线互相平行,l与α不一定垂直,故①不正确;根据直线与平面垂直的判定定理可知,如果平面α内的两条直线不相交时,l与α不一定垂直,故②不正确;当l与α不垂直时,l可能与α内的无数条互相平行的直线垂直,故③不正确;由于过一点有且只有一条直线与已知平面垂直.故④正确;⑤,⑥显然正确.
答案:④⑤⑥题型二直线与平面垂直的判定【例2】 (12分)在三棱锥P-ABC中,H为△ABC的垂心,AP⊥BC,PC⊥AB,求证:PH⊥平面ABC.所以AH⊥BC,……………………2分
又AP⊥BC,AH∩AP=A,
所以BC⊥平面AHP, ……………4分
又PH?平面AHP,
所以PH⊥BC. ……………………6分
同理可证PH⊥AB, ………………8分
又AB∩BC=B,
所以PH⊥平面ABC. ……………12分变式探究:在三棱锥P-ABC中,H为△ABC的垂心,且PH⊥平面ABC,求证:AB⊥PC,BC⊥AP.证明:如图,连接AH,因为H为△ABC的垂心,
所以AH⊥BC,又PH⊥平面ABC,
所以PH⊥BC,又PH∩AH=H,
所以BC⊥平面PAH,
所以BC⊥AP,同理可证:AB⊥PC.方法技巧 利用直线与平面垂直的判定定理证明线面垂直的关键是在这个平面内找到两条相交直线,证明它们都和这条直线垂直.即时训练2-1:如图,四棱锥P-ABCD中,O是底面正方形ABCD 的中心,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(1)证明:EO∥平面PAD;证明:(1)连接AC,因为点O是底面正方形ABCD的中心,
所以点O是AC的中点,又因为E是PC的中点,所以在△PAC中,EO是中位线,所以PA∥EO.
因为EO?平面PAD,PA?平面PAD,所以EO∥平面PAD.(2)证明:DE⊥平面PBC.证明:(2)因为PD⊥平面ABCD,BC?平面ABCD,所以PD⊥BC,
因为底面ABCD是正方形,有BC⊥DC,
所以BC⊥平面PDC.
而DE?平面PDC,所以BC⊥DE.
因为PD=DC,可知△PDC是等腰直角三角形,
而DE是斜边PC的中线,所以DE⊥PC.
又BC,PC?平面PBC,且BC∩PC=C,
所以DE⊥平面PBC.2-2:如图,Rt△ABC所在平面外一点S,且SA=SB=SC.点D为斜边AC的中点.
(1)求证:SD⊥平面ABC;证明:(1)如图,取AB中点E,连接SE,DE,
在Rt△ABC中,D,E分别为AC,AB的中点,
所以DE∥BC,且DE⊥AB.
在△SAB中,因为SA=SB,
所以SE⊥AB.又SE∩DE=E,
所以AB⊥平面SDE.
因为SD?平面SDE,所以AB⊥SD.
在△SAC中,因为SA=SC,D为AC的中点,
所以SD⊥AC.
因为SD⊥AC,SD⊥AB,AC∩AB=A,
所以SD⊥平面ABC.(2)若AB=BC,求证:BD⊥平面SAC.证明:(2)因为AB=BC,D为斜边AC的中点,
所以BD⊥AC.由(1)可知,SD⊥平面ABC.
而BD?平面ABC,所以SD⊥BD.
因为SD⊥BD,BD⊥AC,SD∩AC=D,
所以BD⊥平面SAC.题型三直线与平面所成的角(1)证明:如图,连接A1B.在△A1BC中,因为E和F分别是BC和A1C的中点,
所以EF∥BA1.又因为EF?平面A1B1BA,所以EF∥平面A1B1BA.(2)求证:直线AE⊥平面BCB1;(2)证明:因为AB=AC,E为BC的中点,所以AE⊥BC.因为AA1⊥平面ABC,BB1∥AA1,所以BB1⊥平面ABC,从而BB1⊥AE.又因为BC∩BB1=B,所以AE⊥平面BCB1.(3)求直线A1B1与平面BCB1所成角的大小.方法技巧 求平面的斜线与平面所成的角的一般步骤
(1)确定斜线与平面的交点(斜足);(2)通过斜线上除斜足以外的某一点作平面的垂线,连接垂足和斜足即为斜线在平面上的射影,则斜线和射影所成的锐角即为所求的角;(3)求解由斜线、垂线、射影构成的直角三角形.即时训练3-1:已知正三棱锥S-ABC的所有棱长都相等,则SA与平面ABC所成角的余弦值为 .?3-2:(2015·浙江卷)如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.
(1)证明:A1D⊥平面A1BC;(1)证明:设E为BC的中点,连接A1E,AE.由题意得A1E⊥平面ABC,所以A1E⊥AE.
因为AB=AC,所以AE⊥BC.
故AE⊥平面A1BC.
连接DE,由D,E分别为B1C1,BC的中点,得DE∥B1B且DE=B1B,
从而DE∥A1A且DE=A1A,
所以AA1DE为平行四边形.
于是A1D∥AE.
又因为AE⊥平面A1BC,所以A1D⊥平面A1BC.(2)求直线A1B和平面BB1C1C所成的角的正弦值.(2)解:作A1F⊥DE,垂足为F,连接BF.
因为A1E⊥平面ABC,
所以BC⊥A1E.
因为BC⊥AE,
所以BC⊥平面AA1DE.
所以BC⊥A1F,
所以A1F⊥平面BB1C1C.
所以∠A1BF为直线A1B和平面BB1C1C所成的角.
