高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.3.2平面与平面垂直的判定(31张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.3.2平面与平面垂直的判定(31张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 16:53:46 | ||
图片预览







文档简介
课件31张PPT。2.3.2 平面与平面垂直的判定课标要求:1.了解二面角及其平面角的定义,并会求简单二面角的大小.2.理解两个平面互相垂直的定义.3.理解两个平面垂直的判定定理,并能用定理判定面面垂直.自主学习知识探究1.二面角
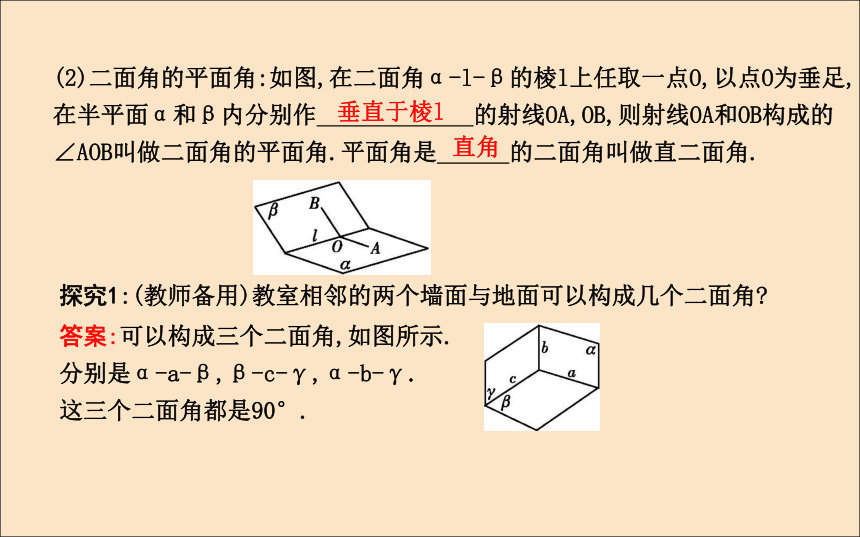
(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫二面角的 ,这两个半平面叫二面角的 .图中的二面角可记作:二面角α-AB-β或α-l-β或P-AB-Q.棱面(2)二面角的平面角:如图,在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作 的射线OA,OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.平面角是 的二面角叫做直二面角.垂直于棱l直角探究1:(教师备用)教室相邻的两个墙面与地面可以构成几个二面角?答案:可以构成三个二面角,如图所示.
分别是α-a-β,β-c-γ,α-b-γ.
这三个二面角都是90°.2.平面与平面垂直
(1)定义:一般地,两个平面相交,如果它们所成的二面角是 ,就说这两个平面互相垂直.平面α与β垂直,记作 .直二面角α⊥β (2)判定定理另一个平面的垂线 探究2:(教师备用)过平面外一点,可以作多少个与已知平面垂直的平面?答案:无数多个.过平面外一点可以作平面的一条垂线,过此垂线可以作出无数个平面,这些平面都与已知平面垂直.自我检测(教师备用)1.下列结论:(1)两个相交平面组成的图形叫做二面角;
(2)异面直线a,b分别和一个二面角的两个半平面垂直,则a,b所成的角与这个二面角的平面角相等或互补.
(3)二面角的平面角是从棱上一点出发,分别在两个半平面内作射线所成角的最小角;
(4)二面角的大小与其平面角的顶点在棱上的位置没有关系.
其中正确的是( )
(A)①③ (B)②④ (C)③④ (D)①②B2.用a,b,c表示空间三条不同的直线,α,γ表示平面,给出下列命题:①若a⊥b,b⊥c,则a∥c;②若a∥b,b∥c,则a∥c;③若a∥γ,b∥γ,则a∥b;④若a⊥γ,a?α,则α⊥γ.其中正确命题的序号是( )
(A)①② (B)②③ (C)①④ (D)②④
3.在正方体ABCD-A1B1C1D1的六个面中,与面ABCD垂直的平面有( )
(A)1个 (B)2个 (C)3个 (D)4个D D 4.三棱锥P-ABC的两侧面PAB,PBC都是边长为2的正三角形,AC= ,则二面角A-PB-C的大小为 .?答案:60°5.如图,P是边长为2 的正方形ABCD所在平面外一点,PA⊥AB,PA⊥BC,且PC=5,则二面角P-BD-A的余弦值为 .?答案:题型一 求二面角【例1-1】 如图所示,在正方体ABCD-A′B′C′D′中:课堂探究(1)求二面角D′-AB-D的大小;解:(1)在正方体ABCD-A′B′C′D′中,AB⊥平面ADD′A′,所以AB⊥AD′,
AB⊥AD,因此∠D′AD为二面角D′-AB-D的平面角,在Rt△D′DA中,
∠D′AD=45°.
所以二面角D′-AB-D的大小为45°.(2)若M是C′D′的中点,求二面角M-AB-D的大小.解:(2)因为M是C′D′的中点,所以MA=MB,取AB的中点N,连接MN,则MN⊥AB.取CD的中点H,连接HN,则HN⊥AB.从而∠MNH是二面角M-AB-D的平面角.
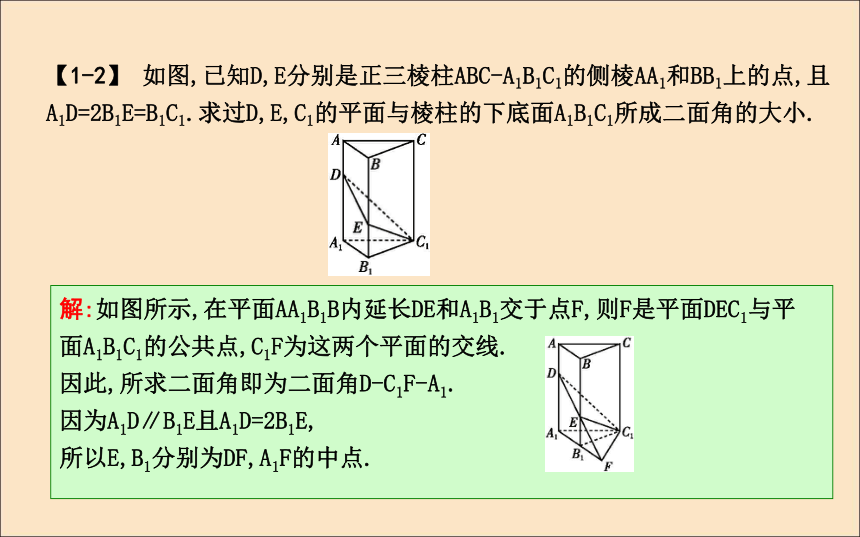
∠MNH=45°.所以二面角M-AB-D的大小为45°.【1-2】 如图,已知D,E分别是正三棱柱ABC-A1B1C1的侧棱AA1和BB1上的点,且A1D=2B1E=B1C1.求过D,E,C1的平面与棱柱的下底面A1B1C1所成二面角的大小.解:如图所示,在平面AA1B1B内延长DE和A1B1交于点F,则F是平面DEC1与平面A1B1C1的公共点,C1F为这两个平面的交线.
因此,所求二面角即为二面角D-C1F-A1.
因为A1D∥B1E且A1D=2B1E,
所以E,B1分别为DF,A1F的中点.因为A1B1=B1C1=B1F,
所以FC1⊥A1C1.
因为CC1⊥平面A1B1C1,FC1?平面A1B1C1,
所以CC1⊥FC1.
又A1C1,CC1为平面AA1C1C内的两条相交直线,
所以FC1⊥平面AA1C1C.
因为DC1?平面AA1C1C,
所以FC1⊥DC1.
所以∠DC1A1是二面角D-C1F-A1的平面角.
由A1D=B1C1知A1D=A1C1,则∠DC1A1=45°.
故所求二面角的大小为45°.方法技巧 (1)二面角的平面角满足:①顶点在二面角的棱上;②两边分别在二面角的两个半平面内;③两边分别与二面角的棱垂直.
(2)二面角的平面角θ是两条射线所成的角,因此二面角不一定是锐角,其范围为0°≤θ≤180°.即时训练1-1:正方体ABCD-A1B1C1D1中,二面角C1-AB-C的平面角等于 .?解析:因为ABCD-A1B1C1D1为正方体,所以AB⊥平面BCC1B1,
因为BC?平面BCC1B1,BC1?平面BCC1B1,
所以AB⊥BC,AB⊥BC1,
所以∠CBC1为二面角C1-AB-C的平面角,
又ABCD-A1B1C1D1为正方体.所以∠C1BC=45°.答案:45°1-2:在四棱锥P-ABCD中,底面是边长为a的正方形,PD⊥平面ABCD,PD=a.
(1)求证:AC⊥平面PBD;(1)证明:因为四边形ABCD为正方形,
所以AC⊥BD,
又PD⊥平面ABCD,
所以AC⊥PD,
又PD∩BD=D,
所以AC⊥平面PBD.(2)求二面角P-BC-D的平面角;(2)解:因为四边形ABCD为正方形,所以BC⊥CD,
又PD⊥平面ABCD,所以BC⊥PD.
又CD∩PD=D,所以BC⊥平面PCD,
所以BC⊥PC,
所以∠PCD为二面角P-BC-D的平面角,
在Rt△PCD中,因为PD=DC=a,
所以∠PCD=45°,
即二面角P-BC-D的平面角为45°.(3)求二面角P-AC-D的平面角的正切值.题型二 平面与平面垂直的判定【例2】 (1)如图(1)在四面体ABCD中,BD= a,AB=AD=CB=CD=AC=a.
求证:平面ABD⊥平面BCD;(2)如图(2),在正三棱柱ABC-A1B1C1中,D为BC的中点,点E在AC上,且DE⊥A1E.
①求证:平面A1AD⊥平面BCC1B1;
②求证:平面A1DE⊥平面ACC1A1.证明:(2)①因为三棱柱ABC-A1B1C1为正三棱柱,
所以BB1⊥平面ABC,又AD?平面ABC,
所以AD⊥BB1,又D为BC的中点,所以AD⊥BC,又BC∩BB1=B,
所以AD⊥平面BCC1B1.又AD?平面ADA1,所以平面A1AD⊥平面BCC1B1.
②因为三棱柱ABC-A1B1C1为正三棱柱,所以AA1⊥平面ABC,又DE?平面ABC,
所以AA1⊥DE,又DE⊥A1E,A1E∩AA1=A1,所以DE⊥平面ACC1A1,
又DE?平面A1DE,所以平面A1DE⊥平面ACC1A1.变式探究:若本例中(2)改为在正三棱柱ABC-A1B1C1中,F为A1C1的中点,求证:平面AB1F⊥平面ACC1A1.证明:因为三棱柱ABC-A1B1C1为正三棱柱,
所以AA1⊥平面A1B1C1,
又FB1?平面A1B1C1,所以AA1⊥FB1,
又△A1B1C1为等边三角形,
F为A1C1的中点,所以B1F⊥A1C1,
又A1C1∩AA1=A1,
所以B1F⊥平面ACC1A1,又B1F?平面AB1F,所以平面AB1F⊥平面ACC1A1.方法技巧 判定两平面垂直的常用方法:(1)定义法:即说明两个平面所成的二面角是直二面角;(2)判定定理法:其关键是在其中一个平面内寻找一直线与另一个平面垂直,即把问题转化为“线面垂直”;(3)性质法:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.即时训练2-1:如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,
E为PC的中点.
求证:平面PAC⊥平面BDE.证明:因为四边形ABCD为正方形,
所以BD⊥AC,又PO⊥平面ABCD,所以PO⊥BD,
又AC∩PO=O,AC?平面PAC,PO?平面PAC,
所以BD⊥平面PAC,
又BD?平面BDE,
所以平面BDE⊥平面PAC.2-2:如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.证明:平面ABM⊥平面A1B1M.2-3:如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,
E,F分别是A1C1,BC的中点.(1)求证:平面ABE⊥平面B1BCC1;(1)证明:因为在三棱柱ABC-A1B1C1中,侧棱垂直于底面
所以BB1⊥AB,
又因为AB⊥BC,BB1∩BC=B,
所以AB⊥平面B1BCC1,
因为AB?平面ABE.
所以平面ABE⊥平面B1BCC1.(2)求证:C1F∥平面ABE;(2)证明:取AB的中点G,连接EG,FG.
因为E,F分别是A1C1,BC的中点,
所以FG∥AC,且FG= AC.
因为AC∥A1C1,且AC=A1C1,
所以FG∥EC1,且FG=EC1.
所以四边形FGEC1为平行四边形,
所以C1F∥EG.
又因为EG?平面ABE,C1F?平面ABE,
所以C1F∥平面ABE.(3)求三棱锥E-ABC的体积.题型三 线面垂直、面面垂直的综合问题【例3】 如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,BC=2 .
(1)求证:平面PAB⊥平面ABC;(2)E为BA的延长线上一点,若二面角P-EC-B的大小为30°,求BE的长.方法技巧 (1)证明垂直关系时要注意利用线面垂直、线线垂直、面面垂直之间的转化.
(2)求二面角的大小的关键是作出二面角的平面角,这就需要紧扣它的三个条件,即这个角的顶点是否在棱上;角的两边是否分别在两个半平面内;这两边是否都与棱垂直.在具体作图时,还要注意掌握一些作二面角的平面角的方法技巧,如:线面的垂直,图形的对称性,与棱垂直的面等.即时训练3-1:如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
(1)证明:平面AEC⊥平面BED;(1)证明:因为四边形ABCD为菱形,所以AC⊥BD.
又BE⊥平面ABCD,所以BE⊥AC,又BD∩BE=B,
所以AC⊥平面BED,又AC?平面AEC,
所以平面AEC⊥平面BED.(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为 ,求该三棱锥的侧面积.
(1)定义:从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫二面角的 ,这两个半平面叫二面角的 .图中的二面角可记作:二面角α-AB-β或α-l-β或P-AB-Q.棱面(2)二面角的平面角:如图,在二面角α-l-β的棱l上任取一点O,以点O为垂足,在半平面α和β内分别作 的射线OA,OB,则射线OA和OB构成的∠AOB叫做二面角的平面角.平面角是 的二面角叫做直二面角.垂直于棱l直角探究1:(教师备用)教室相邻的两个墙面与地面可以构成几个二面角?答案:可以构成三个二面角,如图所示.
分别是α-a-β,β-c-γ,α-b-γ.
这三个二面角都是90°.2.平面与平面垂直
(1)定义:一般地,两个平面相交,如果它们所成的二面角是 ,就说这两个平面互相垂直.平面α与β垂直,记作 .直二面角α⊥β (2)判定定理另一个平面的垂线 探究2:(教师备用)过平面外一点,可以作多少个与已知平面垂直的平面?答案:无数多个.过平面外一点可以作平面的一条垂线,过此垂线可以作出无数个平面,这些平面都与已知平面垂直.自我检测(教师备用)1.下列结论:(1)两个相交平面组成的图形叫做二面角;
(2)异面直线a,b分别和一个二面角的两个半平面垂直,则a,b所成的角与这个二面角的平面角相等或互补.
(3)二面角的平面角是从棱上一点出发,分别在两个半平面内作射线所成角的最小角;
(4)二面角的大小与其平面角的顶点在棱上的位置没有关系.
其中正确的是( )
(A)①③ (B)②④ (C)③④ (D)①②B2.用a,b,c表示空间三条不同的直线,α,γ表示平面,给出下列命题:①若a⊥b,b⊥c,则a∥c;②若a∥b,b∥c,则a∥c;③若a∥γ,b∥γ,则a∥b;④若a⊥γ,a?α,则α⊥γ.其中正确命题的序号是( )
(A)①② (B)②③ (C)①④ (D)②④
3.在正方体ABCD-A1B1C1D1的六个面中,与面ABCD垂直的平面有( )
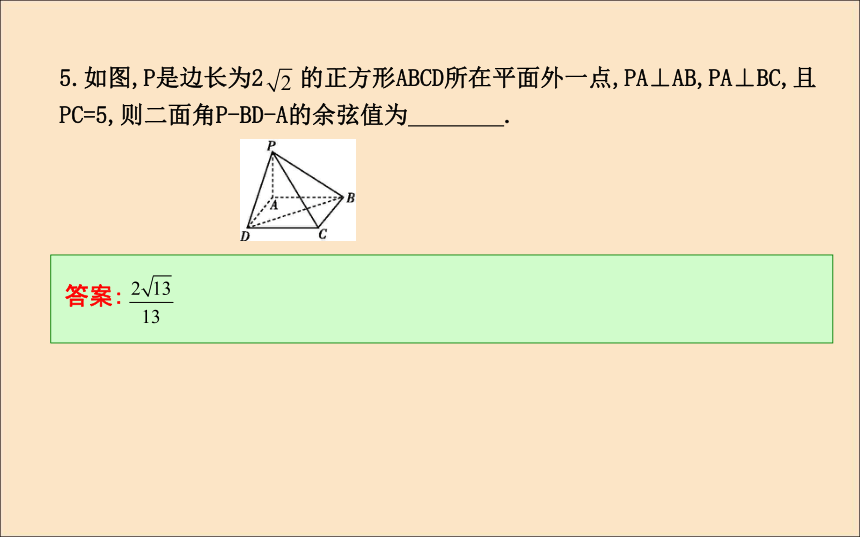
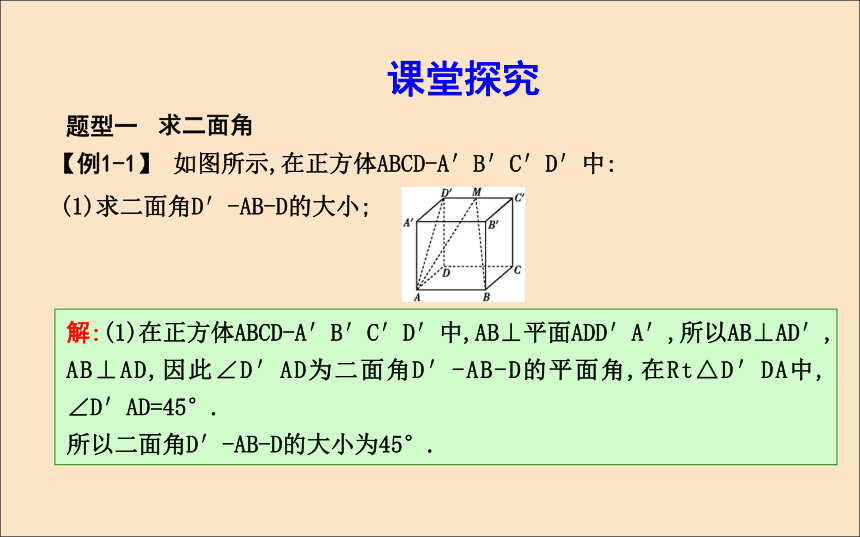
(A)1个 (B)2个 (C)3个 (D)4个D D 4.三棱锥P-ABC的两侧面PAB,PBC都是边长为2的正三角形,AC= ,则二面角A-PB-C的大小为 .?答案:60°5.如图,P是边长为2 的正方形ABCD所在平面外一点,PA⊥AB,PA⊥BC,且PC=5,则二面角P-BD-A的余弦值为 .?答案:题型一 求二面角【例1-1】 如图所示,在正方体ABCD-A′B′C′D′中:课堂探究(1)求二面角D′-AB-D的大小;解:(1)在正方体ABCD-A′B′C′D′中,AB⊥平面ADD′A′,所以AB⊥AD′,
AB⊥AD,因此∠D′AD为二面角D′-AB-D的平面角,在Rt△D′DA中,
∠D′AD=45°.
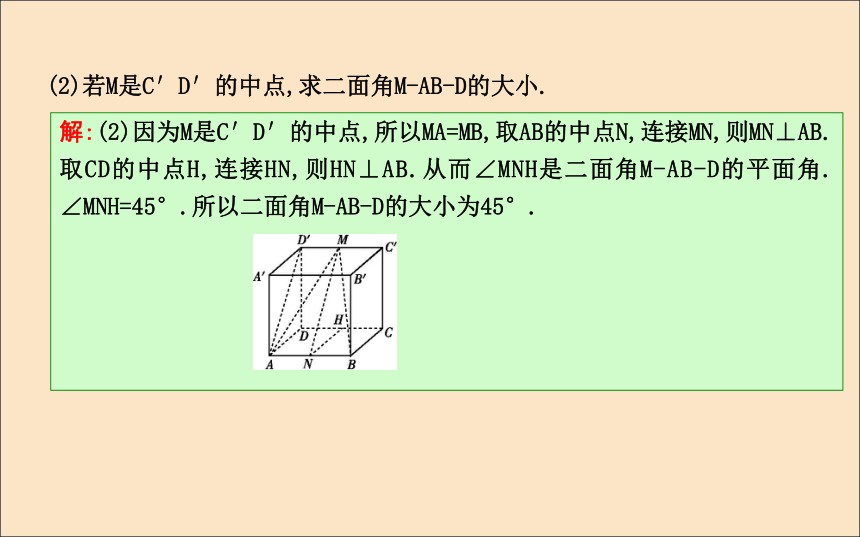
所以二面角D′-AB-D的大小为45°.(2)若M是C′D′的中点,求二面角M-AB-D的大小.解:(2)因为M是C′D′的中点,所以MA=MB,取AB的中点N,连接MN,则MN⊥AB.取CD的中点H,连接HN,则HN⊥AB.从而∠MNH是二面角M-AB-D的平面角.
∠MNH=45°.所以二面角M-AB-D的大小为45°.【1-2】 如图,已知D,E分别是正三棱柱ABC-A1B1C1的侧棱AA1和BB1上的点,且A1D=2B1E=B1C1.求过D,E,C1的平面与棱柱的下底面A1B1C1所成二面角的大小.解:如图所示,在平面AA1B1B内延长DE和A1B1交于点F,则F是平面DEC1与平面A1B1C1的公共点,C1F为这两个平面的交线.
因此,所求二面角即为二面角D-C1F-A1.
因为A1D∥B1E且A1D=2B1E,
所以E,B1分别为DF,A1F的中点.因为A1B1=B1C1=B1F,
所以FC1⊥A1C1.
因为CC1⊥平面A1B1C1,FC1?平面A1B1C1,
所以CC1⊥FC1.
又A1C1,CC1为平面AA1C1C内的两条相交直线,
所以FC1⊥平面AA1C1C.
因为DC1?平面AA1C1C,
所以FC1⊥DC1.
所以∠DC1A1是二面角D-C1F-A1的平面角.
由A1D=B1C1知A1D=A1C1,则∠DC1A1=45°.
故所求二面角的大小为45°.方法技巧 (1)二面角的平面角满足:①顶点在二面角的棱上;②两边分别在二面角的两个半平面内;③两边分别与二面角的棱垂直.
(2)二面角的平面角θ是两条射线所成的角,因此二面角不一定是锐角,其范围为0°≤θ≤180°.即时训练1-1:正方体ABCD-A1B1C1D1中,二面角C1-AB-C的平面角等于 .?解析:因为ABCD-A1B1C1D1为正方体,所以AB⊥平面BCC1B1,
因为BC?平面BCC1B1,BC1?平面BCC1B1,
所以AB⊥BC,AB⊥BC1,
所以∠CBC1为二面角C1-AB-C的平面角,
又ABCD-A1B1C1D1为正方体.所以∠C1BC=45°.答案:45°1-2:在四棱锥P-ABCD中,底面是边长为a的正方形,PD⊥平面ABCD,PD=a.
(1)求证:AC⊥平面PBD;(1)证明:因为四边形ABCD为正方形,
所以AC⊥BD,
又PD⊥平面ABCD,
所以AC⊥PD,
又PD∩BD=D,
所以AC⊥平面PBD.(2)求二面角P-BC-D的平面角;(2)解:因为四边形ABCD为正方形,所以BC⊥CD,
又PD⊥平面ABCD,所以BC⊥PD.
又CD∩PD=D,所以BC⊥平面PCD,
所以BC⊥PC,
所以∠PCD为二面角P-BC-D的平面角,
在Rt△PCD中,因为PD=DC=a,
所以∠PCD=45°,
即二面角P-BC-D的平面角为45°.(3)求二面角P-AC-D的平面角的正切值.题型二 平面与平面垂直的判定【例2】 (1)如图(1)在四面体ABCD中,BD= a,AB=AD=CB=CD=AC=a.
求证:平面ABD⊥平面BCD;(2)如图(2),在正三棱柱ABC-A1B1C1中,D为BC的中点,点E在AC上,且DE⊥A1E.
①求证:平面A1AD⊥平面BCC1B1;
②求证:平面A1DE⊥平面ACC1A1.证明:(2)①因为三棱柱ABC-A1B1C1为正三棱柱,
所以BB1⊥平面ABC,又AD?平面ABC,
所以AD⊥BB1,又D为BC的中点,所以AD⊥BC,又BC∩BB1=B,
所以AD⊥平面BCC1B1.又AD?平面ADA1,所以平面A1AD⊥平面BCC1B1.
②因为三棱柱ABC-A1B1C1为正三棱柱,所以AA1⊥平面ABC,又DE?平面ABC,
所以AA1⊥DE,又DE⊥A1E,A1E∩AA1=A1,所以DE⊥平面ACC1A1,
又DE?平面A1DE,所以平面A1DE⊥平面ACC1A1.变式探究:若本例中(2)改为在正三棱柱ABC-A1B1C1中,F为A1C1的中点,求证:平面AB1F⊥平面ACC1A1.证明:因为三棱柱ABC-A1B1C1为正三棱柱,
所以AA1⊥平面A1B1C1,
又FB1?平面A1B1C1,所以AA1⊥FB1,
又△A1B1C1为等边三角形,
F为A1C1的中点,所以B1F⊥A1C1,
又A1C1∩AA1=A1,
所以B1F⊥平面ACC1A1,又B1F?平面AB1F,所以平面AB1F⊥平面ACC1A1.方法技巧 判定两平面垂直的常用方法:(1)定义法:即说明两个平面所成的二面角是直二面角;(2)判定定理法:其关键是在其中一个平面内寻找一直线与另一个平面垂直,即把问题转化为“线面垂直”;(3)性质法:两个平行平面中的一个垂直于第三个平面,则另一个也垂直于此平面.即时训练2-1:如图,四边形ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,
E为PC的中点.
求证:平面PAC⊥平面BDE.证明:因为四边形ABCD为正方形,
所以BD⊥AC,又PO⊥平面ABCD,所以PO⊥BD,
又AC∩PO=O,AC?平面PAC,PO?平面PAC,
所以BD⊥平面PAC,
又BD?平面BDE,
所以平面BDE⊥平面PAC.2-2:如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.证明:平面ABM⊥平面A1B1M.2-3:如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,
E,F分别是A1C1,BC的中点.(1)求证:平面ABE⊥平面B1BCC1;(1)证明:因为在三棱柱ABC-A1B1C1中,侧棱垂直于底面
所以BB1⊥AB,
又因为AB⊥BC,BB1∩BC=B,
所以AB⊥平面B1BCC1,
因为AB?平面ABE.
所以平面ABE⊥平面B1BCC1.(2)求证:C1F∥平面ABE;(2)证明:取AB的中点G,连接EG,FG.
因为E,F分别是A1C1,BC的中点,
所以FG∥AC,且FG= AC.
因为AC∥A1C1,且AC=A1C1,
所以FG∥EC1,且FG=EC1.
所以四边形FGEC1为平行四边形,
所以C1F∥EG.
又因为EG?平面ABE,C1F?平面ABE,
所以C1F∥平面ABE.(3)求三棱锥E-ABC的体积.题型三 线面垂直、面面垂直的综合问题【例3】 如图,在三棱锥P-ABC中,PA⊥平面PBC,PA=PB=2,PC=4,BC=2 .
(1)求证:平面PAB⊥平面ABC;(2)E为BA的延长线上一点,若二面角P-EC-B的大小为30°,求BE的长.方法技巧 (1)证明垂直关系时要注意利用线面垂直、线线垂直、面面垂直之间的转化.
(2)求二面角的大小的关键是作出二面角的平面角,这就需要紧扣它的三个条件,即这个角的顶点是否在棱上;角的两边是否分别在两个半平面内;这两边是否都与棱垂直.在具体作图时,还要注意掌握一些作二面角的平面角的方法技巧,如:线面的垂直,图形的对称性,与棱垂直的面等.即时训练3-1:如图,四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
(1)证明:平面AEC⊥平面BED;(1)证明:因为四边形ABCD为菱形,所以AC⊥BD.
又BE⊥平面ABCD,所以BE⊥AC,又BD∩BE=B,
所以AC⊥平面BED,又AC?平面AEC,
所以平面AEC⊥平面BED.(2)若∠ABC=120°,AE⊥EC,三棱锥E-ACD的体积为 ,求该三棱锥的侧面积.
