高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.3.3直线与平面垂直的性质2.3.4平面与平面垂直的性质(35张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第二章点、直线、平面之间的位置关系2.3.3直线与平面垂直的性质2.3.4平面与平面垂直的性质(35张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 16:56:24 | ||
图片预览








文档简介
课件35张PPT。2.3.3 直线与平面垂直的性质
2.3.4 平面与平面垂直的性质课标要求:理解直线与平面垂直、平面与平面垂直的性质,并能运用性质定理解决一些简单问题.自主学习知识探究1.直线与平面垂直的性质定理a∥b 探究1:(教师备用)(1)垂直于同一个平面的两条直线一定共面吗?
(2)三角形的两边可以垂直于同一个平面吗?
(3)过一点有几条直线与已知平面垂直?
答案:(1)共面.由线面垂直的性质定理可知这两条直线是平行的,故能确定一个平面.
(2)不可以.若三角形的两边垂直于同一个平面,则这两条边平行,不能构成三角形.
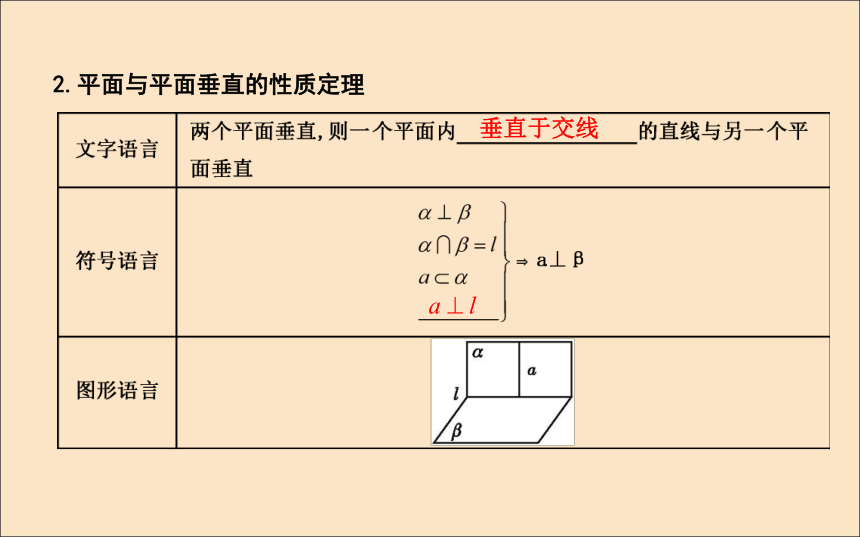
(3)有且仅有一条.假设过一点有两条直线与已知平面垂直,由直线与平面垂直的性质定理可得这两条直线平行,应无公共点,这与过同一点相矛盾,故只有一条直线.2.平面与平面垂直的性质定理垂直于交线 探究2:(教师备用)(1)如果α⊥β,则α内的直线必垂直于β内的无数条直线吗?
(2)如果α⊥β,过β内的任意一点作α与β交线的垂线,则这条直线必垂直于α吗?
答案:(1)正确.若设α∩β=l,a?α,b?β,b⊥l,则a⊥b,故β内与b平行的无数条直线均垂直于α内的任意直线.
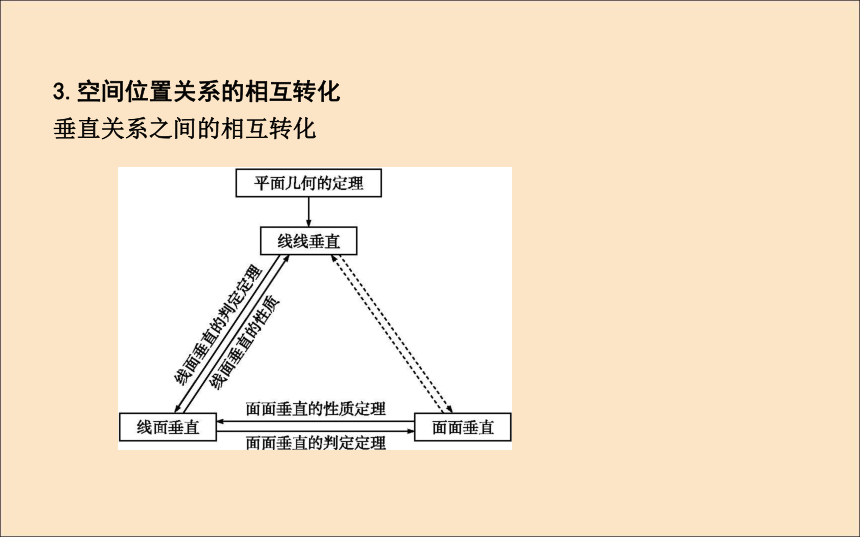
(2)错误.垂直于交线的直线必须在平面β内才与平面α垂直,否则不垂直.3.空间位置关系的相互转化
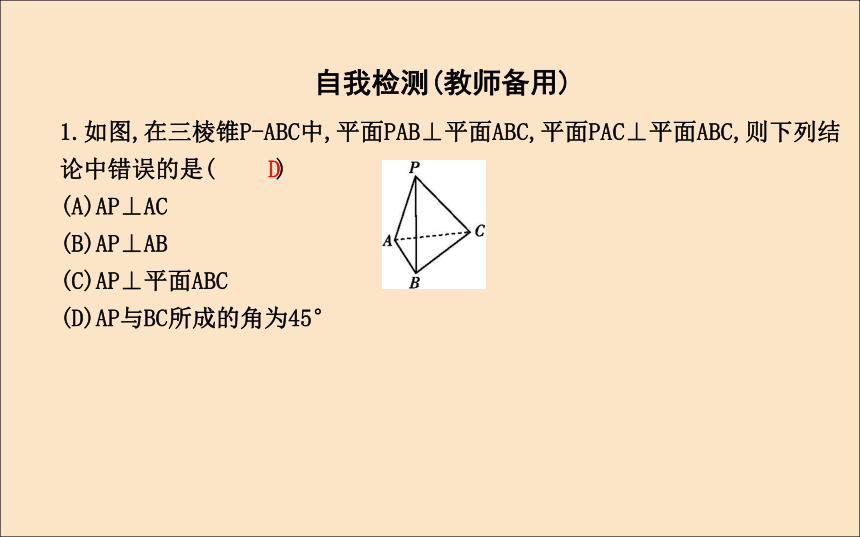
垂直关系之间的相互转化自我检测(教师备用)1.如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,平面PAC⊥平面ABC,则下列结论中错误的是( )
(A)AP⊥AC
(B)AP⊥AB
(C)AP⊥平面ABC
(D)AP与BC所成的角为45°D2.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
(A)若α⊥β,m?α,n?β,则m⊥n
(B)若α∥β,m?α,n?β,则m∥n
(C)若m⊥n,m?α,n?β,则α⊥β
(D)若m⊥α,m∥n,n∥β,则α⊥βD 3.已知m,n是两条不同的直线,α,β是两个不同的平面,且m∥α,n?β,则下列叙述正确的是( )
(A)若α∥β,则m∥n (B)若m∥n,则α∥β
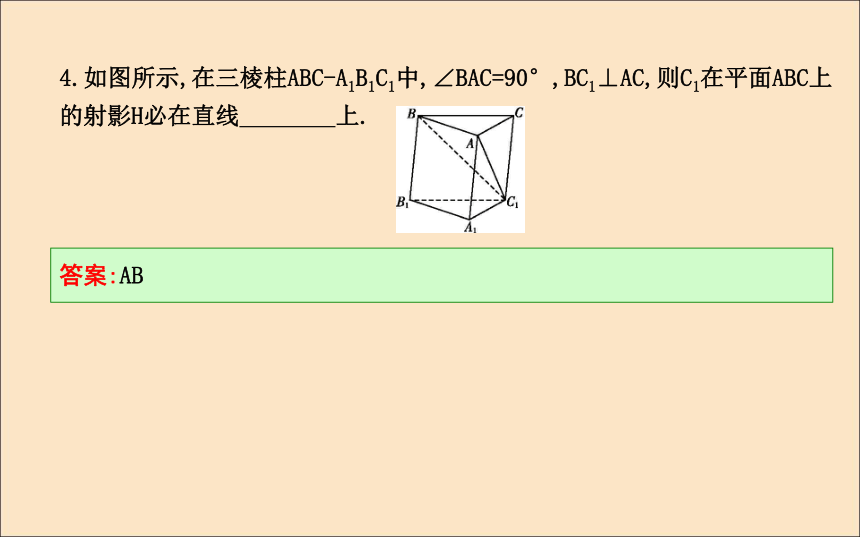
(C)若n⊥α,则m⊥β (D)若m⊥β,则α⊥βD 4.如图所示,在三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在平面ABC上的射影H必在直线 上.?答案:AB5.设α,β是空间两个不同的平面,m,n是平面α及β外的两条不同直线.从“①m⊥n;②α⊥β;③n⊥β;④m⊥α”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题: (用序号表示).?答案:①③④?②(或②③④?①)题型一 直线与平面垂直的性质定理的应用【例1】 (1)已知两条直线m,n,两个平面α,β,给出下面四个命题:
①m∥n,m⊥α?n⊥α;②α∥β,m?α,n?β?m∥n;③m∥n,m∥α?
n∥α;④α∥β,m∥n,m⊥α?n⊥β.
其中正确命题的序号是( )
(A)①③ (B)②④ (C)①④ (D)②③课堂探究(1)解析:由线面垂直的性质定理可知①正确;对于②,当α∥β,m?α,
n?β时,m与n可能平行也可能异面,故②不正确;对于③,当m∥n,m∥α时,n∥α或n?α,故③不正确;对于④,由m∥n,m⊥α,得n⊥α,又α∥β,所以n⊥β,故④正确.故选C.(2)如图所示,在正方体ABCD-A1B1C1D1中,M是AB上的一点,N是A1C的中点,
MN⊥平面A1DC.
求证:①MN∥AD1;(2)证明:①因为ABCD-A1B1C1D1为正方体,
所以AD1⊥A1D.
又因为CD⊥平面ADD1A1,AD1?平面ADD1A1,
所以CD⊥AD1.因为A1D∩CD=D,
所以AD1⊥平面A1DC.
又因为MN⊥平面A1DC,
所以MN∥AD1.②M是AB的中点.方法技巧 证明两条直线平行的方法常见的有:(1)公理4:平行于同一条直线的两条直线平行;(2)线面平行的性质定理:如果一条直线与一个平面平行,那么经过这条直线的任一平面与此平面的交线与该直线平行;(3)面面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行;(4)线面垂直的性质定理:垂直于同一个平面的两条直线平行.即时训练1-1:如图所示,已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于点E,过点E作EF⊥SC交SC于点F.
(1)求证:AF⊥SC;证明:(1)因为SA⊥平面AC,BC?平面AC,所以SA⊥BC,
因为ABCD为矩形,所以AB⊥BC,
又SA∩AB=A,所以BC⊥平面SAB,所以BC⊥AE.
又SB⊥AE,BC∩SB=B,所以AE⊥平面SBC,所以AE⊥SC.
又EF⊥SC,AE∩EF=E,所以SC⊥平面AEF,所以AF⊥SC.(2)若平面AEF交SD于点G.求证:AG⊥SD.证明:(2)因为SA⊥平面AC,所以SA⊥DC,
又AD⊥DC,SA∩AD=A,
所以DC⊥平面SAD.
所以DC⊥AG.
又由(1)有SC⊥平面AEF,AG?平面AEF,
所以SC⊥AG,
又DC∩SC=C,
所以AG⊥平面SDC,所以AG⊥SD.1-2:下列命题:
①垂直于同一条直线的两个平面互相平行;
②垂直于同一个平面的两条直线互相平行;
③一条直线在平面内,另一条直线与这个平面垂直,则这两条直线互相垂直.
其中正确的个数是( )
(A)0 (B)1 (C)2 (D)3解析:①②③均正确.故选D.题型二 平面与平面垂直的性质定理的应用【例2-1】 (12分)如图,P是四边形ABCD所在平面外一点,四边形ABCD是∠DAB=60°,且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD边的中点,求证:BG⊥平面PAD;规范解答:(1)如图所示,连接BD.
因为四边形ABCD是菱形,
且∠DAB=60°,所以△ABD是正三角形,…………………2分
因为G是AD的中点,所以BG⊥AD.…………………………3分
又因为平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD.所以BG⊥平面PAD.……………6分(2)求证:AD⊥PB.规范解答:(2)连接PG.
因为△PAD为正三角形,G为AD的中点,
所以PG⊥AD.…………………………………7分
由(1)知BG⊥AD,
而PG∩BG=G,
PG?平面PBG,
BG?平面PBG.
所以AD⊥平面PBG.…………………………10分
又因为PB?平面PBG,
所以AD⊥PB.……………………………………12分【2-2】 如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,点E为垂足.
(1)求证:PA⊥平面ABC;证明:(1)如图,在平面ABC内取一点D,作DF⊥AC于点F.
因为平面PAC⊥平面ABC,且交线为AC,
所以DF⊥平面PAC.
因为PA?平面PAC,所以DF⊥PA.
作DG⊥AB于点G,同理可证DG⊥PA.
因为DG,DF都在平面ABC内,
且DG∩DF=D,所以PA⊥平面ABC.(2)当点E为△PBC的垂心时,求证:△ABC是直角三角形.证明:(2)如图,连接BE并延长交PC于点H.
因为点E是△PBC的垂心,所以PC⊥BE.
又AE⊥平面PBC,PC?平面PBC,所以PC⊥AE.
因为AE∩BE=E,所以PC⊥平面ABE.
又AB?平面ABE,所以PC⊥AB.
由(1)知PA⊥平面ABC,
又AB?平面ABC,所以PA⊥AB.
因为PA∩PC=P,所以AB⊥平面PAC.
又AC?平面PAC,所以AB⊥AC,
即△ABC是直角三角形.方法技巧 利用面面垂直的性质定理,证明线面垂直的问题时,要注意以下三点:(1)两个平面垂直;(2)直线必须在其中一个平面内;(3)直线必须垂直于它们的交线.即时训练2-1:如图,平行四边形ABCD中,BD=2 ,AB=2,AD=4,将△BCD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.证明:因为AB=2,BD=2 ,AD=4,所以AB2+BD2=AD2,
所以AB⊥BD,
因为平面EBD⊥平面ABD,
平面EBD∩平面ABD=BD,
所以AB⊥平面EBD,
因为DE?平面EBD,
所以AB⊥DE.求证:AB⊥DE.2-2:如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.
(1)求证:BC⊥平面ACD;法二 取AC的中点O,连接OD,则OD⊥AC,
因为平面ADC⊥平面ABC,
平面ADC∩平面ABC=AC,DO?平面ACD,
所以DO⊥平面ABC,
所以OD⊥BC,又因为AC⊥BC,AC∩OD=O,
所以BC⊥平面BCD.(2)求几何体D-ABC的体积.题型三 线面、面面垂直的综合问题【例3】 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=
PC=4,AB=6,BC=3.
(1)证明:BC∥平面PDA;(1)证明:因为长方形ABCD中,BC∥AD,
又BC?平面PDA,AD?平面PDA,
所以BC∥平面PDA.(2)证明:BC⊥PD;(2)证明:取CD的中点H,连接PH,
因为PD=PC,所以PH⊥CD.
又因为平面PDC⊥平面ABCD,
平面PDC∩平面ABCD=CD,
所以PH⊥平面ABCD.
又因为BC?平面ABCD,所以PH⊥BC.
又因为长方形ABCD中,BC⊥CD,PH∩CD=H,
所以BC⊥平面PDC.
又因为PD?平面PDC,所以BC⊥PD.(3)求点C到平面PDA的距离.方法技巧 直线、平面之间的平行、垂直关系是重点考查的位置关系,当已知线面、面面垂直或平行时考虑用性质定理转化,要证线面、面面垂直或平行时要用判定定理进行论证.即时训练3-1:如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,
EP⊥平面ABCD.证明:(1)在矩形ABCD中,
因为AP=PB,DQ=QC,
所以AP CQ.
所以AQCP为平行四边形.
所以CP∥AQ.
因为CP?平面CEP,AQ?平面CEP,
所以AQ∥平面CEP.(1)求证:AQ∥平面CEP;(2)求证:平面AEQ⊥平面DEP.证明:(2)因为EP⊥平面ABCD,AQ?平面ABCD,
所以AQ⊥EP.
因为AB=2BC,P为AB的中点,所以AP=AD.连接PQ,则四边形ADQP为正方形.
所以AQ⊥DP.又EP∩DP=P,所以AQ⊥平面DEP.
因为AQ?平面AEQ,
所以平面AEQ⊥平面DEP.3-2:如图,在矩形ABCD中,AB=2AD,E为AB的中点,N为BC的中点,沿DE将△ADE折起.
(1)若平面ADE⊥平面BCDE,求证:AB=AC;证明:(1)取DE的中点M,连接AM,
因为在翻折前,四边形ABCD为矩形,AB=2AD,E为AB的中点,
所以翻折后AD=AE,则AM⊥DE,
又平面ADE⊥平面BCDE,所以AM⊥平面BCDE,
所以AM⊥BC,又N为BC的中点,所以MN⊥BC,
因为AM∩MN=M,
所以BC⊥平面AMN,所以BC⊥AN,
又N为BC的中点,所以AB=AC.(2)若AB=AC,求证:平面ADE⊥平面BCDE.证明:(2)由(1)设M是DE中点,因为N为BC的中点,
所以MN∥DC,又BC⊥DC,所以MN⊥BC,
又AB=AC,所以BC⊥AN,又MN∩AN=N,
所以BC⊥平面AMN,
所以BC⊥AM,由(1)知AM⊥DE,又DE与BC不平行,
所以AM⊥平面BCDE,又AM?平面ADE,
所以平面ADE⊥平面BCDE.
2.3.4 平面与平面垂直的性质课标要求:理解直线与平面垂直、平面与平面垂直的性质,并能运用性质定理解决一些简单问题.自主学习知识探究1.直线与平面垂直的性质定理a∥b 探究1:(教师备用)(1)垂直于同一个平面的两条直线一定共面吗?
(2)三角形的两边可以垂直于同一个平面吗?
(3)过一点有几条直线与已知平面垂直?
答案:(1)共面.由线面垂直的性质定理可知这两条直线是平行的,故能确定一个平面.
(2)不可以.若三角形的两边垂直于同一个平面,则这两条边平行,不能构成三角形.
(3)有且仅有一条.假设过一点有两条直线与已知平面垂直,由直线与平面垂直的性质定理可得这两条直线平行,应无公共点,这与过同一点相矛盾,故只有一条直线.2.平面与平面垂直的性质定理垂直于交线 探究2:(教师备用)(1)如果α⊥β,则α内的直线必垂直于β内的无数条直线吗?
(2)如果α⊥β,过β内的任意一点作α与β交线的垂线,则这条直线必垂直于α吗?
答案:(1)正确.若设α∩β=l,a?α,b?β,b⊥l,则a⊥b,故β内与b平行的无数条直线均垂直于α内的任意直线.
(2)错误.垂直于交线的直线必须在平面β内才与平面α垂直,否则不垂直.3.空间位置关系的相互转化
垂直关系之间的相互转化自我检测(教师备用)1.如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,平面PAC⊥平面ABC,则下列结论中错误的是( )
(A)AP⊥AC
(B)AP⊥AB
(C)AP⊥平面ABC
(D)AP与BC所成的角为45°D2.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
(A)若α⊥β,m?α,n?β,则m⊥n
(B)若α∥β,m?α,n?β,则m∥n
(C)若m⊥n,m?α,n?β,则α⊥β
(D)若m⊥α,m∥n,n∥β,则α⊥βD 3.已知m,n是两条不同的直线,α,β是两个不同的平面,且m∥α,n?β,则下列叙述正确的是( )
(A)若α∥β,则m∥n (B)若m∥n,则α∥β
(C)若n⊥α,则m⊥β (D)若m⊥β,则α⊥βD 4.如图所示,在三棱柱ABC-A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在平面ABC上的射影H必在直线 上.?答案:AB5.设α,β是空间两个不同的平面,m,n是平面α及β外的两条不同直线.从“①m⊥n;②α⊥β;③n⊥β;④m⊥α”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题: (用序号表示).?答案:①③④?②(或②③④?①)题型一 直线与平面垂直的性质定理的应用【例1】 (1)已知两条直线m,n,两个平面α,β,给出下面四个命题:
①m∥n,m⊥α?n⊥α;②α∥β,m?α,n?β?m∥n;③m∥n,m∥α?
n∥α;④α∥β,m∥n,m⊥α?n⊥β.
其中正确命题的序号是( )
(A)①③ (B)②④ (C)①④ (D)②③课堂探究(1)解析:由线面垂直的性质定理可知①正确;对于②,当α∥β,m?α,
n?β时,m与n可能平行也可能异面,故②不正确;对于③,当m∥n,m∥α时,n∥α或n?α,故③不正确;对于④,由m∥n,m⊥α,得n⊥α,又α∥β,所以n⊥β,故④正确.故选C.(2)如图所示,在正方体ABCD-A1B1C1D1中,M是AB上的一点,N是A1C的中点,
MN⊥平面A1DC.
求证:①MN∥AD1;(2)证明:①因为ABCD-A1B1C1D1为正方体,
所以AD1⊥A1D.
又因为CD⊥平面ADD1A1,AD1?平面ADD1A1,
所以CD⊥AD1.因为A1D∩CD=D,
所以AD1⊥平面A1DC.
又因为MN⊥平面A1DC,
所以MN∥AD1.②M是AB的中点.方法技巧 证明两条直线平行的方法常见的有:(1)公理4:平行于同一条直线的两条直线平行;(2)线面平行的性质定理:如果一条直线与一个平面平行,那么经过这条直线的任一平面与此平面的交线与该直线平行;(3)面面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行;(4)线面垂直的性质定理:垂直于同一个平面的两条直线平行.即时训练1-1:如图所示,已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于点E,过点E作EF⊥SC交SC于点F.
(1)求证:AF⊥SC;证明:(1)因为SA⊥平面AC,BC?平面AC,所以SA⊥BC,
因为ABCD为矩形,所以AB⊥BC,
又SA∩AB=A,所以BC⊥平面SAB,所以BC⊥AE.
又SB⊥AE,BC∩SB=B,所以AE⊥平面SBC,所以AE⊥SC.
又EF⊥SC,AE∩EF=E,所以SC⊥平面AEF,所以AF⊥SC.(2)若平面AEF交SD于点G.求证:AG⊥SD.证明:(2)因为SA⊥平面AC,所以SA⊥DC,
又AD⊥DC,SA∩AD=A,
所以DC⊥平面SAD.
所以DC⊥AG.
又由(1)有SC⊥平面AEF,AG?平面AEF,
所以SC⊥AG,
又DC∩SC=C,
所以AG⊥平面SDC,所以AG⊥SD.1-2:下列命题:
①垂直于同一条直线的两个平面互相平行;
②垂直于同一个平面的两条直线互相平行;
③一条直线在平面内,另一条直线与这个平面垂直,则这两条直线互相垂直.
其中正确的个数是( )
(A)0 (B)1 (C)2 (D)3解析:①②③均正确.故选D.题型二 平面与平面垂直的性质定理的应用【例2-1】 (12分)如图,P是四边形ABCD所在平面外一点,四边形ABCD是∠DAB=60°,且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD边的中点,求证:BG⊥平面PAD;规范解答:(1)如图所示,连接BD.
因为四边形ABCD是菱形,
且∠DAB=60°,所以△ABD是正三角形,…………………2分
因为G是AD的中点,所以BG⊥AD.…………………………3分
又因为平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD.所以BG⊥平面PAD.……………6分(2)求证:AD⊥PB.规范解答:(2)连接PG.
因为△PAD为正三角形,G为AD的中点,
所以PG⊥AD.…………………………………7分
由(1)知BG⊥AD,
而PG∩BG=G,
PG?平面PBG,
BG?平面PBG.
所以AD⊥平面PBG.…………………………10分
又因为PB?平面PBG,
所以AD⊥PB.……………………………………12分【2-2】 如图,平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,点E为垂足.
(1)求证:PA⊥平面ABC;证明:(1)如图,在平面ABC内取一点D,作DF⊥AC于点F.
因为平面PAC⊥平面ABC,且交线为AC,
所以DF⊥平面PAC.
因为PA?平面PAC,所以DF⊥PA.
作DG⊥AB于点G,同理可证DG⊥PA.
因为DG,DF都在平面ABC内,
且DG∩DF=D,所以PA⊥平面ABC.(2)当点E为△PBC的垂心时,求证:△ABC是直角三角形.证明:(2)如图,连接BE并延长交PC于点H.
因为点E是△PBC的垂心,所以PC⊥BE.
又AE⊥平面PBC,PC?平面PBC,所以PC⊥AE.
因为AE∩BE=E,所以PC⊥平面ABE.
又AB?平面ABE,所以PC⊥AB.
由(1)知PA⊥平面ABC,
又AB?平面ABC,所以PA⊥AB.
因为PA∩PC=P,所以AB⊥平面PAC.
又AC?平面PAC,所以AB⊥AC,
即△ABC是直角三角形.方法技巧 利用面面垂直的性质定理,证明线面垂直的问题时,要注意以下三点:(1)两个平面垂直;(2)直线必须在其中一个平面内;(3)直线必须垂直于它们的交线.即时训练2-1:如图,平行四边形ABCD中,BD=2 ,AB=2,AD=4,将△BCD沿BD折起到△EBD的位置,使平面EBD⊥平面ABD.证明:因为AB=2,BD=2 ,AD=4,所以AB2+BD2=AD2,
所以AB⊥BD,
因为平面EBD⊥平面ABD,
平面EBD∩平面ABD=BD,
所以AB⊥平面EBD,
因为DE?平面EBD,
所以AB⊥DE.求证:AB⊥DE.2-2:如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.
(1)求证:BC⊥平面ACD;法二 取AC的中点O,连接OD,则OD⊥AC,
因为平面ADC⊥平面ABC,
平面ADC∩平面ABC=AC,DO?平面ACD,
所以DO⊥平面ABC,
所以OD⊥BC,又因为AC⊥BC,AC∩OD=O,
所以BC⊥平面BCD.(2)求几何体D-ABC的体积.题型三 线面、面面垂直的综合问题【例3】 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,PD=
PC=4,AB=6,BC=3.
(1)证明:BC∥平面PDA;(1)证明:因为长方形ABCD中,BC∥AD,
又BC?平面PDA,AD?平面PDA,
所以BC∥平面PDA.(2)证明:BC⊥PD;(2)证明:取CD的中点H,连接PH,
因为PD=PC,所以PH⊥CD.
又因为平面PDC⊥平面ABCD,
平面PDC∩平面ABCD=CD,
所以PH⊥平面ABCD.
又因为BC?平面ABCD,所以PH⊥BC.
又因为长方形ABCD中,BC⊥CD,PH∩CD=H,
所以BC⊥平面PDC.
又因为PD?平面PDC,所以BC⊥PD.(3)求点C到平面PDA的距离.方法技巧 直线、平面之间的平行、垂直关系是重点考查的位置关系,当已知线面、面面垂直或平行时考虑用性质定理转化,要证线面、面面垂直或平行时要用判定定理进行论证.即时训练3-1:如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,
EP⊥平面ABCD.证明:(1)在矩形ABCD中,
因为AP=PB,DQ=QC,
所以AP CQ.
所以AQCP为平行四边形.
所以CP∥AQ.
因为CP?平面CEP,AQ?平面CEP,
所以AQ∥平面CEP.(1)求证:AQ∥平面CEP;(2)求证:平面AEQ⊥平面DEP.证明:(2)因为EP⊥平面ABCD,AQ?平面ABCD,
所以AQ⊥EP.
因为AB=2BC,P为AB的中点,所以AP=AD.连接PQ,则四边形ADQP为正方形.
所以AQ⊥DP.又EP∩DP=P,所以AQ⊥平面DEP.
因为AQ?平面AEQ,
所以平面AEQ⊥平面DEP.3-2:如图,在矩形ABCD中,AB=2AD,E为AB的中点,N为BC的中点,沿DE将△ADE折起.
(1)若平面ADE⊥平面BCDE,求证:AB=AC;证明:(1)取DE的中点M,连接AM,
因为在翻折前,四边形ABCD为矩形,AB=2AD,E为AB的中点,
所以翻折后AD=AE,则AM⊥DE,
又平面ADE⊥平面BCDE,所以AM⊥平面BCDE,
所以AM⊥BC,又N为BC的中点,所以MN⊥BC,
因为AM∩MN=M,
所以BC⊥平面AMN,所以BC⊥AN,
又N为BC的中点,所以AB=AC.(2)若AB=AC,求证:平面ADE⊥平面BCDE.证明:(2)由(1)设M是DE中点,因为N为BC的中点,
所以MN∥DC,又BC⊥DC,所以MN⊥BC,
又AB=AC,所以BC⊥AN,又MN∩AN=N,
所以BC⊥平面AMN,
所以BC⊥AM,由(1)知AM⊥DE,又DE与BC不平行,
所以AM⊥平面BCDE,又AM?平面ADE,
所以平面ADE⊥平面BCDE.
