高中数学新人教A版必修2课件:第三章直线与方程(37张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第三章直线与方程(37张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 16:50:14 | ||
图片预览











文档简介
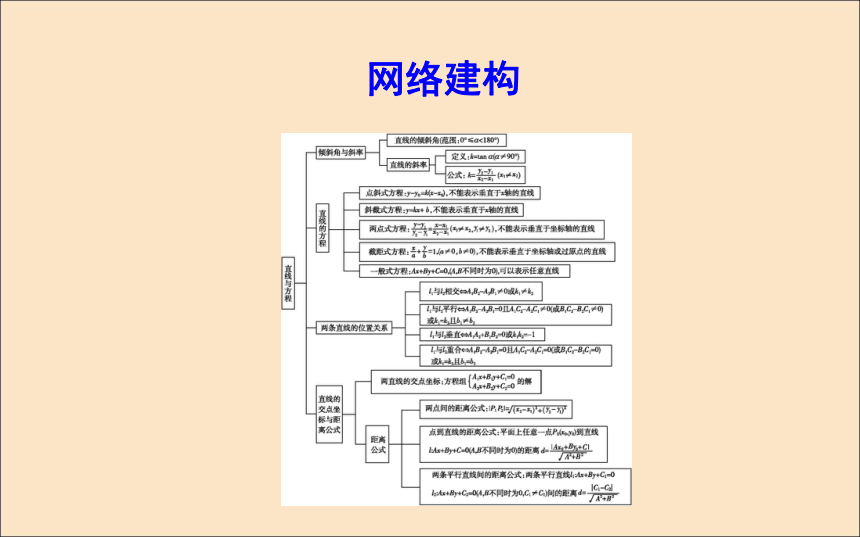
课件37张PPT。章末总结网络建构一、直线的斜率与倾斜角
【典例1】 (1)求经过下列两点的直线的倾斜角和斜率.
①A(-2,0),B(-5,3);②A(3,2),B(5,2);③A(3,-1),B(3,3);主题串讲③因为A(3,-1),B(3,3);
所以直线l的倾斜角为90°.(2)已知直线l过点A(2,1),B(m,3),求直线l的倾斜角的范围.规律方法 直线倾斜角和斜率及其关系
(1)倾斜角α的范围是0°≤α<180°.
(2)倾斜角α与斜率k的对应关系
①α≠90°时,k=tan α;
②α=90°时,k不存在.
(3)倾斜角与斜率的单调性问题
当直线l的倾斜角为α∈[0°,90°)时,直线l的斜率将随着角度的增大而增大;
当直线l的倾斜角α∈(90°,180°)时,直线l的斜率将随着角度的增大而减小.二、直线的方程
【典例2】 根据所给条件求直线的方程:
(1)直线过点(-4,0),倾斜角的正弦值为 ;(2)直线过点(5,10),到原点的距离为5;(3)过点A(-5,-4)作直线l,使它与两坐标轴相交且与两轴所围成的三角形面积为5,求直线l的方程.规律方法 在求直线方程时,应先选择适当的直线方程的形式,并注意各种形式的适用条件.用斜截式及点斜式时,直线的斜率必须存在,而两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直或经过原点的直线.故在解题时,若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况.三、两条直线的位置关系
【典例3】 已知两条直线l1:mx+8y+n=0和l2:2x+my-1=0,试确定m,n的值,使:
(1)l1与l2相交于点(m,-1); (2)l1∥l2;解:(1)因为l1与l2相交于点(m,-1),所以点(m,-1)在l1,l2上,将(m,-1)代入l2的方程,得2m-m-1=0,解得m=1.
所以直线l1的方程为x+8y+n=0,所以n=7.(3)l1⊥l2,且l1在y轴上的截距为-1.规律方法 两直线平行与垂直的判定
(1)两条直线l1:y=k1x+b1,l2:y=k2x+b2斜率都存在,l1∥l2?k1=k2且b1≠b2;l1⊥l2?k1·k2=-1,斜率不存在时单独考虑,即k1,k2中有一个为零,另一个不存在,则两条直线垂直,若k1,k2均不存在,则两直线平行.
(2)当两条直线给出一般式时,平行与垂直关系利用系数关系解决.即l1:A1x+B1y+C1=0;l2:A2x+B2y+C2=0.l1∥l2?A1B2-A2B1=0,且B1C2-B2C1≠0;l1⊥l2?A1A2+B1B2=0.即时训练3-1:已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0.
(1)试判断l1与l2是否平行;(2)当l1⊥l2时,求a的值.四、距离问题
【典例4】 已知正方形的中心为(0,-1),其中一条边所在直线的方程为3x+y-2=0.求其他三条边所在直线的方程.即时训练4-1:若倾斜角为45°的直线m被平行线l1:x+y-1=0与l2:x+y-3=0所截得的线段为AB,则AB的长为 .?五、对称问题
【典例5】 已知直线l:2x-3y+1=0,点A(-1,-2),求:
(1)点A关于直线l的对称点A'的坐标;(2)直线m:3x-2y-6=0关于直线l的对称直线m'的方程;(3)直线l关于点A(-1,-2)对称的直线l'的方程.规律方法 求对称直线的方程,可以转化为点对称问题解决或者用相关点转移法解决.即时训练5-1:(2016·浙江杭州高一检测)已知直线y=2x是△ABC中∠C的平分线所在的直线,若点A,B的坐标分别是(-4,2),(3,1),则点C的坐标为( )
(A)(-2,4) (B)(-2,-4)
(C)(2,4) (D)(2,-4)六、最值问题
【典例6】 已知A(4,1),B(0,4)两点,在直线l:3x-y-1=0上找一点M,使得||MA|-|MB||的值最大,并求此时点M的坐标及最大值.规律方法 本题是对称问题在求线段和、差的最值上的应用,利用对称问题可以解决类似的两类问题:一类是在定直线上找一点M,使点M到两定点A,B的距离之差||MA|-|MB||最大;一类是在定直线上找一点M,使点M到两定点A,B的距离之和||MA|+|MB||最小,这时还要考虑A,B两点在直线的同侧还是异侧.即时训练6-1:已知0【典例7】 已知直线l过点A(1,2),且原点到直线l的距离为1,求直线l的方程.即时训练7-1:设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求直线l的方程;
(2)若l在两坐标轴上的截距互为相反数,求a.真题体验1.(2014·四川卷,文9)设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),则|PA|+|PB|的取值范围是( )B2.(2013·辽宁卷,理9)已知点O(0,0),A(0,b),B(a,a3).若△OAB为直角三角形,则必有( )C3.(2013·湖南卷,理8)在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )D答案:85.(2016·上海卷,理3)已知平行直线l1:2x+y-1=0,l2:2x+y+1=0,则l1,l2的距离 .?6.(2013·四川卷,文15)在平面直角坐标系内,到点A(1,2),B(1,5),C(3,6),
D(7,-1)的距离之和最小的点的坐标是 .?答案:(2,4)
【典例1】 (1)求经过下列两点的直线的倾斜角和斜率.
①A(-2,0),B(-5,3);②A(3,2),B(5,2);③A(3,-1),B(3,3);主题串讲③因为A(3,-1),B(3,3);
所以直线l的倾斜角为90°.(2)已知直线l过点A(2,1),B(m,3),求直线l的倾斜角的范围.规律方法 直线倾斜角和斜率及其关系
(1)倾斜角α的范围是0°≤α<180°.
(2)倾斜角α与斜率k的对应关系
①α≠90°时,k=tan α;
②α=90°时,k不存在.
(3)倾斜角与斜率的单调性问题
当直线l的倾斜角为α∈[0°,90°)时,直线l的斜率将随着角度的增大而增大;
当直线l的倾斜角α∈(90°,180°)时,直线l的斜率将随着角度的增大而减小.二、直线的方程
【典例2】 根据所给条件求直线的方程:
(1)直线过点(-4,0),倾斜角的正弦值为 ;(2)直线过点(5,10),到原点的距离为5;(3)过点A(-5,-4)作直线l,使它与两坐标轴相交且与两轴所围成的三角形面积为5,求直线l的方程.规律方法 在求直线方程时,应先选择适当的直线方程的形式,并注意各种形式的适用条件.用斜截式及点斜式时,直线的斜率必须存在,而两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直或经过原点的直线.故在解题时,若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况.三、两条直线的位置关系
【典例3】 已知两条直线l1:mx+8y+n=0和l2:2x+my-1=0,试确定m,n的值,使:
(1)l1与l2相交于点(m,-1); (2)l1∥l2;解:(1)因为l1与l2相交于点(m,-1),所以点(m,-1)在l1,l2上,将(m,-1)代入l2的方程,得2m-m-1=0,解得m=1.
所以直线l1的方程为x+8y+n=0,所以n=7.(3)l1⊥l2,且l1在y轴上的截距为-1.规律方法 两直线平行与垂直的判定
(1)两条直线l1:y=k1x+b1,l2:y=k2x+b2斜率都存在,l1∥l2?k1=k2且b1≠b2;l1⊥l2?k1·k2=-1,斜率不存在时单独考虑,即k1,k2中有一个为零,另一个不存在,则两条直线垂直,若k1,k2均不存在,则两直线平行.
(2)当两条直线给出一般式时,平行与垂直关系利用系数关系解决.即l1:A1x+B1y+C1=0;l2:A2x+B2y+C2=0.l1∥l2?A1B2-A2B1=0,且B1C2-B2C1≠0;l1⊥l2?A1A2+B1B2=0.即时训练3-1:已知直线l1:ax+2y+6=0和直线l2:x+(a-1)y+a2-1=0.
(1)试判断l1与l2是否平行;(2)当l1⊥l2时,求a的值.四、距离问题
【典例4】 已知正方形的中心为(0,-1),其中一条边所在直线的方程为3x+y-2=0.求其他三条边所在直线的方程.即时训练4-1:若倾斜角为45°的直线m被平行线l1:x+y-1=0与l2:x+y-3=0所截得的线段为AB,则AB的长为 .?五、对称问题
【典例5】 已知直线l:2x-3y+1=0,点A(-1,-2),求:
(1)点A关于直线l的对称点A'的坐标;(2)直线m:3x-2y-6=0关于直线l的对称直线m'的方程;(3)直线l关于点A(-1,-2)对称的直线l'的方程.规律方法 求对称直线的方程,可以转化为点对称问题解决或者用相关点转移法解决.即时训练5-1:(2016·浙江杭州高一检测)已知直线y=2x是△ABC中∠C的平分线所在的直线,若点A,B的坐标分别是(-4,2),(3,1),则点C的坐标为( )
(A)(-2,4) (B)(-2,-4)
(C)(2,4) (D)(2,-4)六、最值问题
【典例6】 已知A(4,1),B(0,4)两点,在直线l:3x-y-1=0上找一点M,使得||MA|-|MB||的值最大,并求此时点M的坐标及最大值.规律方法 本题是对称问题在求线段和、差的最值上的应用,利用对称问题可以解决类似的两类问题:一类是在定直线上找一点M,使点M到两定点A,B的距离之差||MA|-|MB||最大;一类是在定直线上找一点M,使点M到两定点A,B的距离之和||MA|+|MB||最小,这时还要考虑A,B两点在直线的同侧还是异侧.即时训练6-1:已知0
(1)若l在两坐标轴上的截距相等,求直线l的方程;
(2)若l在两坐标轴上的截距互为相反数,求a.真题体验1.(2014·四川卷,文9)设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),则|PA|+|PB|的取值范围是( )B2.(2013·辽宁卷,理9)已知点O(0,0),A(0,b),B(a,a3).若△OAB为直角三角形,则必有( )C3.(2013·湖南卷,理8)在等腰直角三角形ABC中,AB=AC=4,点P是边AB上异于A,B的一点.光线从点P出发,经BC,CA反射后又回到点P(如图).若光线QR经过△ABC的重心,则AP等于( )D答案:85.(2016·上海卷,理3)已知平行直线l1:2x+y-1=0,l2:2x+y+1=0,则l1,l2的距离 .?6.(2013·四川卷,文15)在平面直角坐标系内,到点A(1,2),B(1,5),C(3,6),
D(7,-1)的距离之和最小的点的坐标是 .?答案:(2,4)
