高中数学新人教A版必修2课件:第三章直线与方程3.2.1直线的点斜式方程(28张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第三章直线与方程3.2.1直线的点斜式方程(28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 16:51:17 | ||
图片预览







文档简介
课件28张PPT。3.2 直线的方程
3.2.1 直线的点斜式方程课标要求:1.了解直线的点斜式方程的推导过程.2.掌握直线的点斜式方程并会应用.3.掌握直线的斜截式方程,了解截距的概念.自主学习知识探究1.直线的点斜式方程的定义
已知直线l经过点P0(x0,y0),且斜率为k,则直线l的方程为 .
这个方程是由直线上一定点及其斜率确定的,因此称为直线的点斜式方程,简称点斜式.
注意:点斜式方程的应用前提是直线的斜率存在,若斜率不存在,则直线的方程不能用点斜式表示.y-y0=k(x-x0)2.点斜式方程的特殊情形
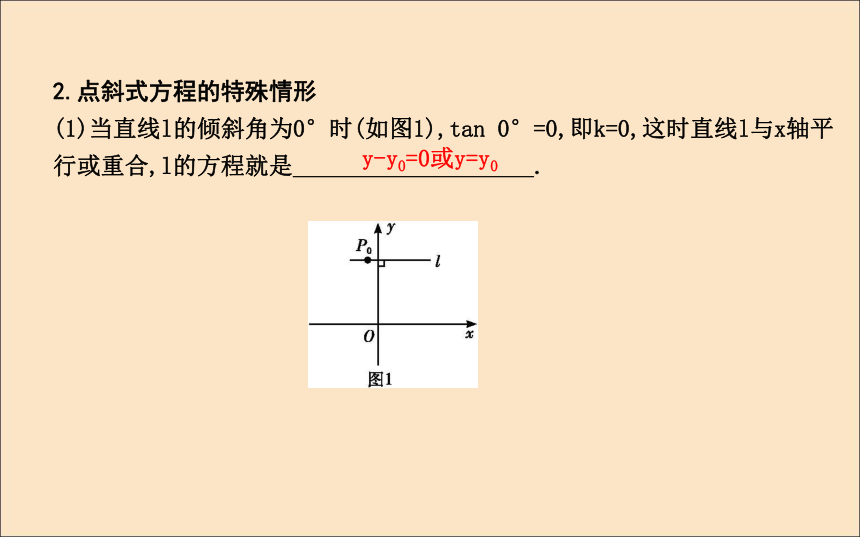
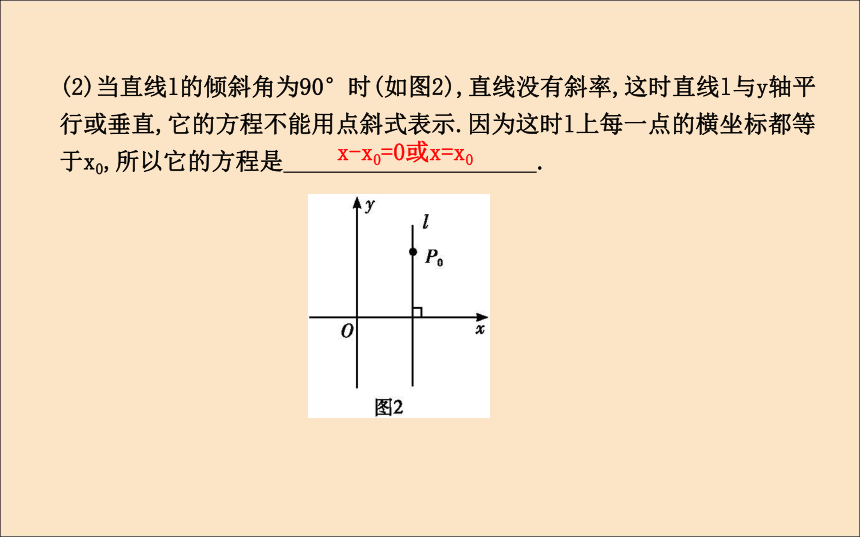
(1)当直线l的倾斜角为0°时(如图1),tan 0°=0,即k=0,这时直线l与x轴平行或重合,l的方程就是 .y-y0=0或y=y0(2)当直线l的倾斜角为90°时(如图2),直线没有斜率,这时直线l与y轴平行或垂直,它的方程不能用点斜式表示.因为这时l上每一点的横坐标都等于x0,所以它的方程是 .x-x0=0或x=x0注意:(1) =k与y-y0=k(x-x0)是不同的,前者表示的直线上缺少一个点P0(x0,y0),后者才表示整条直线.
(2)经过点P0(x0,y0)的直线有无数条,可分为两类:①斜率存在的直线,方程为y-y0=k(x-x0);②斜率不存在的直线,方程为x=x0.
3.直线的斜截式方程
我们把直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距.
如果直线l的斜率为k, 且在y轴上的截距为b, 则方程为y-b=k(x-0),即
,叫做直线的斜截式方程,简称斜截式.
当b=0时,y=kx表示过原点的直线;当k=0且b≠0时,y=b表示与x轴平行的直线;当k=0且b=0时,y=0表示与x轴重合的直线.y=kx+b注意:(1)直线的斜截式方程其实是点斜式方程在x0=0时的特殊情况,斜截式方程应用的前提是直线的斜率存在.
(2)斜截式方程与一次函数的解析式相同,都是y=kx+b的形式,但有区别:当k≠0时,y=kx+b为一次函数;当k=0时,y=b,不是一次函数,故一次函数y=kx+b(k≠0)一定可看成一条直线的斜截式方程.
(3)纵截距不是距离,它是直线与y轴交点的纵坐标,所以可取一切实数,即可为正数、零或负数.当直线l与y轴正半轴相交时,截距b>0,但并非所有的直线都与y轴有交点,当直线l与y轴平行时,l在y轴上没有截距.(4)由于有些直线没有斜率,即有些直线在y轴上没有截距,所以并非所有直线都可以用斜截式表示.当直线与x轴垂直时,直线不能用斜截式表示,这时其方程可以表示为x=x1(x1为直线与x轴交点的横坐标).
(5)方程y=kx+b中,y的系数是1,x的系数是k,常数项是b.k,b有明显的几何意义,其中k是直线的斜率,b是直线与y轴交点的纵坐标,即在y轴上的截距.自我检测(教师备用)1.过点P(2,-1),斜率为 的直线的点斜式方程为( )CC3.已知直线的方程是y+2=-x-1,则( )
(A)直线经过点(-1,2),斜率为-1
(B)直线经过点(2,-1),斜率为-1
(C)直线经过点(-1,-2),斜率为-1
(D)直线经过点(-2,-1),斜率为1C解析:直线方程可化为y-(-2)=-[x-(-1)],故直线经过点(-1,-2),斜率为-1.故选C.4.在y轴上的截距为2,且与直线y=-3x-4平行的直线的斜截式方程为 .?答案:y=-3x+25.若直线l过点(0,7),且与直线y=-4x+2垂直,则直线l的方程为 .?题型一 直线的点斜式方程课堂探究【1-2】 已知在第一象限的△ABC中,A(1,1),B(5,1),∠A=60°,∠B=45°,求:
(1)AB所在直线的方程;解析:(1)如图所示,直线AB过点(1,1)且与x轴平行,故AB所在直线方程是y=1.(2)AC边与BC边所在直线的方程.误区警示 已知直线上一点的坐标以及直线斜率或已知直线上两点的坐标,均可用直线方程的点斜式表示,直线方程的点斜式,应在直线斜率存在的条件下使用.当直线的斜率不存在时,直线方程为x=x0.即时训练1-1:已知三角形的顶点坐标是A(-5,0),B(3,-3),C(0,2),试求这个三角形的三条边所在直线的方程.题型二 直线的斜截式方程【例2】写出下列直线的斜截式方程:
①直线的倾斜角是60°,在y轴上的截距是5;
②直线在x轴上的截距为4,在y轴上的截距为-2.【2-2】 已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相同,求直线l的方程.解:由题知,直线l与l1平行,所以直线l的斜率为-2,直线l与l2在y轴上的截距相同,故在y轴上的截距是-2,由斜截式方程知l的方程为y=-2x-2.变式探究:若将本例中“直线l与l1平行”改为“直线l与l1垂直”,其他条件不变,又如何求解?方法技巧 直线的斜截式方程的求解策略
(1)求直线的斜截式方程只要分别求出直线的斜率和在y轴上的截距,代入方程即可.(2)当斜率和截距未知时,可结合已知条件,先求出斜率和截距,再写出直线的斜截式方程.即时训练2-1:根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
(2)倾斜角为30°,在y轴上的截距是-2;解:(1)由直线方程的斜截式可知,所求直线方程为y=2x+5.(3)倾斜角为60°,与y轴的交点到坐标原点的距离为3.题型三平行与垂直的应用【例3】 (1)当a为何值时,直线l1:y=-2x+2a与直线l2:y=(a2-3a)x+2平行,垂直;(2)若点A(1,2)在直线l上的射影为B(-1,4),求直线l的方程.方法技巧 设直线l1和l2的斜率k1,k2都存在,其方程分别为l1:y=k1x+b1,
l2:y=k2x+b2,那么①l1∥l2?k1=k2且b1≠b2;②k1=k2且b1=b2?两条直线重合;③l1⊥l2?k1·k2=-1.即时训练3-1:△ABC中,A(1,-1),B(4,a),C(3,3).若△ABC是以B为直角的直角三角形.
(1)求a;(2)求直线AB的方程.
3.2.1 直线的点斜式方程课标要求:1.了解直线的点斜式方程的推导过程.2.掌握直线的点斜式方程并会应用.3.掌握直线的斜截式方程,了解截距的概念.自主学习知识探究1.直线的点斜式方程的定义
已知直线l经过点P0(x0,y0),且斜率为k,则直线l的方程为 .
这个方程是由直线上一定点及其斜率确定的,因此称为直线的点斜式方程,简称点斜式.
注意:点斜式方程的应用前提是直线的斜率存在,若斜率不存在,则直线的方程不能用点斜式表示.y-y0=k(x-x0)2.点斜式方程的特殊情形
(1)当直线l的倾斜角为0°时(如图1),tan 0°=0,即k=0,这时直线l与x轴平行或重合,l的方程就是 .y-y0=0或y=y0(2)当直线l的倾斜角为90°时(如图2),直线没有斜率,这时直线l与y轴平行或垂直,它的方程不能用点斜式表示.因为这时l上每一点的横坐标都等于x0,所以它的方程是 .x-x0=0或x=x0注意:(1) =k与y-y0=k(x-x0)是不同的,前者表示的直线上缺少一个点P0(x0,y0),后者才表示整条直线.
(2)经过点P0(x0,y0)的直线有无数条,可分为两类:①斜率存在的直线,方程为y-y0=k(x-x0);②斜率不存在的直线,方程为x=x0.
3.直线的斜截式方程
我们把直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距.
如果直线l的斜率为k, 且在y轴上的截距为b, 则方程为y-b=k(x-0),即
,叫做直线的斜截式方程,简称斜截式.
当b=0时,y=kx表示过原点的直线;当k=0且b≠0时,y=b表示与x轴平行的直线;当k=0且b=0时,y=0表示与x轴重合的直线.y=kx+b注意:(1)直线的斜截式方程其实是点斜式方程在x0=0时的特殊情况,斜截式方程应用的前提是直线的斜率存在.
(2)斜截式方程与一次函数的解析式相同,都是y=kx+b的形式,但有区别:当k≠0时,y=kx+b为一次函数;当k=0时,y=b,不是一次函数,故一次函数y=kx+b(k≠0)一定可看成一条直线的斜截式方程.
(3)纵截距不是距离,它是直线与y轴交点的纵坐标,所以可取一切实数,即可为正数、零或负数.当直线l与y轴正半轴相交时,截距b>0,但并非所有的直线都与y轴有交点,当直线l与y轴平行时,l在y轴上没有截距.(4)由于有些直线没有斜率,即有些直线在y轴上没有截距,所以并非所有直线都可以用斜截式表示.当直线与x轴垂直时,直线不能用斜截式表示,这时其方程可以表示为x=x1(x1为直线与x轴交点的横坐标).
(5)方程y=kx+b中,y的系数是1,x的系数是k,常数项是b.k,b有明显的几何意义,其中k是直线的斜率,b是直线与y轴交点的纵坐标,即在y轴上的截距.自我检测(教师备用)1.过点P(2,-1),斜率为 的直线的点斜式方程为( )CC3.已知直线的方程是y+2=-x-1,则( )
(A)直线经过点(-1,2),斜率为-1
(B)直线经过点(2,-1),斜率为-1
(C)直线经过点(-1,-2),斜率为-1
(D)直线经过点(-2,-1),斜率为1C解析:直线方程可化为y-(-2)=-[x-(-1)],故直线经过点(-1,-2),斜率为-1.故选C.4.在y轴上的截距为2,且与直线y=-3x-4平行的直线的斜截式方程为 .?答案:y=-3x+25.若直线l过点(0,7),且与直线y=-4x+2垂直,则直线l的方程为 .?题型一 直线的点斜式方程课堂探究【1-2】 已知在第一象限的△ABC中,A(1,1),B(5,1),∠A=60°,∠B=45°,求:
(1)AB所在直线的方程;解析:(1)如图所示,直线AB过点(1,1)且与x轴平行,故AB所在直线方程是y=1.(2)AC边与BC边所在直线的方程.误区警示 已知直线上一点的坐标以及直线斜率或已知直线上两点的坐标,均可用直线方程的点斜式表示,直线方程的点斜式,应在直线斜率存在的条件下使用.当直线的斜率不存在时,直线方程为x=x0.即时训练1-1:已知三角形的顶点坐标是A(-5,0),B(3,-3),C(0,2),试求这个三角形的三条边所在直线的方程.题型二 直线的斜截式方程【例2】写出下列直线的斜截式方程:
①直线的倾斜角是60°,在y轴上的截距是5;
②直线在x轴上的截距为4,在y轴上的截距为-2.【2-2】 已知直线l1的方程为y=-2x+3,l2的方程为y=4x-2,直线l与l1平行且与l2在y轴上的截距相同,求直线l的方程.解:由题知,直线l与l1平行,所以直线l的斜率为-2,直线l与l2在y轴上的截距相同,故在y轴上的截距是-2,由斜截式方程知l的方程为y=-2x-2.变式探究:若将本例中“直线l与l1平行”改为“直线l与l1垂直”,其他条件不变,又如何求解?方法技巧 直线的斜截式方程的求解策略
(1)求直线的斜截式方程只要分别求出直线的斜率和在y轴上的截距,代入方程即可.(2)当斜率和截距未知时,可结合已知条件,先求出斜率和截距,再写出直线的斜截式方程.即时训练2-1:根据条件写出下列直线的斜截式方程:
(1)斜率为2,在y轴上的截距是5;
(2)倾斜角为30°,在y轴上的截距是-2;解:(1)由直线方程的斜截式可知,所求直线方程为y=2x+5.(3)倾斜角为60°,与y轴的交点到坐标原点的距离为3.题型三平行与垂直的应用【例3】 (1)当a为何值时,直线l1:y=-2x+2a与直线l2:y=(a2-3a)x+2平行,垂直;(2)若点A(1,2)在直线l上的射影为B(-1,4),求直线l的方程.方法技巧 设直线l1和l2的斜率k1,k2都存在,其方程分别为l1:y=k1x+b1,
l2:y=k2x+b2,那么①l1∥l2?k1=k2且b1≠b2;②k1=k2且b1=b2?两条直线重合;③l1⊥l2?k1·k2=-1.即时训练3-1:△ABC中,A(1,-1),B(4,a),C(3,3).若△ABC是以B为直角的直角三角形.
(1)求a;(2)求直线AB的方程.
