高中数学新人教A版必修2课件:第四章圆与方程4.3.1空间直角坐标系4.3.2空间两点间的距离公式(31张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第四章圆与方程4.3.1空间直角坐标系4.3.2空间两点间的距离公式(31张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 17:00:49 | ||
图片预览










文档简介
课件31张PPT。4.3 空间直角坐标系
4.3.1 空间直角坐标系
4.3.2 空间两点间的距离公式课标要求:1.理解空间直角坐标系的有关概念,会根据坐标描出点的位置、由点的位置写出点的坐标.2.掌握空间两点间的距离公式,理解公式使用的条件,会用公式计算或证明.自主学习知识探究1.空间直角坐标系的有关概念
如图,为了确定空间点的位置,我们建立空间直角坐标系.以单位正方体为截体.以O为原点,分别以射线OA,OC,OD′的方向为正方向,以线段OA,OC,OD′的长为单位长,建立三条数轴:x轴、y轴、z轴.这时,我们说建立了一个空间直角坐标系O-xyz,其中点O叫坐标原点,x轴、y轴、z轴叫坐标轴,通过每两个坐标轴的平面叫坐标平面,分别称为xOy平面、yOz平面、zOx平面,通常建立的坐标系为右手直角坐标系,即右手拇指指向x轴的正方向,食指指向y轴的正方向,中指指向z轴的正方向.2.空间任意点与有序数组(x,y,z)之间的对应法则
(1)过点P作一个平面平行于平面yOz(这样构造的平面同样垂直于x轴),这个平面与x轴的交点记为Px,它在x轴上的坐标为x,这个数x就叫做点P的x坐标或横坐标.
(2)过点P作一个平面平行于平面xOz(垂直于y轴),这个平面与y轴的交点记作Py,它在y轴上的坐标为y,这个数y叫做点P的y坐标或纵坐标.
(3)过点P作一个平面平行于平面xOy(垂直于z轴),这个平面与z轴的交点记作Pz,它在z轴上的坐标为z,这个数z叫做点P的z坐标或竖坐标.(3)关于点对称
点A关于点P的对称点为B?AB的中点为P,所以欲求点A关于点P的对称点,只需利用空间两点的中点坐标公式列方程求解即可.特别地,点A(x,y,z)关于原点的对称点为B(-x,-y,-z).自我检测(教师备用)1.点(0,2,1)位于( )
(A)y轴上 (B)z轴上
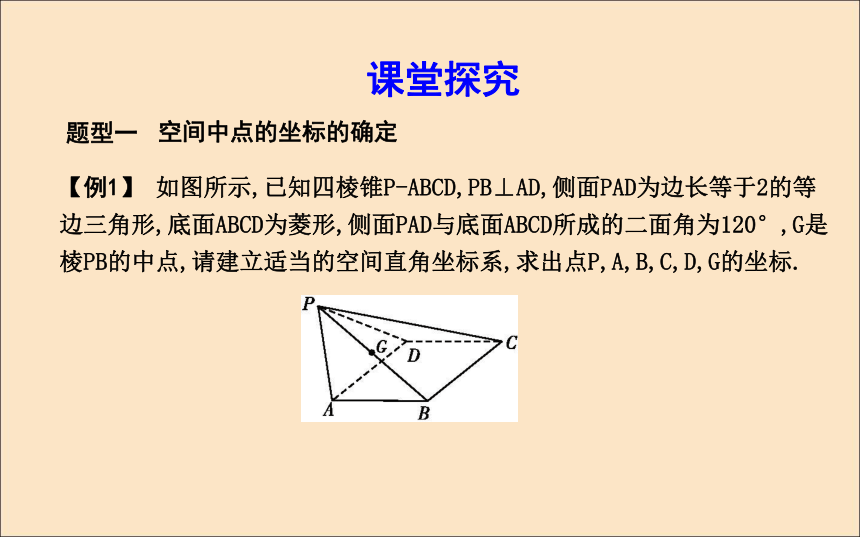
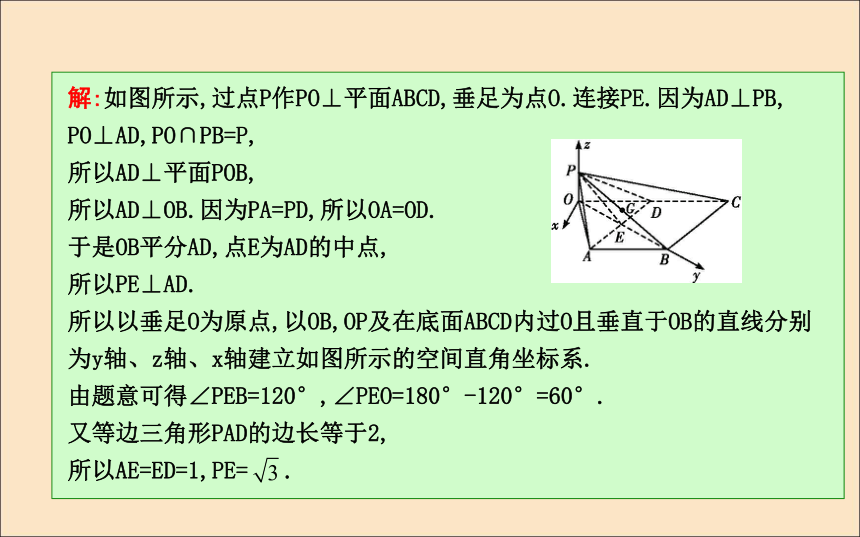
(C)xOy面上 (D)yOz面上DDA4.点P(-3,2,-1)关于平面xOy的对称点是 .?答案:(-3,2,1)5.设A(3,3,1),B(1,0,5),C(0,1,0),则AB的中点M到点C的距离|CM|= .?答案:题型一 空间中点的坐标的确定【例1】 如图所示,已知四棱锥P-ABCD,PB⊥AD,侧面PAD为边长等于2的等边三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°,G是棱PB的中点,请建立适当的空间直角坐标系,求出点P,A,B,C,D,G的坐标.课堂探究解:如图所示,过点P作PO⊥平面ABCD,垂足为点O.连接PE.因为AD⊥PB,
PO⊥AD,PO∩PB=P,
所以AD⊥平面POB,
所以AD⊥OB.因为PA=PD,所以OA=OD.
于是OB平分AD,点E为AD的中点,
所以PE⊥AD.
所以以垂足O为原点,以OB,OP及在底面ABCD内过O且垂直于OB的直线分别为y轴、z轴、x轴建立如图所示的空间直角坐标系.
由题意可得∠PEB=120°,∠PEO=180°-120°=60°.
又等边三角形PAD的边长等于2,
所以AE=ED=1,PE= .方法技巧 (1)建立空间直角坐标系时,要考虑如何建系才能使点的坐标简单、便于计算,一般是要使尽量多的点落在坐标轴上.
(2)对于长方体或正方体,一般取相邻的三条棱为x,y,z轴建立空间直角坐标系;确定点的坐标时,最常用的方法就是求某些与轴平行的线段的长度,即将坐标转化为与轴平行的线段长度,同时要注意坐标的符号,这也是求空间点的坐标的关键.即时训练1-1:如图,在长方体ABCD-A1B1C1D1中,E,F分别是棱BC,CC1上的点,
|CF|=|AB|=2|CE|,|AB|∶|AD|∶|AA1|=1∶2∶4.试建立适当的坐标系,写出E,F点的坐标.1-2:如图,长方体ABCD-A1B1C1D1中,|AB|=4,|AD|=3,|AA1|=5,N为棱CC1的中点,分别以AB,AD,AA1所在的直线为x,y,z轴,建立空间直角坐标系.
(1)求点A,B,C,D,A1,B1,C1,D1的坐标;解:(1)很明显A(0,0,0),
由于点B在x轴的正半轴上,且|OB|=4,所以B(4,0,0).同理,可得D(0,3,0),
A1(0,0,5).由于点C在坐标平面xOy内,BC⊥AB,CD⊥AD,则点C(4,3,0).
同理,可得B1(4,0,5),D1(0,3,5),与C的坐标相比,点C1的坐标中只有竖坐标不同,CC1=AA1=5,则点C1(4,3,5).(2)求点N的坐标.1-3:已知如图所示,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,且|PA|=|AB|=2,E为PD的中点.建立适当的坐标系,求A,B,C,D,P,E的坐标.解:如图所示,以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
由|PA|=|AB|=2,四边形ABCD为正方形,可知A,B,C,D,P,E的坐标分别为A(0,0,0,),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(0,1,1).题型二 空间直角坐标系中点的对称问题【例2】 已知点P(2,3,-1),求:
(1)点P关于各坐标平面对称的点的坐标;规范解答:(1)设点P关于xOy坐标平面的对称点为P′,则点P′在x轴上的坐标及在y轴上的坐标与点P在x轴上的坐标及在y轴上的坐标相同,而点P′在z轴上的坐标与点P在z轴上的坐标互为相反数.
所以,点P关于xOy坐标平面的对称点P′的坐标为(2,3,1).
同理,点P关于yOz,zOx坐标平面的对称点的坐标分别为(-2,3,-1),(2,
-3,-1).(2)点P关于各坐标轴对称的点的坐标;
(3)点P关于坐标原点对称的点的坐标.规范解答:(2)设点P关于x轴的对称点为Q,则点Q在x轴上的坐标与点P在x轴上的坐标相同,而点Q在y轴上的坐标及在z轴上的坐标与点P在y轴上的坐标及在z轴上的坐标互为相反数.
所以,点P关于x轴的对称点Q的坐标为(2,-3,1).
同理,点P关于y轴、z轴的对称点的坐标分别为(-2,3,1),(-2,-3,-1).
(3)点P(2,3,-1)关于坐标原点对称的点的坐标为(-2,-3,1).(4)点P关于点(1,2,-6)对称的点的坐标.即时训练2-1:(1)在空间直角坐标系中,点P(3,4,5)与点Q(3,-4,-5)两点的位置关系是( )
(A)关于x轴对称 (B)关于xOy平面对称
(C)关于坐标原点对称 (D)以上都不对
(2)在空间直角坐标系中,点P(-2,1,4)关于xOy平面对称的点的坐标是( )
(A)(-2,1,-4) (B)(-2,-1,-4)
(C)(2,-1,4) (D)(2,1,-4)解析:(1)由于P,Q两点的横坐标相等,纵坐标与竖坐标分别互为相反数,故P,Q两点关于x轴对称.故选A.
(2)过点P向xOy平面作垂线,垂足为N,则N就是点P与它关于xOy平面的对称点的中点,因为N的坐标为(-2,1,0),所以对称点的坐标为(-2,1,-4),故选A.2-2:在空间直角坐标系中有一个点P(1,3,-2),求:
(1)点P关于坐标原点O的对称点P1的坐标;解:(1)设点P1的坐标为(x1,y1,z1),因为点P和P1关于坐标原点O对称,所
以点O为线段PP1的中点,由中点坐标公式得 所以点P1的坐标
为(-1,-3,2).(2)点P关于x轴的对称点P2的坐标;(3)点P关于坐标平面yOz的对称点P3的坐标.题型三空间两点间的距离【例3-1】 在空间直角坐标系中,给定点M(2,-1,3),若点A与点M关于xOy平面对称,点B与点M关于x轴对称,则|AB|等于( )
(A)2 (B)4
(C)2 (D)3【3-2】 已知点A(1,1,0),对于Oz轴正半轴上任意一点P,在Oy轴上是否存在一点B,使得PA⊥AB成立?若存在,求出B点的坐标;若不存在,说明理由.方法技巧 求空间两点间的距离时,一般使用空间两点间的距离公式,应用公式的关键在于建立适当的坐标系,确定两点的坐标.确定点的坐标的方法视具体题目而定,一般说来,要转化到平面中求解,有时也利用几何图形的特征,结合平面直角坐标系的知识确定.即时训练3-1:(1)在空间直角坐标系中,A(-6,0,1),B(-5,1,3),则|AB|=
;?
(2)若点P在x轴上,它到P1(0, ,3)的距离是到P2(0,1,-1)的距离的2倍,则点P的坐标为 ;?答案:(1) (2)(1,0,0)或(-1,0,0) 答案:(1)
4.3.1 空间直角坐标系
4.3.2 空间两点间的距离公式课标要求:1.理解空间直角坐标系的有关概念,会根据坐标描出点的位置、由点的位置写出点的坐标.2.掌握空间两点间的距离公式,理解公式使用的条件,会用公式计算或证明.自主学习知识探究1.空间直角坐标系的有关概念
如图,为了确定空间点的位置,我们建立空间直角坐标系.以单位正方体为截体.以O为原点,分别以射线OA,OC,OD′的方向为正方向,以线段OA,OC,OD′的长为单位长,建立三条数轴:x轴、y轴、z轴.这时,我们说建立了一个空间直角坐标系O-xyz,其中点O叫坐标原点,x轴、y轴、z轴叫坐标轴,通过每两个坐标轴的平面叫坐标平面,分别称为xOy平面、yOz平面、zOx平面,通常建立的坐标系为右手直角坐标系,即右手拇指指向x轴的正方向,食指指向y轴的正方向,中指指向z轴的正方向.2.空间任意点与有序数组(x,y,z)之间的对应法则
(1)过点P作一个平面平行于平面yOz(这样构造的平面同样垂直于x轴),这个平面与x轴的交点记为Px,它在x轴上的坐标为x,这个数x就叫做点P的x坐标或横坐标.
(2)过点P作一个平面平行于平面xOz(垂直于y轴),这个平面与y轴的交点记作Py,它在y轴上的坐标为y,这个数y叫做点P的y坐标或纵坐标.
(3)过点P作一个平面平行于平面xOy(垂直于z轴),这个平面与z轴的交点记作Pz,它在z轴上的坐标为z,这个数z叫做点P的z坐标或竖坐标.(3)关于点对称
点A关于点P的对称点为B?AB的中点为P,所以欲求点A关于点P的对称点,只需利用空间两点的中点坐标公式列方程求解即可.特别地,点A(x,y,z)关于原点的对称点为B(-x,-y,-z).自我检测(教师备用)1.点(0,2,1)位于( )
(A)y轴上 (B)z轴上
(C)xOy面上 (D)yOz面上DDA4.点P(-3,2,-1)关于平面xOy的对称点是 .?答案:(-3,2,1)5.设A(3,3,1),B(1,0,5),C(0,1,0),则AB的中点M到点C的距离|CM|= .?答案:题型一 空间中点的坐标的确定【例1】 如图所示,已知四棱锥P-ABCD,PB⊥AD,侧面PAD为边长等于2的等边三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°,G是棱PB的中点,请建立适当的空间直角坐标系,求出点P,A,B,C,D,G的坐标.课堂探究解:如图所示,过点P作PO⊥平面ABCD,垂足为点O.连接PE.因为AD⊥PB,
PO⊥AD,PO∩PB=P,
所以AD⊥平面POB,
所以AD⊥OB.因为PA=PD,所以OA=OD.
于是OB平分AD,点E为AD的中点,
所以PE⊥AD.
所以以垂足O为原点,以OB,OP及在底面ABCD内过O且垂直于OB的直线分别为y轴、z轴、x轴建立如图所示的空间直角坐标系.
由题意可得∠PEB=120°,∠PEO=180°-120°=60°.
又等边三角形PAD的边长等于2,
所以AE=ED=1,PE= .方法技巧 (1)建立空间直角坐标系时,要考虑如何建系才能使点的坐标简单、便于计算,一般是要使尽量多的点落在坐标轴上.
(2)对于长方体或正方体,一般取相邻的三条棱为x,y,z轴建立空间直角坐标系;确定点的坐标时,最常用的方法就是求某些与轴平行的线段的长度,即将坐标转化为与轴平行的线段长度,同时要注意坐标的符号,这也是求空间点的坐标的关键.即时训练1-1:如图,在长方体ABCD-A1B1C1D1中,E,F分别是棱BC,CC1上的点,
|CF|=|AB|=2|CE|,|AB|∶|AD|∶|AA1|=1∶2∶4.试建立适当的坐标系,写出E,F点的坐标.1-2:如图,长方体ABCD-A1B1C1D1中,|AB|=4,|AD|=3,|AA1|=5,N为棱CC1的中点,分别以AB,AD,AA1所在的直线为x,y,z轴,建立空间直角坐标系.
(1)求点A,B,C,D,A1,B1,C1,D1的坐标;解:(1)很明显A(0,0,0),
由于点B在x轴的正半轴上,且|OB|=4,所以B(4,0,0).同理,可得D(0,3,0),
A1(0,0,5).由于点C在坐标平面xOy内,BC⊥AB,CD⊥AD,则点C(4,3,0).
同理,可得B1(4,0,5),D1(0,3,5),与C的坐标相比,点C1的坐标中只有竖坐标不同,CC1=AA1=5,则点C1(4,3,5).(2)求点N的坐标.1-3:已知如图所示,在四棱锥P-ABCD中,四边形ABCD为正方形,PA⊥平面ABCD,且|PA|=|AB|=2,E为PD的中点.建立适当的坐标系,求A,B,C,D,P,E的坐标.解:如图所示,以A为坐标原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
由|PA|=|AB|=2,四边形ABCD为正方形,可知A,B,C,D,P,E的坐标分别为A(0,0,0,),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(0,1,1).题型二 空间直角坐标系中点的对称问题【例2】 已知点P(2,3,-1),求:
(1)点P关于各坐标平面对称的点的坐标;规范解答:(1)设点P关于xOy坐标平面的对称点为P′,则点P′在x轴上的坐标及在y轴上的坐标与点P在x轴上的坐标及在y轴上的坐标相同,而点P′在z轴上的坐标与点P在z轴上的坐标互为相反数.
所以,点P关于xOy坐标平面的对称点P′的坐标为(2,3,1).
同理,点P关于yOz,zOx坐标平面的对称点的坐标分别为(-2,3,-1),(2,
-3,-1).(2)点P关于各坐标轴对称的点的坐标;
(3)点P关于坐标原点对称的点的坐标.规范解答:(2)设点P关于x轴的对称点为Q,则点Q在x轴上的坐标与点P在x轴上的坐标相同,而点Q在y轴上的坐标及在z轴上的坐标与点P在y轴上的坐标及在z轴上的坐标互为相反数.
所以,点P关于x轴的对称点Q的坐标为(2,-3,1).
同理,点P关于y轴、z轴的对称点的坐标分别为(-2,3,1),(-2,-3,-1).
(3)点P(2,3,-1)关于坐标原点对称的点的坐标为(-2,-3,1).(4)点P关于点(1,2,-6)对称的点的坐标.即时训练2-1:(1)在空间直角坐标系中,点P(3,4,5)与点Q(3,-4,-5)两点的位置关系是( )
(A)关于x轴对称 (B)关于xOy平面对称
(C)关于坐标原点对称 (D)以上都不对
(2)在空间直角坐标系中,点P(-2,1,4)关于xOy平面对称的点的坐标是( )
(A)(-2,1,-4) (B)(-2,-1,-4)
(C)(2,-1,4) (D)(2,1,-4)解析:(1)由于P,Q两点的横坐标相等,纵坐标与竖坐标分别互为相反数,故P,Q两点关于x轴对称.故选A.
(2)过点P向xOy平面作垂线,垂足为N,则N就是点P与它关于xOy平面的对称点的中点,因为N的坐标为(-2,1,0),所以对称点的坐标为(-2,1,-4),故选A.2-2:在空间直角坐标系中有一个点P(1,3,-2),求:
(1)点P关于坐标原点O的对称点P1的坐标;解:(1)设点P1的坐标为(x1,y1,z1),因为点P和P1关于坐标原点O对称,所
以点O为线段PP1的中点,由中点坐标公式得 所以点P1的坐标
为(-1,-3,2).(2)点P关于x轴的对称点P2的坐标;(3)点P关于坐标平面yOz的对称点P3的坐标.题型三空间两点间的距离【例3-1】 在空间直角坐标系中,给定点M(2,-1,3),若点A与点M关于xOy平面对称,点B与点M关于x轴对称,则|AB|等于( )
(A)2 (B)4
(C)2 (D)3【3-2】 已知点A(1,1,0),对于Oz轴正半轴上任意一点P,在Oy轴上是否存在一点B,使得PA⊥AB成立?若存在,求出B点的坐标;若不存在,说明理由.方法技巧 求空间两点间的距离时,一般使用空间两点间的距离公式,应用公式的关键在于建立适当的坐标系,确定两点的坐标.确定点的坐标的方法视具体题目而定,一般说来,要转化到平面中求解,有时也利用几何图形的特征,结合平面直角坐标系的知识确定.即时训练3-1:(1)在空间直角坐标系中,A(-6,0,1),B(-5,1,3),则|AB|=
;?
(2)若点P在x轴上,它到P1(0, ,3)的距离是到P2(0,1,-1)的距离的2倍,则点P的坐标为 ;?答案:(1) (2)(1,0,0)或(-1,0,0) 答案:(1)
