高中数学新人教A版必修2课件:第一章空间几何体1.2.1中心投影与平行投影1.2.2空间几何体的三视图(28张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第一章空间几何体1.2.1中心投影与平行投影1.2.2空间几何体的三视图(28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 17:02:16 | ||
图片预览




文档简介
课件28张PPT。1.2 空间几何体的三视图和直观图
1.2.1 中心投影与平行投影
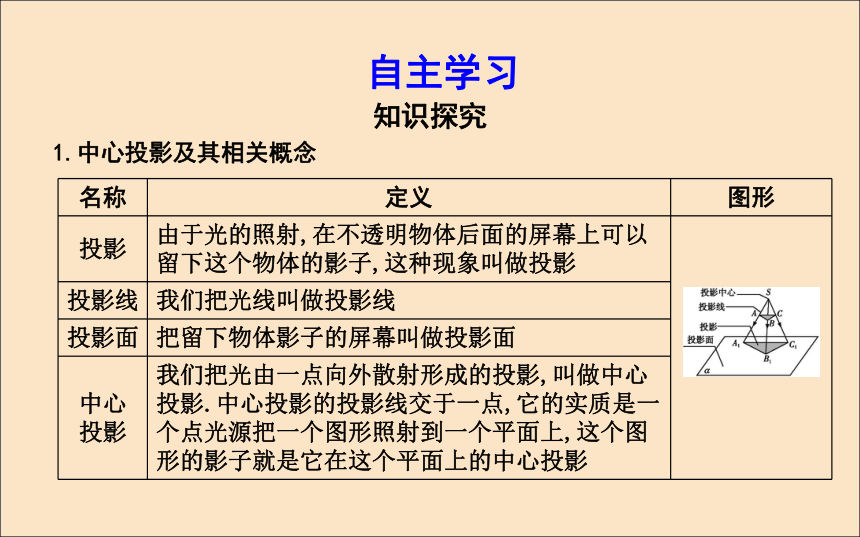
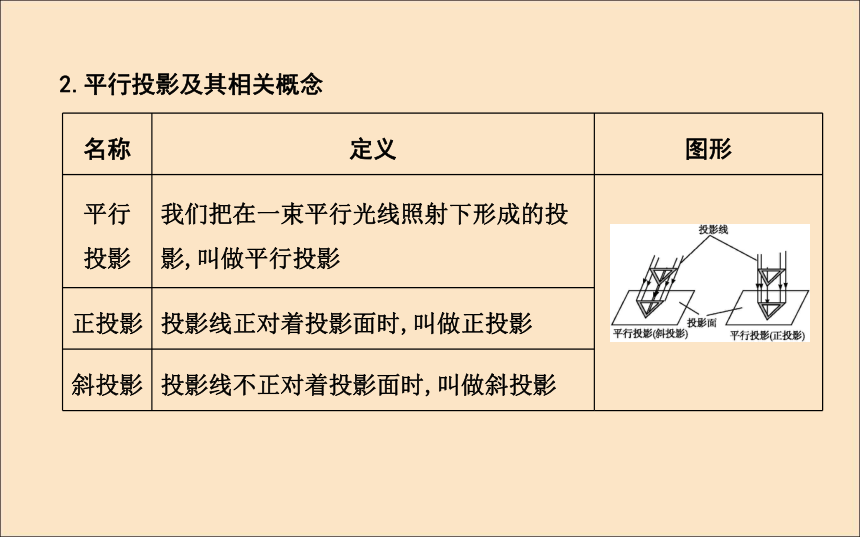
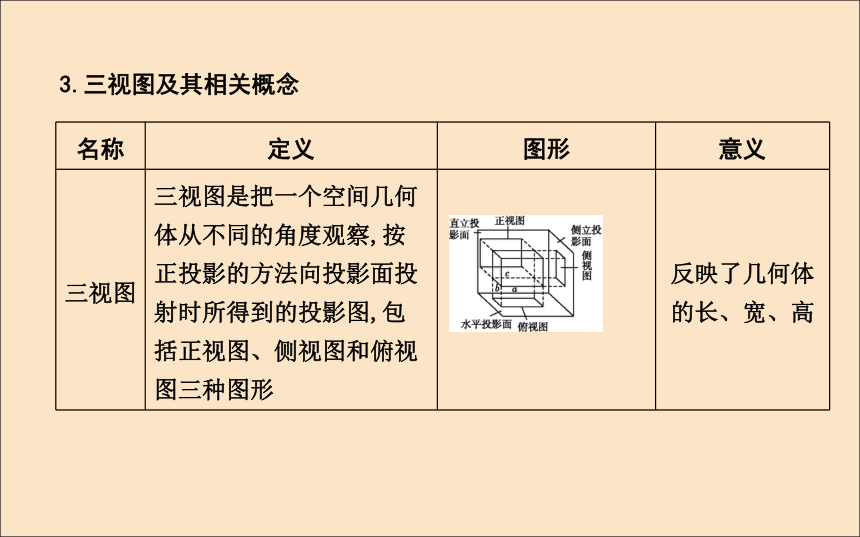
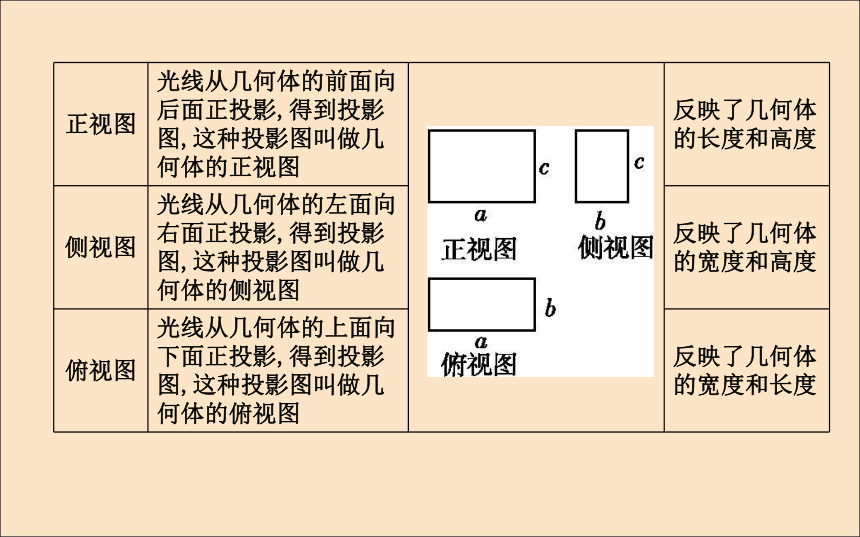
1.2.2 空间几何体的三视图课标要求:1.了解中心投影与平行投影.2.能画出简单的空间图形(柱、锥、台、球及其组合体)的三视图.3.能识别三视图所表示的立体模型.自主学习知识探究1.中心投影及其相关概念2.平行投影及其相关概念3.三视图及其相关概念4.简单组合体的三视图
画组合体的三视图的一般步骤如下:
(1)形体分析:组合体比基本几何体复杂,但它来源于基本几何体,只需先分析组合形式,把组合体分解为基本几何体,再按一个一个基本几何体画图,就可以画出组合体的三视图.
(2)选出正视图:摆放组合体,应选择最能反映组合体形状特征的方向为正视图的投影方向,其他视图就按正视图投影关系画出.
(3)确定画图步骤:一般先画出各视图的主要对应元素,按先整体后局部的顺序进行.自我检测(教师备用)1.已知△ABC,选定的投影面与△ABC所在的平面平行,则经过中心投影后(投影线与投影面相交)所得的三角形与△ABC( )
(A)全等 (B)相似
(C)不相似 (D)以上均有可能
2.在三棱锥、正方体、长方体、圆柱、圆锥、圆台、球中,正视图、俯视图、侧视图都相同的几何体有( )
(A)1个 (B)2个
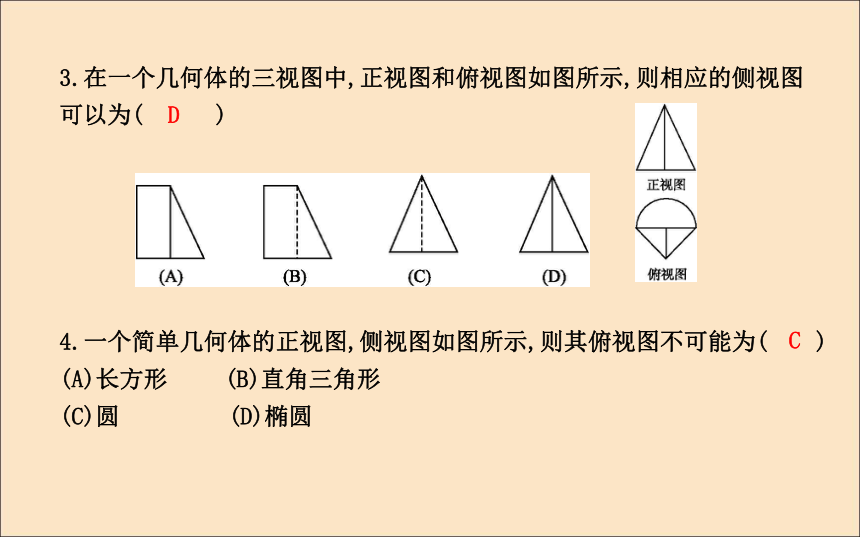
(C)3个 (D)4个B B 3.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为( )D 4.一个简单几何体的正视图,侧视图如图所示,则其俯视图不可能为( )
(A)长方形 (B)直角三角形
(C)圆 (D)椭圆C 5.有一个几何体的三视图如图所示,这个几何体应是一个( )
(A)棱台 (B)棱锥
(C)棱柱 (D)正四面体答案:9π 4A 题型一 简单几何体的三视图【例1-1】 画出如图所示的正三棱柱、正四棱锥和正五棱台的三视图.课堂探究解:如图几何体对应的三视图分别为
(1),(2),(3)图所示.【1-2】 如图,画出四面体AB1CD1的正视图,则得到的正视图可以为( )解析:根据投影及正视图的概念,可知A符合.故选A.方法技巧 画几何体的三视图时需注意的问题
(1)确定正视的方向,同一物体观察的角度不同,所画的三视图可能不同;
(2)注意辨析分界线,以及轮廓线的实与虚;
(3)正确摆放三个视图的位置.即时训练1-1:(1)定义:底面是正三角形,侧棱与底面垂直的三棱柱叫做正三棱柱.将正三棱柱截去一个角(如图1所示,M,N分别是AB,BC的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图为( )解析:(1)N的投影是C,M的投影是AC的中点.对照各图.选D.答案:(1)D(2)一个几何体的三视图如图所示,则俯视图的面积是 .?解析:(2)由题意得a× = ,所以a=2.
所以俯视图的面积S=3×2=6.答案:(2)61-2:三棱锥D-ABC及其三视图中的正视图和侧视图如图所示,则棱BD的长为 .?题型二 简单组合体的三视图【例2-1】 如图,设所给的方向为物体的正前方,试画出它的三视图.(单位:cm)解:三视图如图:【2-2】 如图所示的是由几个小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置上小正方体的个数.请画出该几何体的正视图和侧视图,并在其上标出小正方体的个数,求出所有小正方体的个数.解:可先根据几何体的俯视图、小正方体的个数想象或画出几何体,再根据几何体的结构特征画出其正视图及侧视图.
正视图及侧视图如图所示.小正方体的个数为1+2+4+3+2=12.方法技巧 画简单组合体的三视图,首先确定组合体的组成形式,然后确定每个组成部分,最后画出三视图.若相邻两个几何体的表面相交,表面的交线是它们的分界线,在三视图中,要将分界线按虚(或实)线画出.即时训练2-1:一根钢管如图所示,则它的三视图为( )解析:该几何体是由圆柱中挖去一个圆柱形成的几何体,三视图为B.2-2:如图,在正方体ABCD-A1B1C1D1中,E为棱BB1的中点,用过点A,E,C1的平面截去该正方体的上部分,则剩余几何体的正视图为( )解析:设过点A,E,C1的截面与棱DD1相交于点F,则F是棱DD1的中点,截去正方体的上部分,剩余几何体的直观图如图所示,则其正视图为C.故选C.题型三由三视图还原几何体【例3-1】 如图所示为一个简单几何体的三视图,则其对应的实物图是( )解析:根据三种视图的对角线的位置,可以判断A是正确的.故选A.变式探究:本例中三视图对应的几何体是一个什么样的组合体?解:因为实物图为A,所以该几何体是由一个直三棱柱和一个四棱锥组成的.【3-2】 某多面体的三视图如图所示,其中正视图和侧视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )(A)10 (B)12
(C)14 (D)16方法技巧 (1)根据三视图还原几何体,要仔细分析和认真观察三视图并进行充分的想象,然后综合三视图的形状,从不同的角度去还原.(2)通常要根据俯视图判断几何体是多面体还是旋转体,再结合正视图和侧视图确定具体的几何结构特征,最终确定是简单几何体还是简单组合体.即时训练3-1:如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则这个几何体是( )
(A)三棱锥 (B)三棱柱
(C)四棱锥 (D)四棱柱解析:构造棱长为4的正方体,由三视图,可知该几何体为如图所示的三棱锥P-ABC,其中点P,B分别为相应棱的中点,故选A.3-2:已知某几何体的正视图和侧视图均为如图所示的图形,给出下列图形:解析:结合题中所给俯视图,可知几何体可以为圆柱挖去一个小圆柱,圆柱挖去正方体,正方体挖去圆柱,正方体挖去底面为等腰直角三角形的直三棱柱等,所以①②③⑤都可作为俯视图.几何体不可能是正方体挖去一个底面为等边三角形的直三棱柱,故④不可能.故选B.其中可以作为该几何体的俯视图的图形个数是( )
(A)5 (B)4 (C)3 (D)23-3:某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )解析:该几何体是底面为正方形,一侧棱垂直于底面的四棱锥,最长棱的棱长为 = ,故选C.(A)1 (B) (C) (D)2
1.2.1 中心投影与平行投影
1.2.2 空间几何体的三视图课标要求:1.了解中心投影与平行投影.2.能画出简单的空间图形(柱、锥、台、球及其组合体)的三视图.3.能识别三视图所表示的立体模型.自主学习知识探究1.中心投影及其相关概念2.平行投影及其相关概念3.三视图及其相关概念4.简单组合体的三视图
画组合体的三视图的一般步骤如下:
(1)形体分析:组合体比基本几何体复杂,但它来源于基本几何体,只需先分析组合形式,把组合体分解为基本几何体,再按一个一个基本几何体画图,就可以画出组合体的三视图.
(2)选出正视图:摆放组合体,应选择最能反映组合体形状特征的方向为正视图的投影方向,其他视图就按正视图投影关系画出.
(3)确定画图步骤:一般先画出各视图的主要对应元素,按先整体后局部的顺序进行.自我检测(教师备用)1.已知△ABC,选定的投影面与△ABC所在的平面平行,则经过中心投影后(投影线与投影面相交)所得的三角形与△ABC( )
(A)全等 (B)相似
(C)不相似 (D)以上均有可能
2.在三棱锥、正方体、长方体、圆柱、圆锥、圆台、球中,正视图、俯视图、侧视图都相同的几何体有( )
(A)1个 (B)2个
(C)3个 (D)4个B B 3.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为( )D 4.一个简单几何体的正视图,侧视图如图所示,则其俯视图不可能为( )
(A)长方形 (B)直角三角形
(C)圆 (D)椭圆C 5.有一个几何体的三视图如图所示,这个几何体应是一个( )
(A)棱台 (B)棱锥
(C)棱柱 (D)正四面体答案:9π 4A 题型一 简单几何体的三视图【例1-1】 画出如图所示的正三棱柱、正四棱锥和正五棱台的三视图.课堂探究解:如图几何体对应的三视图分别为
(1),(2),(3)图所示.【1-2】 如图,画出四面体AB1CD1的正视图,则得到的正视图可以为( )解析:根据投影及正视图的概念,可知A符合.故选A.方法技巧 画几何体的三视图时需注意的问题
(1)确定正视的方向,同一物体观察的角度不同,所画的三视图可能不同;
(2)注意辨析分界线,以及轮廓线的实与虚;
(3)正确摆放三个视图的位置.即时训练1-1:(1)定义:底面是正三角形,侧棱与底面垂直的三棱柱叫做正三棱柱.将正三棱柱截去一个角(如图1所示,M,N分别是AB,BC的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图为( )解析:(1)N的投影是C,M的投影是AC的中点.对照各图.选D.答案:(1)D(2)一个几何体的三视图如图所示,则俯视图的面积是 .?解析:(2)由题意得a× = ,所以a=2.
所以俯视图的面积S=3×2=6.答案:(2)61-2:三棱锥D-ABC及其三视图中的正视图和侧视图如图所示,则棱BD的长为 .?题型二 简单组合体的三视图【例2-1】 如图,设所给的方向为物体的正前方,试画出它的三视图.(单位:cm)解:三视图如图:【2-2】 如图所示的是由几个小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置上小正方体的个数.请画出该几何体的正视图和侧视图,并在其上标出小正方体的个数,求出所有小正方体的个数.解:可先根据几何体的俯视图、小正方体的个数想象或画出几何体,再根据几何体的结构特征画出其正视图及侧视图.
正视图及侧视图如图所示.小正方体的个数为1+2+4+3+2=12.方法技巧 画简单组合体的三视图,首先确定组合体的组成形式,然后确定每个组成部分,最后画出三视图.若相邻两个几何体的表面相交,表面的交线是它们的分界线,在三视图中,要将分界线按虚(或实)线画出.即时训练2-1:一根钢管如图所示,则它的三视图为( )解析:该几何体是由圆柱中挖去一个圆柱形成的几何体,三视图为B.2-2:如图,在正方体ABCD-A1B1C1D1中,E为棱BB1的中点,用过点A,E,C1的平面截去该正方体的上部分,则剩余几何体的正视图为( )解析:设过点A,E,C1的截面与棱DD1相交于点F,则F是棱DD1的中点,截去正方体的上部分,剩余几何体的直观图如图所示,则其正视图为C.故选C.题型三由三视图还原几何体【例3-1】 如图所示为一个简单几何体的三视图,则其对应的实物图是( )解析:根据三种视图的对角线的位置,可以判断A是正确的.故选A.变式探究:本例中三视图对应的几何体是一个什么样的组合体?解:因为实物图为A,所以该几何体是由一个直三棱柱和一个四棱锥组成的.【3-2】 某多面体的三视图如图所示,其中正视图和侧视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )(A)10 (B)12
(C)14 (D)16方法技巧 (1)根据三视图还原几何体,要仔细分析和认真观察三视图并进行充分的想象,然后综合三视图的形状,从不同的角度去还原.(2)通常要根据俯视图判断几何体是多面体还是旋转体,再结合正视图和侧视图确定具体的几何结构特征,最终确定是简单几何体还是简单组合体.即时训练3-1:如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则这个几何体是( )
(A)三棱锥 (B)三棱柱
(C)四棱锥 (D)四棱柱解析:构造棱长为4的正方体,由三视图,可知该几何体为如图所示的三棱锥P-ABC,其中点P,B分别为相应棱的中点,故选A.3-2:已知某几何体的正视图和侧视图均为如图所示的图形,给出下列图形:解析:结合题中所给俯视图,可知几何体可以为圆柱挖去一个小圆柱,圆柱挖去正方体,正方体挖去圆柱,正方体挖去底面为等腰直角三角形的直三棱柱等,所以①②③⑤都可作为俯视图.几何体不可能是正方体挖去一个底面为等边三角形的直三棱柱,故④不可能.故选B.其中可以作为该几何体的俯视图的图形个数是( )
(A)5 (B)4 (C)3 (D)23-3:某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )解析:该几何体是底面为正方形,一侧棱垂直于底面的四棱锥,最长棱的棱长为 = ,故选C.(A)1 (B) (C) (D)2
