高中数学新人教A版必修2课件:第一章空间几何体1.2.3空间几何体的直观图(24张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第一章空间几何体1.2.3空间几何体的直观图(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 17:03:35 | ||
图片预览







文档简介
课件24张PPT。1.2.3 空间几何体的直观图课标要求:1.了解斜二测画法的概念并掌握斜二测画法的步骤.2.会用斜二测画法画出一些简单平面图形和立体图形的直观图.3.强化三视图、直观图、原空间几何体形状之间的相互转换.自主学习知识探究1.直观图定义
当投射线和投射面成适当的角度或改变图形相对于投射面的位置时,一个空间图形在投射面上的平行投影(平面图形)可以形象地表示这个空间图形.像这样用来表示空间图形的平面图形,叫做空间图形的直观图.2.平面图形直观图的斜二测画法步骤注意:斜二测画法的直观图与原图的面积关系
一个平面多边形的面积为S原,它的斜二测画法直观图的面积为S直,则有S直=
S原.3.空间几何体的直观图的画法自我检测(教师备用)1.下列说法中正确的是( )
(A)互相垂直的两条直线的直观图仍然是两条互相垂直的直线
(B)梯形的直观图可能是平行四边形
(C)矩形的直观图可能是梯形
(D)正方形的直观图可能是平行四边形
2.如图所示的水平放置的平面图形的直观图,所表示的图形ABCD是( )
(A)任意梯形
(B)直角梯形
(C)任意四边形
(D)平行四边形D B 3.若AB=2CD,AB∥x轴,CD∥y轴,在直观图中,AB的直观图为A′B′,CD的直观图为C′D′,则( )
(A)A′B′=2C′D′ (B)A′B′=C′D′
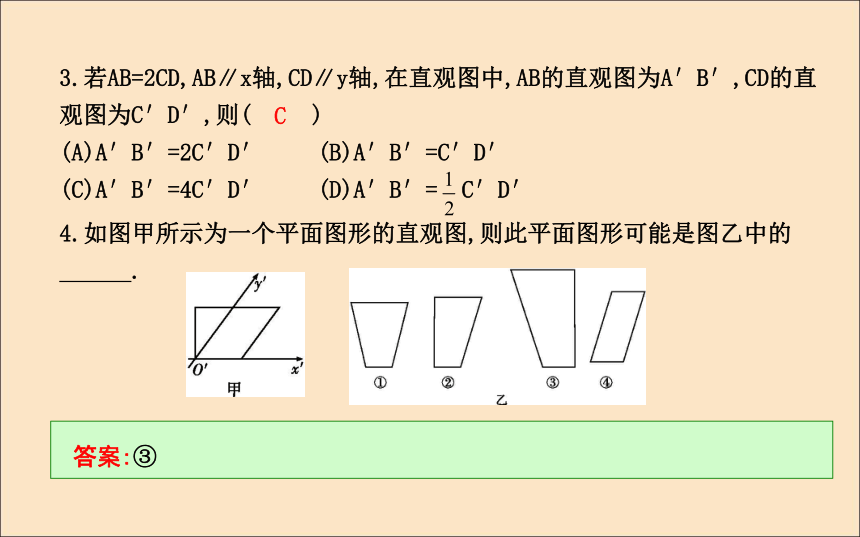
(C)A′B′=4C′D′ (D)A′B′= C′D′C 答案:③4.如图甲所示为一个平面图形的直观图,则此平面图形可能是图乙中的
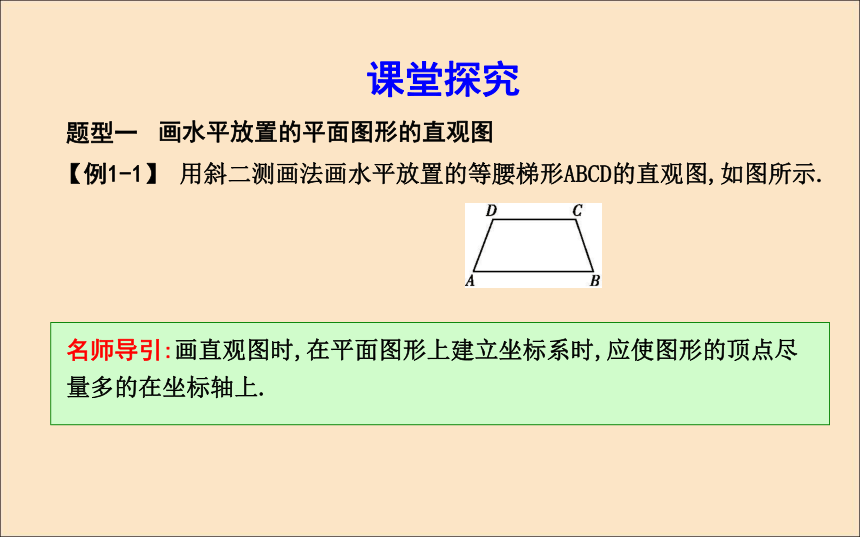
.?5.已知正方形的直观图是有一条边长为4的平行四边形,则此正方形的面积为 .?答案:16或64题型一 画水平放置的平面图形的直观图【例1-1】 用斜二测画法画水平放置的等腰梯形ABCD的直观图,如图所示.课堂探究名师导引:画直观图时,在平面图形上建立坐标系时,应使图形的顶点尽量多的在坐标轴上.解:画法:(1)如图所示,取AB所在直线为x轴,AB中点O为原点,建立直角坐标系,画对应的坐标系x′O′y′,使∠x′O′y′=45°.(2)以 O′为中点在x′轴上取A′B′=AB,在y′轴上取O′E′= OE,以E′为中点画C′D′∥x′轴,并使C′D′=CD.(3)连接B′C′,D′A′,所得的四边形A′B′C′D′就是水平放置的等腰梯形ABCD的直观图.【1-2】 若(1)中已知原梯形上底DC=1,下底AB=3,高为2,求直观图的面积?解:由水平放置的直观图的作法可知四边形A′B′C′D′仍为梯形,其中A′B′=3,C′D′=1,
高h′=O′E′sin 45°=1× = ,
所以S梯形A′B′C′D′= = = .方法技巧 画水平放置的平面图形的直观图的关键及注意点:画图的关键是确定顶点的位置,画图时要注意原图和直观图中线段的长度关系是否发生改变.即时训练1-1:利用斜二测画法得到:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形.以上结论中,正确的是 (填序号).?解析:由直观图的画法可知,三角形的直观图是三角形,平行四边形的直观图是平行四边形,正方形的直观图不是正方形,菱形的直观图不是菱形,故正确的是①②.答案:①②1-2:已知正△ABC的边长为a,那么正△ABC用斜二测画法得到的直观图△A′B′C′的面积是( )题型二 画空间几何体的直观图【例2-1】 有一个正六棱锥(底面为正六边形,侧面为全等的等腰三角形的棱锥),底面边长为3 cm,高为5 cm,画出这个正六棱锥的直观图.解:(1)先画出边长为3 cm的正六边形水平放置的直观图,如图①所示.
(2)过正六边形的中心O′建立z′轴,画出正六棱锥的顶点V′,如图②所示.
(3)连接V′A′,V′B′,V′C′,V′D′,V′E′,V′F′,如图③所示.
(4)擦去辅助线,遮挡部分用虚线表示,即得到正六棱锥的直观图,如图④所示.【2-2】 某几何体的三视图如图所示,用斜二测画法画出它的直观图.解:(1)画轴.如图①,画x轴,y轴,z轴,使∠xOy=45°,∠xOz=90°.
(2)画圆台的两底面,利用斜二测画法,画出底面☉O,在z轴上截取OO′,使OO′等于三视图中相应的高度,过点O′作Ox的平行线O′x′,作Oy的平行线O′y′,利用O′x′与O′y′画出上底面☉O′.
(3)画圆锥的顶点.在Oz上取点P,使PO′等于三视图中相应的高度.
(4)成图.连接PA′,PB′,A′A,B′B,整理得到三视图
表示的几何体的直观图,如图②.方法技巧 (1)画空间几何体的直观图,可先画出底面的平面图形,然后画出竖轴.此外,坐标系的建立要充分利用图形的对称性,以便方便、准确地确定顶点;
(2)对于一些常见几何体(如柱、锥、台、球)的直观图,应该记住它们的大致形状,以便可以又快又准的画出.即时训练2-1:由下列几何体的三视图画出直观图.解:(1)画轴.
如图,画出x轴、y轴、z轴,三轴相交于点O,
使∠xOy=45°,∠xOz=90°.
(2)画底面.作水平放置的三角形(俯视图)的直观图△ABC.
(3)画侧棱.过A、B、C各点分别作z轴的平行线,并在这些平行线上分别截取线段AA′=BB′=CC′,且都与正视图或侧视图的高相等.
(4)成图.顺次连接A′、B′、C′,并加以整理(擦去辅助线,将遮挡部分用虚线表示),得到的图形就是所求的几何体的直观图.2-2:如图所示,由下列几何体的三视图画出它的直观图.解:(1)画轴.画x′轴、y′轴和z′轴,使∠x′O′y′=45°(或135°),∠x′O′z′=90°,如图①所示.(2)画底面.按x′轴、y′轴画正五边形的直观图ABCDE.
(3)画侧棱.过点A,B,C,D,E分别作z′轴的平行线,并在这些平行线上分别截取AA′,BB′,CC′,DD′,EE′都等于正视图的高.
(4)成图.顺次连接A′,B′,C′,D′,E′,去掉辅助线,改被挡部分虚线,如图②所示.题型三 直观图还原为平面图形【例3-1】 (10分)如图是一梯形OABC的直观图,其直观图面积为S,求梯形OABC的面积.规范解答:设O′C′=h,
则原梯形是一个直角梯形且高为2h.
C′B′=CB,O′A′=OA. …………………………2分
过C′作C′D⊥O′A′于D,【3-2】 如例题图所示,若在O′A′上取点D′,且梯形A′B′C′D′的面积是S,求梯形ABCD的面积.方法技巧 (1)还原图形的过程是画直观图的逆过程,关键是找与x′轴、y′轴平行的直线或线段.平行于x′轴的线段长度不变,平行于y′轴的线段还原时长度变为原来的2倍,由此确定图形的各个顶点,顺次连接即可.(2)求图形的面积,关键是能先正确画出图形,然后求出相应边的长度,利用公式求解.
(3)原图的面积S与直观图的面积S′之间的关系为S=2 S′.即时训练3-1:一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′,如图若O′B′=1,那么原△ABO的面积与直观图的面积之比为 .?3-2:如图所示,正方形O′A′B′C′的边长为1 cm,它是水平放置的一个平面图形的直观图,求原图形的周长.
当投射线和投射面成适当的角度或改变图形相对于投射面的位置时,一个空间图形在投射面上的平行投影(平面图形)可以形象地表示这个空间图形.像这样用来表示空间图形的平面图形,叫做空间图形的直观图.2.平面图形直观图的斜二测画法步骤注意:斜二测画法的直观图与原图的面积关系
一个平面多边形的面积为S原,它的斜二测画法直观图的面积为S直,则有S直=
S原.3.空间几何体的直观图的画法自我检测(教师备用)1.下列说法中正确的是( )
(A)互相垂直的两条直线的直观图仍然是两条互相垂直的直线
(B)梯形的直观图可能是平行四边形
(C)矩形的直观图可能是梯形
(D)正方形的直观图可能是平行四边形
2.如图所示的水平放置的平面图形的直观图,所表示的图形ABCD是( )
(A)任意梯形
(B)直角梯形
(C)任意四边形
(D)平行四边形D B 3.若AB=2CD,AB∥x轴,CD∥y轴,在直观图中,AB的直观图为A′B′,CD的直观图为C′D′,则( )
(A)A′B′=2C′D′ (B)A′B′=C′D′
(C)A′B′=4C′D′ (D)A′B′= C′D′C 答案:③4.如图甲所示为一个平面图形的直观图,则此平面图形可能是图乙中的
.?5.已知正方形的直观图是有一条边长为4的平行四边形,则此正方形的面积为 .?答案:16或64题型一 画水平放置的平面图形的直观图【例1-1】 用斜二测画法画水平放置的等腰梯形ABCD的直观图,如图所示.课堂探究名师导引:画直观图时,在平面图形上建立坐标系时,应使图形的顶点尽量多的在坐标轴上.解:画法:(1)如图所示,取AB所在直线为x轴,AB中点O为原点,建立直角坐标系,画对应的坐标系x′O′y′,使∠x′O′y′=45°.(2)以 O′为中点在x′轴上取A′B′=AB,在y′轴上取O′E′= OE,以E′为中点画C′D′∥x′轴,并使C′D′=CD.(3)连接B′C′,D′A′,所得的四边形A′B′C′D′就是水平放置的等腰梯形ABCD的直观图.【1-2】 若(1)中已知原梯形上底DC=1,下底AB=3,高为2,求直观图的面积?解:由水平放置的直观图的作法可知四边形A′B′C′D′仍为梯形,其中A′B′=3,C′D′=1,
高h′=O′E′sin 45°=1× = ,
所以S梯形A′B′C′D′= = = .方法技巧 画水平放置的平面图形的直观图的关键及注意点:画图的关键是确定顶点的位置,画图时要注意原图和直观图中线段的长度关系是否发生改变.即时训练1-1:利用斜二测画法得到:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形.以上结论中,正确的是 (填序号).?解析:由直观图的画法可知,三角形的直观图是三角形,平行四边形的直观图是平行四边形,正方形的直观图不是正方形,菱形的直观图不是菱形,故正确的是①②.答案:①②1-2:已知正△ABC的边长为a,那么正△ABC用斜二测画法得到的直观图△A′B′C′的面积是( )题型二 画空间几何体的直观图【例2-1】 有一个正六棱锥(底面为正六边形,侧面为全等的等腰三角形的棱锥),底面边长为3 cm,高为5 cm,画出这个正六棱锥的直观图.解:(1)先画出边长为3 cm的正六边形水平放置的直观图,如图①所示.
(2)过正六边形的中心O′建立z′轴,画出正六棱锥的顶点V′,如图②所示.
(3)连接V′A′,V′B′,V′C′,V′D′,V′E′,V′F′,如图③所示.
(4)擦去辅助线,遮挡部分用虚线表示,即得到正六棱锥的直观图,如图④所示.【2-2】 某几何体的三视图如图所示,用斜二测画法画出它的直观图.解:(1)画轴.如图①,画x轴,y轴,z轴,使∠xOy=45°,∠xOz=90°.
(2)画圆台的两底面,利用斜二测画法,画出底面☉O,在z轴上截取OO′,使OO′等于三视图中相应的高度,过点O′作Ox的平行线O′x′,作Oy的平行线O′y′,利用O′x′与O′y′画出上底面☉O′.
(3)画圆锥的顶点.在Oz上取点P,使PO′等于三视图中相应的高度.
(4)成图.连接PA′,PB′,A′A,B′B,整理得到三视图
表示的几何体的直观图,如图②.方法技巧 (1)画空间几何体的直观图,可先画出底面的平面图形,然后画出竖轴.此外,坐标系的建立要充分利用图形的对称性,以便方便、准确地确定顶点;
(2)对于一些常见几何体(如柱、锥、台、球)的直观图,应该记住它们的大致形状,以便可以又快又准的画出.即时训练2-1:由下列几何体的三视图画出直观图.解:(1)画轴.
如图,画出x轴、y轴、z轴,三轴相交于点O,
使∠xOy=45°,∠xOz=90°.
(2)画底面.作水平放置的三角形(俯视图)的直观图△ABC.
(3)画侧棱.过A、B、C各点分别作z轴的平行线,并在这些平行线上分别截取线段AA′=BB′=CC′,且都与正视图或侧视图的高相等.
(4)成图.顺次连接A′、B′、C′,并加以整理(擦去辅助线,将遮挡部分用虚线表示),得到的图形就是所求的几何体的直观图.2-2:如图所示,由下列几何体的三视图画出它的直观图.解:(1)画轴.画x′轴、y′轴和z′轴,使∠x′O′y′=45°(或135°),∠x′O′z′=90°,如图①所示.(2)画底面.按x′轴、y′轴画正五边形的直观图ABCDE.
(3)画侧棱.过点A,B,C,D,E分别作z′轴的平行线,并在这些平行线上分别截取AA′,BB′,CC′,DD′,EE′都等于正视图的高.
(4)成图.顺次连接A′,B′,C′,D′,E′,去掉辅助线,改被挡部分虚线,如图②所示.题型三 直观图还原为平面图形【例3-1】 (10分)如图是一梯形OABC的直观图,其直观图面积为S,求梯形OABC的面积.规范解答:设O′C′=h,
则原梯形是一个直角梯形且高为2h.
C′B′=CB,O′A′=OA. …………………………2分
过C′作C′D⊥O′A′于D,【3-2】 如例题图所示,若在O′A′上取点D′,且梯形A′B′C′D′的面积是S,求梯形ABCD的面积.方法技巧 (1)还原图形的过程是画直观图的逆过程,关键是找与x′轴、y′轴平行的直线或线段.平行于x′轴的线段长度不变,平行于y′轴的线段还原时长度变为原来的2倍,由此确定图形的各个顶点,顺次连接即可.(2)求图形的面积,关键是能先正确画出图形,然后求出相应边的长度,利用公式求解.
(3)原图的面积S与直观图的面积S′之间的关系为S=2 S′.即时训练3-1:一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′,如图若O′B′=1,那么原△ABO的面积与直观图的面积之比为 .?3-2:如图所示,正方形O′A′B′C′的边长为1 cm,它是水平放置的一个平面图形的直观图,求原图形的周长.
