高中数学新人教A版必修2课件:第一章空间几何体1.3.1柱体、锥体、台体的表面积与体积(27张ppt)
文档属性
| 名称 | 高中数学新人教A版必修2课件:第一章空间几何体1.3.1柱体、锥体、台体的表面积与体积(27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 00:00:00 | ||
图片预览







文档简介
课件27张PPT。1.3 空间几何体的表面积与体积
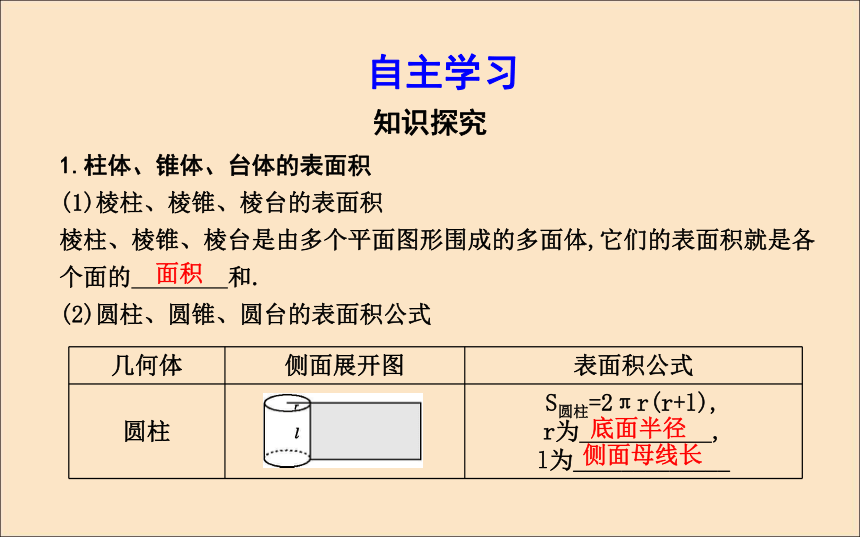
1.3.1 柱体、锥体、台体的表面积与体积课标要求:1.通过对柱、锥、台体的研究,掌握柱、锥、台体的表面积的求法.2.了解柱、锥、台体的表面积计算公式;能运用柱、锥、台的表面积公式进行计算和解决有关实际问题.3.培养空间想象能力和思维能力.自主学习知识探究1.柱体、锥体、台体的表面积
(1)棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台是由多个平面图形围成的多面体,它们的表面积就是各个面的 和.
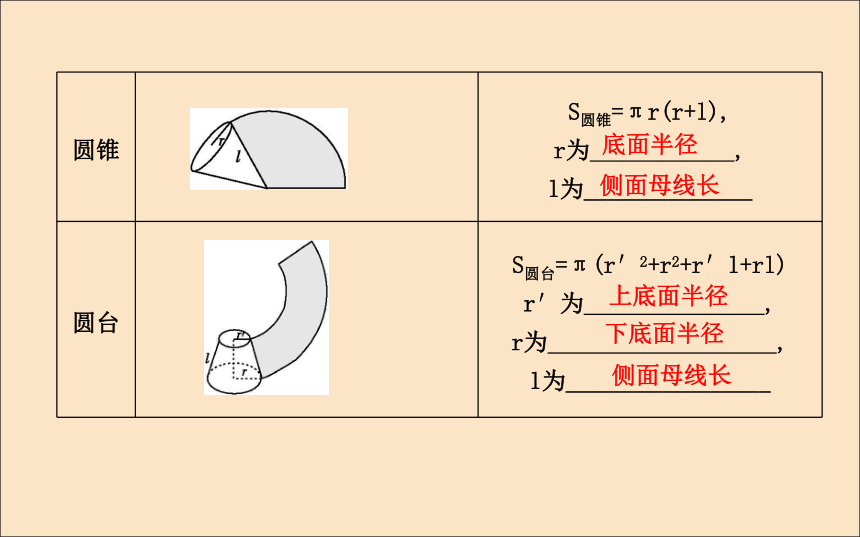
(2)圆柱、圆锥、圆台的表面积公式面积底面半径侧面母线长底面半径侧面母线长上底面半径下底面半径侧面母线长2.柱体、锥体与台体的体积公式底面积 高 底面积 高 上、下底面面积 高 自我检测(教师备用)1.已知圆锥的母线长为5,底面周长为6π,则它的体积为( )
(A)36π (B)30π
(C)24π (D)12πD 2.若圆台的高为4,母线长为5,侧面积为45π,则圆台的上、下底面的面积之和为( )
(A)9π (B)36π
(C)45π (D)81πC 3.已知一个几何体的三视图如图所示,则该几何体的体积为( )
(A)12π (B)8π
(C) (D)D 4.某四棱锥的三视图如图所示,则该四棱锥的表面积是( )B (A)32 (B)16+16
(C)48 (D)16+325.已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开扇形的圆心角为 .?答案:180°题型一 空间几何体的表面积【例1-1】 将圆心角为120°,面积为3π的扇形作为圆锥的侧面,则圆锥的表面积为 .?课堂探究答案:4π【1-2】 一个四面体的三视图如图所示,则该四面体的表面积是( )方法技巧 (1)多面体的表面积转化为各面面积之和.
(2)解决有关棱台的问题时,常用两种解题思路:一是把基本量转化到直角梯形中去解决;二是把棱台还原成棱锥,利用棱锥的有关知识来解决.
(3)旋转体中,求面积应注意侧面展开图,上下面圆的周长是展开图的弧长.圆台通常还要还原为圆锥.即时训练1-1:(1)圆柱的底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是( )
(A)4πS (B)2πS (C)πS (D) πS(2)一个几何体的三视图及尺寸如图所示,其中正视图、侧视图都是等腰三角形,俯视图是圆,则该几何体的表面积是( )
(A)12π (B)14π
(C)16π (D)28π题型二 空间几何体的体积【例2-1】 (12分)圆锥的轴截面是等腰直角三角形,侧面积是16 π,求圆锥的体积.【2-2】 如图,圆台高为3,轴截面中母线AA1与底面直径AB的夹角为60°,轴截面中一条对角线垂直于腰,求圆台的体积.方法技巧 (1)常见的求几何体体积的方法
①公式法:直接代入公式求解.
②等积法:如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可.
③分割法:将几何体分割成易求解的几部分,分别求体积.
(2)求几何体体积时需注意的问题
柱、锥、台的体积的计算,一般要找出相应的底面和高,要充分利用截面、轴截面,求出所需要的量,最后代入公式计算.即时训练2-1:一个几何体的三视图如图所示,则该几何体的体积为( )(A) (B)π
(C) (D)2π2-2:(1)在棱长为1的正方体上,分别用过共顶点的三条棱的中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是 .?(2)如图所示,梯形ABCD中,AD∥BC,∠ABC=90°,AD=a, BC=2a,∠DCB= 60°,在平面ABCD内过点C作l⊥CB,以l为轴旋转一周.求旋转体的表面积和体积.题型三组合体的表面积与体积【例3】 如图,已知某几何体的三视图如图(单位:cm).
(1)画出这个几何体的直观图(不要求写画法);解:(1)这个几何体的直观图如图所示.(2)求这个几何体的表面积及体积.方法技巧 求组合体表面积与体积时应注意的问题
(1)首先应弄清它的组成,其表面有哪些底面和侧面,各个面应怎样求其面积,然后把这些面的面积相加或相减;求体积时也要先弄清组成,求出各简单几何体的体积,然后再相加或相减.
(2)在求组合体的表面积、体积时要注意“表面(和外界直接接触的面)”与“体积(几何体所占空间的大小)”的定义,以确保不重复、不遗漏.即时训练3-1:一个几何体的三视图如图所示(单位:m),则该几何体的体积为 m3.?3-2:已知正方体ABCD-A1B1C1D1,E,F是BD上的动点,P是AD1上的动点,则( )(1) (2) (3)
1.3.1 柱体、锥体、台体的表面积与体积课标要求:1.通过对柱、锥、台体的研究,掌握柱、锥、台体的表面积的求法.2.了解柱、锥、台体的表面积计算公式;能运用柱、锥、台的表面积公式进行计算和解决有关实际问题.3.培养空间想象能力和思维能力.自主学习知识探究1.柱体、锥体、台体的表面积
(1)棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台是由多个平面图形围成的多面体,它们的表面积就是各个面的 和.
(2)圆柱、圆锥、圆台的表面积公式面积底面半径侧面母线长底面半径侧面母线长上底面半径下底面半径侧面母线长2.柱体、锥体与台体的体积公式底面积 高 底面积 高 上、下底面面积 高 自我检测(教师备用)1.已知圆锥的母线长为5,底面周长为6π,则它的体积为( )
(A)36π (B)30π
(C)24π (D)12πD 2.若圆台的高为4,母线长为5,侧面积为45π,则圆台的上、下底面的面积之和为( )
(A)9π (B)36π
(C)45π (D)81πC 3.已知一个几何体的三视图如图所示,则该几何体的体积为( )
(A)12π (B)8π
(C) (D)D 4.某四棱锥的三视图如图所示,则该四棱锥的表面积是( )B (A)32 (B)16+16
(C)48 (D)16+325.已知圆锥的全面积是底面积的3倍,那么该圆锥的侧面展开扇形的圆心角为 .?答案:180°题型一 空间几何体的表面积【例1-1】 将圆心角为120°,面积为3π的扇形作为圆锥的侧面,则圆锥的表面积为 .?课堂探究答案:4π【1-2】 一个四面体的三视图如图所示,则该四面体的表面积是( )方法技巧 (1)多面体的表面积转化为各面面积之和.
(2)解决有关棱台的问题时,常用两种解题思路:一是把基本量转化到直角梯形中去解决;二是把棱台还原成棱锥,利用棱锥的有关知识来解决.
(3)旋转体中,求面积应注意侧面展开图,上下面圆的周长是展开图的弧长.圆台通常还要还原为圆锥.即时训练1-1:(1)圆柱的底面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是( )
(A)4πS (B)2πS (C)πS (D) πS(2)一个几何体的三视图及尺寸如图所示,其中正视图、侧视图都是等腰三角形,俯视图是圆,则该几何体的表面积是( )
(A)12π (B)14π
(C)16π (D)28π题型二 空间几何体的体积【例2-1】 (12分)圆锥的轴截面是等腰直角三角形,侧面积是16 π,求圆锥的体积.【2-2】 如图,圆台高为3,轴截面中母线AA1与底面直径AB的夹角为60°,轴截面中一条对角线垂直于腰,求圆台的体积.方法技巧 (1)常见的求几何体体积的方法
①公式法:直接代入公式求解.
②等积法:如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可.
③分割法:将几何体分割成易求解的几部分,分别求体积.
(2)求几何体体积时需注意的问题
柱、锥、台的体积的计算,一般要找出相应的底面和高,要充分利用截面、轴截面,求出所需要的量,最后代入公式计算.即时训练2-1:一个几何体的三视图如图所示,则该几何体的体积为( )(A) (B)π
(C) (D)2π2-2:(1)在棱长为1的正方体上,分别用过共顶点的三条棱的中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是 .?(2)如图所示,梯形ABCD中,AD∥BC,∠ABC=90°,AD=a, BC=2a,∠DCB= 60°,在平面ABCD内过点C作l⊥CB,以l为轴旋转一周.求旋转体的表面积和体积.题型三组合体的表面积与体积【例3】 如图,已知某几何体的三视图如图(单位:cm).
(1)画出这个几何体的直观图(不要求写画法);解:(1)这个几何体的直观图如图所示.(2)求这个几何体的表面积及体积.方法技巧 求组合体表面积与体积时应注意的问题
(1)首先应弄清它的组成,其表面有哪些底面和侧面,各个面应怎样求其面积,然后把这些面的面积相加或相减;求体积时也要先弄清组成,求出各简单几何体的体积,然后再相加或相减.
(2)在求组合体的表面积、体积时要注意“表面(和外界直接接触的面)”与“体积(几何体所占空间的大小)”的定义,以确保不重复、不遗漏.即时训练3-1:一个几何体的三视图如图所示(单位:m),则该几何体的体积为 m3.?3-2:已知正方体ABCD-A1B1C1D1,E,F是BD上的动点,P是AD1上的动点,则( )(1) (2) (3)
