北师大版七年级数学下册培优练习附答案:5.1 轴对称现象
文档属性
| 名称 | 北师大版七年级数学下册培优练习附答案:5.1 轴对称现象 |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 12:24:11 | ||
图片预览

文档简介
5.1 轴对称现象
一、选择题(共15小题)
1. 下面有 个汽车标志图案,其中不是轴对称图形的是
A. B.
C. D.
2. 如图, 与 关于直线 成轴对称,则下列结论中错误的是
A. B.
C. D. 直线 垂直平分线段
3. 下列图案是轴对称图形的有 个.
A. B. C. D.
4. 如图所示,在 正方形网格中,已有三个小正方形被涂黑,将剩余的白色小正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有
A. 种 B. 种 C. 种 D. 种
5. 如图 ①是 正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形 的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有
A. 种 B. 种 C. 种 D. 种
6. 如图,将一条两边沿互相平行的纸带按图折叠,则 的度数等于
A. B. C. D.
7. 小强将一张正方形纸片按如图所示对折两次,并在如图位置上剪去一个小正方形,然后把纸片
展开,得到的图形应是
A. B.
C. D.
8. 如图,把长方形 沿 折叠后使两部分重合,若 ,则 等于
A. B. C. D.
9. 已知正六边形 ,下列图形中不是轴对称图形的是
A. B.
C. D.
10. 如图,在 中,,, 是 上一点,将 沿 折叠,使 点落在 边上的 处,则 等于
A. B. C. D.
11. 下列图形中的五边形 都是正五边形,则这些图形中的轴对称图形有
A. 个 B. 个 C. 个 D. 个
12. 如图, 的周长为 ,把其边 对折,使点 , 重合,折痕交 边于点 ,交 边于点 ,连接 ,若 ,则 的周长是
A. B. C. D.
13. 如图所示, 是 外的一点,, 分别是 两边上的点,点 关于 的对称点 恰好落在线段 上,点 关于 的对称点 落在 的延长线上.若 ,,,则线段 的长为
A. B. C. D.
14. 如图a是长方形纸带,,将纸带沿 折叠成图b,再沿 折叠成图 c,则图 c 中的 的度数是
A. B. C. D.
15. 如图, 内有一点 , 点关于 的轴对称点是 , 点关于 的轴对称点是 , 分别交 , 于 , 点.若 的长为 ,求 的周长为
A. B. C. D.
二、填空题(共8小题)
16. 在线段、角、圆、等腰三角形、平行四边形、正方形中不是轴对称图形的是 ?.
17. 如图,将 的 沿 折叠使 与 重合.若 的周长为 ,,则 的长是 ?.
18. 如图,将一个长方形纸条折成如图的形状,若已知 ,则 ? .
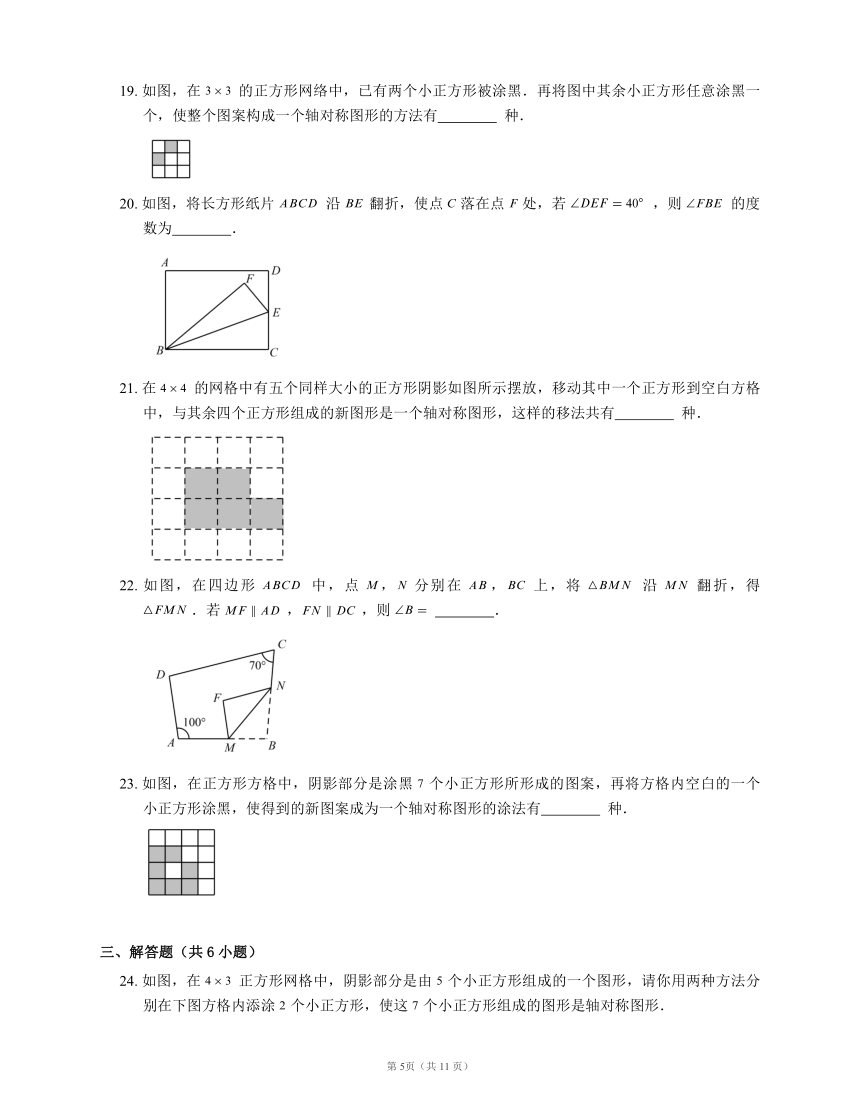
19. 如图,在 的正方形网络中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有 ? 种.
20. 如图,将长方形纸片 沿 翻折,使点 落在点 处,若 ,则 的度数为 ?.
21. 在 的网格中有五个同样大小的正方形阴影如图所示摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有 ? 种.
22. 如图,在四边形 中,点 , 分别在 , 上,将 沿 翻折,得 .若 ,,则 ?.
23. 如图,在正方形方格中,阴影部分是涂黑 个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有 ? 种.
三、解答题(共6小题)
24. 如图,在 正方形网格中,阴影部分是由 个小正方形组成的一个图形,请你用两种方法分别在下图方格内添涂 个小正方形,使这 个小正方形组成的图形是轴对称图形.
25. 如图: 的周长为 ,把 的边 对折,使顶点 和点 重合,折痕交 边于点 ,交 边于点 ,连接 ,若 ,求 的周长.
26. 如图,三角形纸片中,,,.沿过点 的直线折叠这个三角形,使点 落在 边上的点 处,折痕为 ,求 的周长.
27. 某住宅小区拟栽种 棵风景树,想栽成 行,每行 棵,且 行树所处位置连成线后能组成精美的轴对称(如图①所示),请你仿照举例在如图②③方框中再设计两种不同的栽树方案.
28. 如图,, 为 上一点, 点和 点关于 对称, 点、 点关于 对称,求 和 的度数.
29. 在 的正方形网格中,有格点三角形 和三角形 ,且 和 关于某直线成轴对称,请在下面的图中画出所有这样的 .
答案
1. D
2. C 【解析】 与 关于直线 成轴对称,
,,直线 垂直平分 .
3. B
4. C
5. C
6. C
7. B
8. A
9. D
10. C
11. D
12. A 【解析】 的边 对折后顶点 和顶点 重合,
,,
,
.
的周长为 ,
,
.
故 的周长为 .
13. A 【解析】由题意得 ,,
故 .
14. B
15. B
16. 平行四边形
【解析】线段是轴对称图形;角是轴对称图形;等腰三角形是轴对称图形;平行四边形不是轴对称图形;正方形是轴对称图形.
17.
18.
19.
20.
21.
【解析】
有 种;
有 种;
有 种;
有 种;
有 种.
22.
【解析】提示:, ,
, .
23.
【解析】在 ,, 处涂黑都可得到一个轴对称图形.
24. 如图所示,(答案不唯一).
25. 由图形和题意可知:,,
则 ,
故 的周长 ,
即可求出周长为 .
26. 沿 折叠后点 落在 边上的点 处,
,,
,,
,
27. 利用两个上下倒置的等边三角形进行设计,每个交点处种一棵树即可.
答案不唯一,如答图所示.
28. 根据题意 点和 点关于 对称,
有 ,即 .
点、 点关于 对称,
有 ,.
因为 ,
因为 ,
所以 ,.
29. 如图所示.
一、选择题(共15小题)
1. 下面有 个汽车标志图案,其中不是轴对称图形的是
A. B.
C. D.
2. 如图, 与 关于直线 成轴对称,则下列结论中错误的是
A. B.
C. D. 直线 垂直平分线段
3. 下列图案是轴对称图形的有 个.
A. B. C. D.
4. 如图所示,在 正方形网格中,已有三个小正方形被涂黑,将剩余的白色小正方形再任意涂黑一个,则所得黑色图案是轴对称图形的情况有
A. 种 B. 种 C. 种 D. 种
5. 如图 ①是 正方形方格,将其中两个方格涂黑,并且使涂黑后的整个图案是轴对称图形,约定绕正方形 的中心旋转能重合的图案都视为同一种图案,例如图②中的四幅图就视为同一种图案,则得到的不同图案共有
A. 种 B. 种 C. 种 D. 种
6. 如图,将一条两边沿互相平行的纸带按图折叠,则 的度数等于
A. B. C. D.
7. 小强将一张正方形纸片按如图所示对折两次,并在如图位置上剪去一个小正方形,然后把纸片
展开,得到的图形应是
A. B.
C. D.
8. 如图,把长方形 沿 折叠后使两部分重合,若 ,则 等于
A. B. C. D.
9. 已知正六边形 ,下列图形中不是轴对称图形的是
A. B.
C. D.
10. 如图,在 中,,, 是 上一点,将 沿 折叠,使 点落在 边上的 处,则 等于
A. B. C. D.
11. 下列图形中的五边形 都是正五边形,则这些图形中的轴对称图形有
A. 个 B. 个 C. 个 D. 个
12. 如图, 的周长为 ,把其边 对折,使点 , 重合,折痕交 边于点 ,交 边于点 ,连接 ,若 ,则 的周长是
A. B. C. D.
13. 如图所示, 是 外的一点,, 分别是 两边上的点,点 关于 的对称点 恰好落在线段 上,点 关于 的对称点 落在 的延长线上.若 ,,,则线段 的长为
A. B. C. D.
14. 如图a是长方形纸带,,将纸带沿 折叠成图b,再沿 折叠成图 c,则图 c 中的 的度数是
A. B. C. D.
15. 如图, 内有一点 , 点关于 的轴对称点是 , 点关于 的轴对称点是 , 分别交 , 于 , 点.若 的长为 ,求 的周长为
A. B. C. D.
二、填空题(共8小题)
16. 在线段、角、圆、等腰三角形、平行四边形、正方形中不是轴对称图形的是 ?.
17. 如图,将 的 沿 折叠使 与 重合.若 的周长为 ,,则 的长是 ?.
18. 如图,将一个长方形纸条折成如图的形状,若已知 ,则 ? .
19. 如图,在 的正方形网络中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有 ? 种.
20. 如图,将长方形纸片 沿 翻折,使点 落在点 处,若 ,则 的度数为 ?.
21. 在 的网格中有五个同样大小的正方形阴影如图所示摆放,移动其中一个正方形到空白方格中,与其余四个正方形组成的新图形是一个轴对称图形,这样的移法共有 ? 种.
22. 如图,在四边形 中,点 , 分别在 , 上,将 沿 翻折,得 .若 ,,则 ?.
23. 如图,在正方形方格中,阴影部分是涂黑 个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有 ? 种.
三、解答题(共6小题)
24. 如图,在 正方形网格中,阴影部分是由 个小正方形组成的一个图形,请你用两种方法分别在下图方格内添涂 个小正方形,使这 个小正方形组成的图形是轴对称图形.
25. 如图: 的周长为 ,把 的边 对折,使顶点 和点 重合,折痕交 边于点 ,交 边于点 ,连接 ,若 ,求 的周长.
26. 如图,三角形纸片中,,,.沿过点 的直线折叠这个三角形,使点 落在 边上的点 处,折痕为 ,求 的周长.
27. 某住宅小区拟栽种 棵风景树,想栽成 行,每行 棵,且 行树所处位置连成线后能组成精美的轴对称(如图①所示),请你仿照举例在如图②③方框中再设计两种不同的栽树方案.
28. 如图,, 为 上一点, 点和 点关于 对称, 点、 点关于 对称,求 和 的度数.
29. 在 的正方形网格中,有格点三角形 和三角形 ,且 和 关于某直线成轴对称,请在下面的图中画出所有这样的 .
答案
1. D
2. C 【解析】 与 关于直线 成轴对称,
,,直线 垂直平分 .
3. B
4. C
5. C
6. C
7. B
8. A
9. D
10. C
11. D
12. A 【解析】 的边 对折后顶点 和顶点 重合,
,,
,
.
的周长为 ,
,
.
故 的周长为 .
13. A 【解析】由题意得 ,,
故 .
14. B
15. B
16. 平行四边形
【解析】线段是轴对称图形;角是轴对称图形;等腰三角形是轴对称图形;平行四边形不是轴对称图形;正方形是轴对称图形.
17.
18.
19.
20.
21.
【解析】
有 种;
有 种;
有 种;
有 种;
有 种.
22.
【解析】提示:, ,
, .
23.
【解析】在 ,, 处涂黑都可得到一个轴对称图形.
24. 如图所示,(答案不唯一).
25. 由图形和题意可知:,,
则 ,
故 的周长 ,
即可求出周长为 .
26. 沿 折叠后点 落在 边上的点 处,
,,
,,
,
27. 利用两个上下倒置的等边三角形进行设计,每个交点处种一棵树即可.
答案不唯一,如答图所示.
28. 根据题意 点和 点关于 对称,
有 ,即 .
点、 点关于 对称,
有 ,.
因为 ,
因为 ,
所以 ,.
29. 如图所示.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
