北师大版七年级数学下册培优练习附答案:5.2 探索轴对称的性质
文档属性
| 名称 | 北师大版七年级数学下册培优练习附答案:5.2 探索轴对称的性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 00:00:00 | ||
图片预览


文档简介
5.2 探索轴对称的性质
一、选择题(共15小题)
1. 如图是把一张长方形的纸沿长边中点的连线对折两次后得到的图形,再沿虚线裁剪,外面部分展开后的图形是
A. B.
C. D.
2. 如图,将一个三角形纸片 沿过点 的直线折叠,使点 落在 边上的点 处,折痕为 ,则下列结论一定正确的是
A. B. C. D.
3. 下图中序号()()()()对应的四个三角形,都是 这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是
A. () B. () C. () D. ()
4. 下列说法正确的是
A. 如果图形甲和图形乙关于直线 对称,则图形甲是轴对称图形
B. 任何一个图形都有对称轴,有的图形不止一条对称轴
C. 平面上两个大小、形状完全一样的图形一定关于某直线对称
D. 如果 和 成轴对称,那么它们的面积一定相等
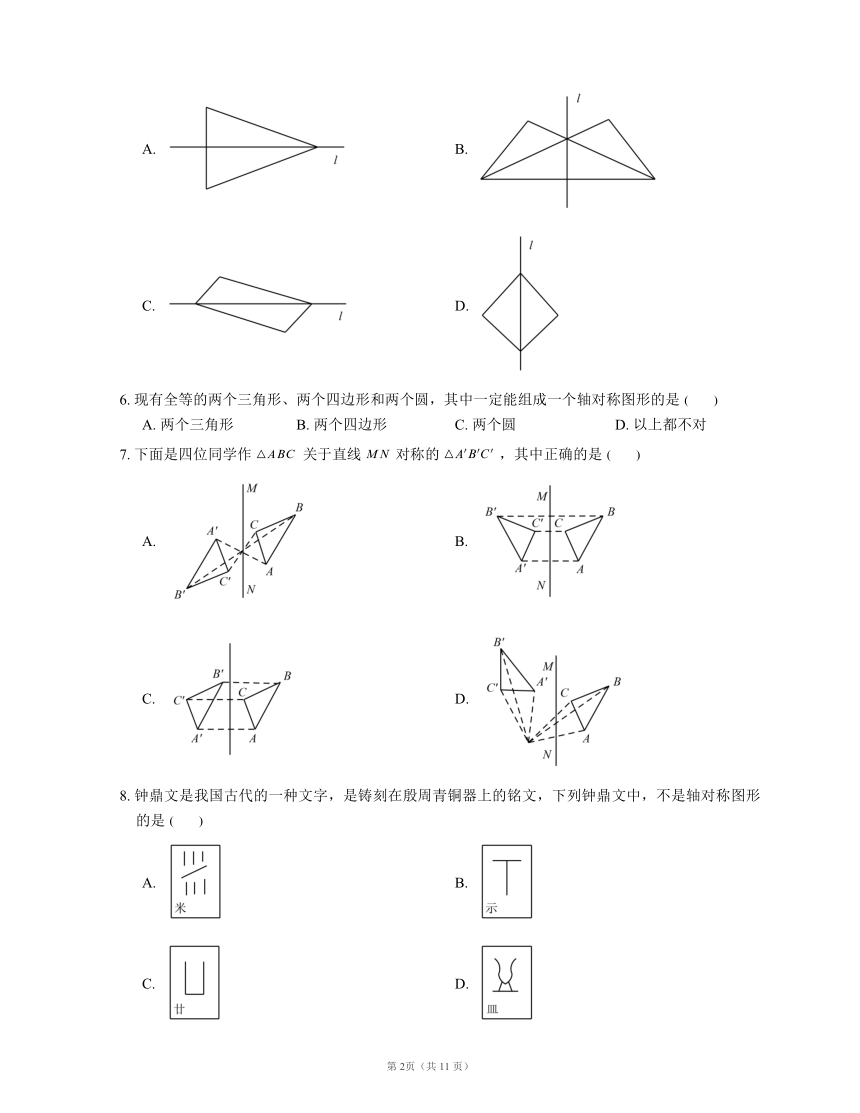
5. 分别以直线 为对称轴,所作轴对称图形错误的是
A. B.
C. D.
6. 现有全等的两个三角形、两个四边形和两个圆,其中一定能组成一个轴对称图形的是
A. 两个三角形 B. 两个四边形 C. 两个圆 D. 以上都不对
7. 下面是四位同学作 关于直线 对称的 ,其中正确的是
A. B.
C. D.
8. 钟鼎文是我国古代的一种文字,是铸刻在殷周青铜器上的铭文,下列钟鼎文中,不是轴对称图形的是
A. B.
C. D.
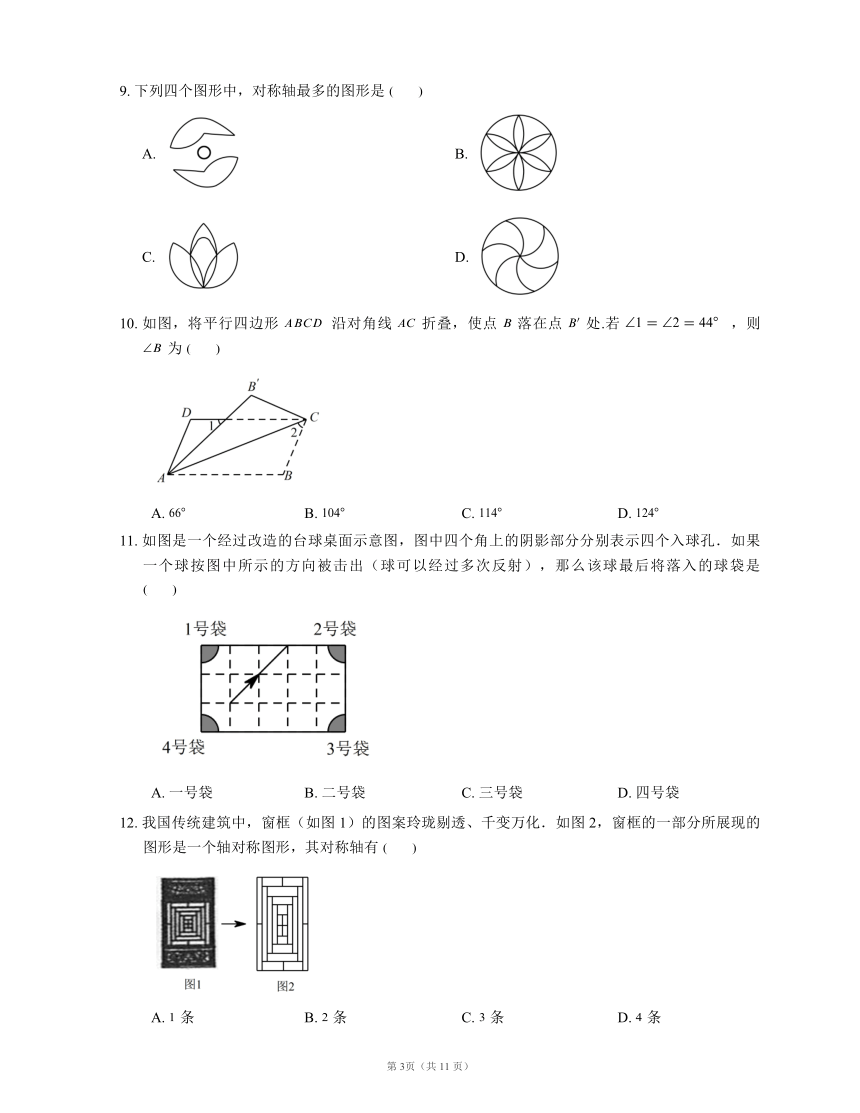
9. 下列四个图形中,对称轴最多的图形是
A. B.
C. D.
10. 如图,将平行四边形 沿对角线 折叠,使点 落在点 处.若 ,则 为
A. B. C. D.
11. 如图是一个经过改造的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是
A. 一号袋 B. 二号袋 C. 三号袋 D. 四号袋
12. 我国传统建筑中,窗框(如图1)的图案玲珑剔透、千变万化.如图2,窗框的一部分所展现的图形是一个轴对称图形,其对称轴有
A. 条 B. 条 C. 条 D. 条
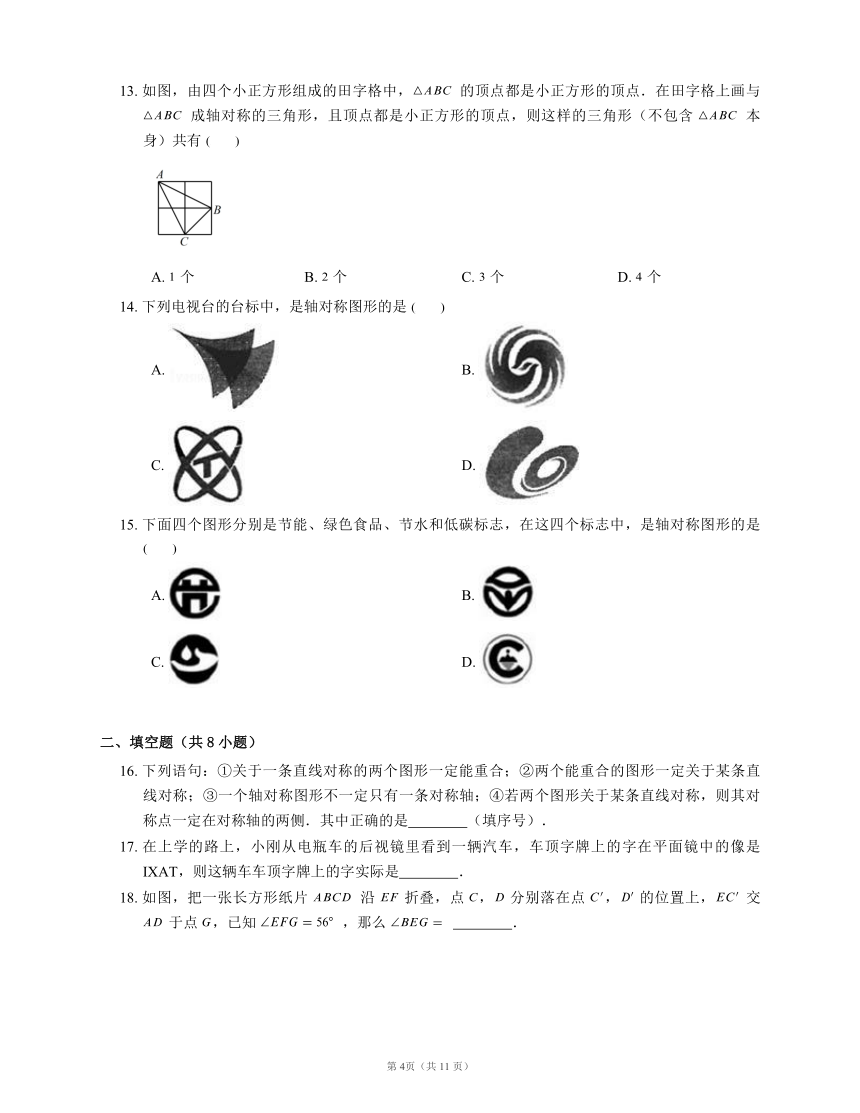
13. 如图,由四个小正方形组成的田字格中, 的顶点都是小正方形的顶点.在田字格上画与 成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含 本身)共有
A. 个 B. 个 C. 个 D. 个
14. 下列电视台的台标中,是轴对称图形的是
A. B.
C. D.
15. 下面四个图形分别是节能、绿色食品、节水和低碳标志,在这四个标志中,是轴对称图形的是
A. B.
C. D.
二、填空题(共8小题)
16. 下列语句:①关于一条直线对称的两个图形一定能重合;②两个能重合的图形一定关于某条直线对称;③一个轴对称图形不一定只有一条对称轴;④若两个图形关于某条直线对称,则其对称点一定在对称轴的两侧.其中正确的是 ?(填序号).
17. 在上学的路上,小刚从电瓶车的后视镜里看到一辆汽车,车顶字牌上的字在平面镜中的像是 IXAT,则这辆车车顶字牌上的字实际是 ?.
18. 如图,把一张长方形纸片 沿 折叠,点 , 分别落在点 , 的位置上, 交 于点 ,已知 ,那么 ?.
19. 如图,在由四个小正方形组成的田字格中, 的顶点都是小正方形的顶点.在田字格上画与 成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形共有 ? 个.
20. 如图,在 的正方形网格中,已有 个小方格涂成了灰色,现在要从其余白色小方格中选出一个也涂成灰色,使整个灰色部分的图形构成轴对称图形,这样的白色小方格有 ? 个.
21. 如图,将一张纸条折叠,若 ,则 的度数为 ?.
22. 如图,将 放在每个小正方形的边长为 的网格中,点 ,点 ,点 均落在格点上.
(I) 的面积等于 ?;
(II)请在如图所示的网格中,用无刻度的直尺,以 所在直线为对称轴,作出 关于直线 对称的图形,并简要说明画图方法(不要求证明) ?.
23. 如图,,, 与 关于直线 对称,则 ?.
三、解答题(共6小题)
24. 画出 关于直线 的对称图形.
25. 我们已学习了角平分线的概念,那么你会用他们解决有关问题吗?
(1)如图 所示,将长方形笔记本活页纸片的一角折过去,使角的顶点 落在 处, 为折痕.若 ,求 的度数.
(2)在()条件下,如果又将它的另一个角也斜折过去,并使 边与 重合,折痕为 ,如图 所示,求 和 的度数.
(3)如果在图 中改变 的大小,则 的位置也随之改变,那么()中 的大小会不会改变?请说明.
26. (1)图(8)是边长为 的小正方形组成的网格,观察① ④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征:
?;
?;
(2)借助图中⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与图① ④的图案不能重合).
27. 如图所示, 与 关于直线 对称, 与 的交点 在直线 上.
(1)指出此两个三角形中三个顶点的对称点.
(2)在不另加字母和线段的情况下,图中还有成轴对称的三角形吗?
28. 把图中的图形补成轴对称图形,其中 , 为各图形的对称轴.
29. 资料:小球沿直线撞击水平格档反弹时(不考虑垂直撞击),撞击路线与水平格档所成的锐角等于反弹路线与水平格档所成的锐角.以图(1)为例,如果黑球 沿从 到 方向在 点处撞击 边后将沿从 到 方向反弹,根据反弹原则可知 ,即 .如图(2)和(3), 是一个长方形的弹子球台面,有黑白两球 和 ,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)
(1)探究(1):黑球 沿直线撞击台边 哪一点时,可以使黑球 经台边 反弹一次后撞击到白球 ?请在图(2)中画出黑球 的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则,
(2)探究(2):黑球 沿直线撞击台边 哪一点时,可以使黑球 先撞击台边 反弹一次后,再撞击台边 反弹一次撞击到白球 ?请在图(3)中画出黑球 的路线图,标出黑球撞击 边的撞击点,简单说明作法,不用证明.
答案
1. D
2. D
3. A
4. D
5. C
6. C
7. B
8. A
9. B
10. C
【解析】因为 ,,由于折叠,,在 中,.
11. B
12. B
13. C
14. A
15. B
16. ①③
17. TAXI
18.
19.
20.
21.
22. ,如图,
取格点 ,,连接 .取格点 ,作直线 与 相交,得点 .连接 ,.则 即为所求
23.
【解析】 与 关于直线 对称,
,
,
,
.
24. 如图所示, 即为所求.
25. (1) ,
,
;
??????(2) 由()的结论可得 ,
由折叠的性质可得,
,
;
??????(3) 不变,由折叠的性质可得,
,,
所以 ,
不变,永远是平角的一半.
26. (1) 都是轴对称图形;面积都是
??????(2)
(答案不唯一)
27. (1) 点 的对称点是点 ,点 的对称点是点 ,点 的对称点是点 .
??????(2) 在不另加字母和线段的情况下, 与 , 与 也都关于直线 成轴对称.
28. 如图所示:
29. (1) 作法:如图以直线 为对称轴作点 的对称点 ,连接 交 于点 ,连接 ,
则点 为撞击点, 和 为黑球 的路线.
证明:
因为 和 关于直线 对称,点 在 上,
所以 和 也关于 对称,
因为 和 是对应角,
所以 ,
又 (对顶角相等),
所以 ,即符合反弹原则,
??????(2) 以直线 为对称轴作点 的对称点 ,再以 为对称轴作点 的对称点 ,连接 交 于点 ,连接 交 于点 ,连接 .
则点 为 边的撞击点,,, 为球 的路线.
一、选择题(共15小题)
1. 如图是把一张长方形的纸沿长边中点的连线对折两次后得到的图形,再沿虚线裁剪,外面部分展开后的图形是
A. B.
C. D.
2. 如图,将一个三角形纸片 沿过点 的直线折叠,使点 落在 边上的点 处,折痕为 ,则下列结论一定正确的是
A. B. C. D.
3. 下图中序号()()()()对应的四个三角形,都是 这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是
A. () B. () C. () D. ()
4. 下列说法正确的是
A. 如果图形甲和图形乙关于直线 对称,则图形甲是轴对称图形
B. 任何一个图形都有对称轴,有的图形不止一条对称轴
C. 平面上两个大小、形状完全一样的图形一定关于某直线对称
D. 如果 和 成轴对称,那么它们的面积一定相等
5. 分别以直线 为对称轴,所作轴对称图形错误的是
A. B.
C. D.
6. 现有全等的两个三角形、两个四边形和两个圆,其中一定能组成一个轴对称图形的是
A. 两个三角形 B. 两个四边形 C. 两个圆 D. 以上都不对
7. 下面是四位同学作 关于直线 对称的 ,其中正确的是
A. B.
C. D.
8. 钟鼎文是我国古代的一种文字,是铸刻在殷周青铜器上的铭文,下列钟鼎文中,不是轴对称图形的是
A. B.
C. D.
9. 下列四个图形中,对称轴最多的图形是
A. B.
C. D.
10. 如图,将平行四边形 沿对角线 折叠,使点 落在点 处.若 ,则 为
A. B. C. D.
11. 如图是一个经过改造的台球桌面示意图,图中四个角上的阴影部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入的球袋是
A. 一号袋 B. 二号袋 C. 三号袋 D. 四号袋
12. 我国传统建筑中,窗框(如图1)的图案玲珑剔透、千变万化.如图2,窗框的一部分所展现的图形是一个轴对称图形,其对称轴有
A. 条 B. 条 C. 条 D. 条
13. 如图,由四个小正方形组成的田字格中, 的顶点都是小正方形的顶点.在田字格上画与 成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含 本身)共有
A. 个 B. 个 C. 个 D. 个
14. 下列电视台的台标中,是轴对称图形的是
A. B.
C. D.
15. 下面四个图形分别是节能、绿色食品、节水和低碳标志,在这四个标志中,是轴对称图形的是
A. B.
C. D.
二、填空题(共8小题)
16. 下列语句:①关于一条直线对称的两个图形一定能重合;②两个能重合的图形一定关于某条直线对称;③一个轴对称图形不一定只有一条对称轴;④若两个图形关于某条直线对称,则其对称点一定在对称轴的两侧.其中正确的是 ?(填序号).
17. 在上学的路上,小刚从电瓶车的后视镜里看到一辆汽车,车顶字牌上的字在平面镜中的像是 IXAT,则这辆车车顶字牌上的字实际是 ?.
18. 如图,把一张长方形纸片 沿 折叠,点 , 分别落在点 , 的位置上, 交 于点 ,已知 ,那么 ?.
19. 如图,在由四个小正方形组成的田字格中, 的顶点都是小正方形的顶点.在田字格上画与 成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形共有 ? 个.
20. 如图,在 的正方形网格中,已有 个小方格涂成了灰色,现在要从其余白色小方格中选出一个也涂成灰色,使整个灰色部分的图形构成轴对称图形,这样的白色小方格有 ? 个.
21. 如图,将一张纸条折叠,若 ,则 的度数为 ?.
22. 如图,将 放在每个小正方形的边长为 的网格中,点 ,点 ,点 均落在格点上.
(I) 的面积等于 ?;
(II)请在如图所示的网格中,用无刻度的直尺,以 所在直线为对称轴,作出 关于直线 对称的图形,并简要说明画图方法(不要求证明) ?.
23. 如图,,, 与 关于直线 对称,则 ?.
三、解答题(共6小题)
24. 画出 关于直线 的对称图形.
25. 我们已学习了角平分线的概念,那么你会用他们解决有关问题吗?
(1)如图 所示,将长方形笔记本活页纸片的一角折过去,使角的顶点 落在 处, 为折痕.若 ,求 的度数.
(2)在()条件下,如果又将它的另一个角也斜折过去,并使 边与 重合,折痕为 ,如图 所示,求 和 的度数.
(3)如果在图 中改变 的大小,则 的位置也随之改变,那么()中 的大小会不会改变?请说明.
26. (1)图(8)是边长为 的小正方形组成的网格,观察① ④中阴影部分构成的图案,请写出这四个图案都具有的两个共同特征:
?;
?;
(2)借助图中⑤的网格,请设计一个新的图案,使该图案同时具有你在解答(1)中所写出的两个共同特征.(注意:新图案与图① ④的图案不能重合).
27. 如图所示, 与 关于直线 对称, 与 的交点 在直线 上.
(1)指出此两个三角形中三个顶点的对称点.
(2)在不另加字母和线段的情况下,图中还有成轴对称的三角形吗?
28. 把图中的图形补成轴对称图形,其中 , 为各图形的对称轴.
29. 资料:小球沿直线撞击水平格档反弹时(不考虑垂直撞击),撞击路线与水平格档所成的锐角等于反弹路线与水平格档所成的锐角.以图(1)为例,如果黑球 沿从 到 方向在 点处撞击 边后将沿从 到 方向反弹,根据反弹原则可知 ,即 .如图(2)和(3), 是一个长方形的弹子球台面,有黑白两球 和 ,小球沿直线撞击各边反弹时遵循资料中的反弹原则.(回答以下问题时将黑白两球均看作几何图形中的点,不考虑其半径大小)
(1)探究(1):黑球 沿直线撞击台边 哪一点时,可以使黑球 经台边 反弹一次后撞击到白球 ?请在图(2)中画出黑球 的路线图,标出撞击点,并简单证明所作路线是否符合反弹原则,
(2)探究(2):黑球 沿直线撞击台边 哪一点时,可以使黑球 先撞击台边 反弹一次后,再撞击台边 反弹一次撞击到白球 ?请在图(3)中画出黑球 的路线图,标出黑球撞击 边的撞击点,简单说明作法,不用证明.
答案
1. D
2. D
3. A
4. D
5. C
6. C
7. B
8. A
9. B
10. C
【解析】因为 ,,由于折叠,,在 中,.
11. B
12. B
13. C
14. A
15. B
16. ①③
17. TAXI
18.
19.
20.
21.
22. ,如图,
取格点 ,,连接 .取格点 ,作直线 与 相交,得点 .连接 ,.则 即为所求
23.
【解析】 与 关于直线 对称,
,
,
,
.
24. 如图所示, 即为所求.
25. (1) ,
,
;
??????(2) 由()的结论可得 ,
由折叠的性质可得,
,
;
??????(3) 不变,由折叠的性质可得,
,,
所以 ,
不变,永远是平角的一半.
26. (1) 都是轴对称图形;面积都是
??????(2)
(答案不唯一)
27. (1) 点 的对称点是点 ,点 的对称点是点 ,点 的对称点是点 .
??????(2) 在不另加字母和线段的情况下, 与 , 与 也都关于直线 成轴对称.
28. 如图所示:
29. (1) 作法:如图以直线 为对称轴作点 的对称点 ,连接 交 于点 ,连接 ,
则点 为撞击点, 和 为黑球 的路线.
证明:
因为 和 关于直线 对称,点 在 上,
所以 和 也关于 对称,
因为 和 是对应角,
所以 ,
又 (对顶角相等),
所以 ,即符合反弹原则,
??????(2) 以直线 为对称轴作点 的对称点 ,再以 为对称轴作点 的对称点 ,连接 交 于点 ,连接 交 于点 ,连接 .
则点 为 边的撞击点,,, 为球 的路线.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
