北师大版七年级数学下册培优练习:第三章变量之间的关系(含答案)
文档属性
| 名称 | 北师大版七年级数学下册培优练习:第三章变量之间的关系(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 18:21:59 | ||
图片预览




文档简介
第三章变量之间的关系
一、选择题(共15小题)
1. 面上有三点,经过每两点作一条直线,则能作出的直线的条数是
A. 条 B. 条 C. 条或 条 D. 以上都不对
2. 已知 是平面直角坐标系的点,则点 的纵坐标随横坐标变化的函数解析式可以是
A. B. C. D.
3. 下列图象分别给出了 与 的对应关系,其中 是 的函数的是
A. B.
C. D.
4. 已知两个变量 和 ,它们之间的 组对应值如下表:
则 与 之间的关系式可能是
A. B. C. D.
5. 在学雷锋活动中,某校团支部组织团员步行到敬老院去服务.他们从学校出发,走了一段时间后,发现团旗忘带了,于是派团员小明跑步返回学校去拿,小明沿原路返回学校拿了团旗后,立即又以原跑步速度追上了队伍.设小明与队伍之间的距离为 ,小明随队伍从学校出发到再次追上队伍的时间为 .下面能反映 与 的函数关系的大致图象是
A. B.
C. D.
6. 下列各图能表示 是 的函数是
A. B.
C. D.
7. 若 是完全平方式,则 的值为
A. B. 或 C. D. 或
8. 赵先生手中有一张记录他从出生到 岁期间的身高情况表(如下表所示):
对于赵先生从出生到 岁身高情况,下列说法错误的是
A. 赵先生的身高增长速度总体上先快后慢
B. 赵先生的身高在 岁以后基本不长了
C. 赵先生的身高从 岁到 岁平均每年约增高
D. 赵先生的身高从 岁到 岁平均每年增高
9. 中国电信公司最近推出的无线市话的收费标准如下:前 (不足 按 计)收费 元, 后每分钟 元.则通话一次的时间 与这次通话费用 (元)之间的关系是
A. B.
C. D.
10. 某学习小组做了一个试验:从一幢 高的楼的顶部随手扔下一个苹果,测得有关数据如下:
则下列说法错误的是
A. 苹果每秒下落的路程不变
B. 苹果每秒下落的路程越来越长
C. 苹果下落的速度越来越快
D. 可以推测出苹果落到地面的时间不超过
11. 如图所示,向一个半径为 、容积为 的球形容器内注水,则能够反映容器内水的体积 与容器内水深 之间的函数关系的图象的可能是
A. B.
C. D.
12. 如图,它表示甲乙两人从同一个地点出发后的情况.根据图象判断,下列说法错误的是
A. 甲是 点出发的
B. 乙是 点出发的,到 点时,他大约走了 千米
C. 到 点为止,乙的速度快
D. 两人在 点再次相遇
13. 已知线段 ,点 在直线 上,且线段 ,则线段 的长为
A. B. C. 或 D. 以上均不对
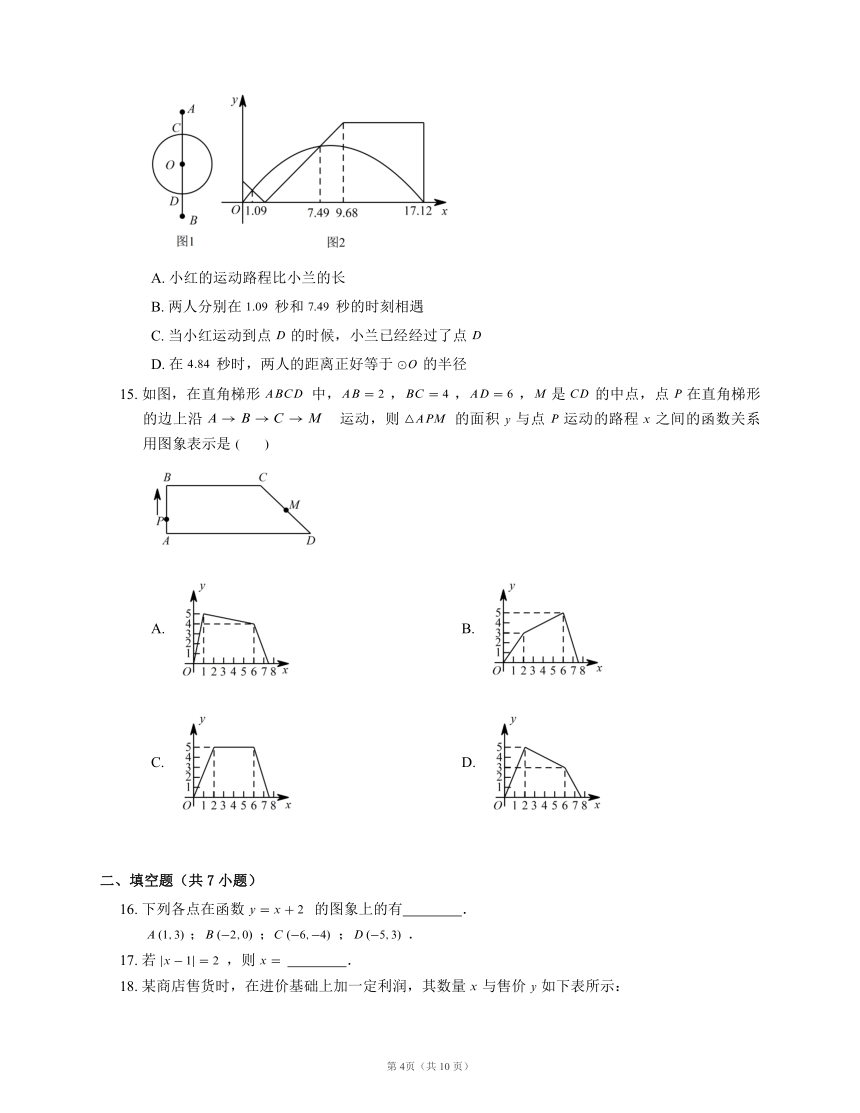
14. 两个少年在绿茵场上游戏.小红从点 出发沿线段 运动到点 ,小兰从点 出发,以相同的速度沿 逆时针运动一周回到点 ,两人的运动路线如图 所示,其中 .两人同时开始运动,直到都停止运动时游戏结束,其间他们与点 的距离 与时间 (单位:秒)的对应关系如图 所示.则下列说法正确的是
A. 小红的运动路程比小兰的长
B. 两人分别在 秒和 秒的时刻相遇
C. 当小红运动到点 的时候,小兰已经经过了点
D. 在 秒时,两人的距离正好等于 的半径
15. 如图,在直角梯形 中,,,, 是 的中点,点 在直角梯形的边上沿 运动,则 的面积 与点 运动的路程 之间的函数关系用图象表示是
A. B.
C. D.
二、填空题(共7小题)
16. 下列各点在函数 的图象上的有 ?.
;;;.
17. 若 ,则 ?.
18. 某商店售货时,在进价基础上加一定利润,其数量 与售价 如下表所示:
则售价 与数量 之间的函数关系式为 ?.
19. 下岗职工购进一批苹果,到集贸市场零售,已知卖出的苹果数量 (千克)与售价 (元)的关系如下表:
则 与 之间的关系式为 ?.
20. 已知函数 ,那么 ?.
21. 如图,是体检时的心电图,其中横坐标 表示时间,纵坐标 表示心脏部位的生物电流,它们是两个变量.在心电图中, ?(填“是”或“不是”) 的函数.
22. 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用 分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为 千米/时,两车之间的距离 (千米)与货车行驶时间 (小时)之间的函数图象如图所示,现有以下 个结论:
①快递车从甲地到乙地的速度为 千米/时;
②甲、乙两地之间的距离为 千米;
③图中点 的坐标为 ;
④快递车从乙地返回时的速度为 千米/时,以上 个结论正确的是 ?.
三、解答题(共6小题)
23. 在同一平面内,三条直线的交点有多少个?
甲:在同一平面内,三条直线的交点个数为 个,因为 , 如图①所示.
乙:在同一平面内,三条直线的交点个数只有 个,因为 ,,.交于同一点 , 如图②所示.
以上说法谁对谁错?为什么?
24. 小王周末骑电动车从家出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)小王从家到新华书店的路程是多少米?
(2)小王在新华书店停留了多少分钟?
(3)买到书后,小王从新华书店到商场的骑车速度是多少米 分钟?
25. 如果用 表示摄氏温度, 表示华氏温度,则 与 之间的关系为:,试分别求:
(1)当 和 时, 的值;
(2)当 时, 的值.
26. 已知 是 的函数,下表是 与 的几组对应值.
小明根据学习函数的经验,利用上述表格所反映出的 与 之间的变化规律,对该函数的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)如图,在平面直角坐标系 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
① 对应的函数值 约为 ?;
②该函数的一条性质: ?.
27. 如图,一个无上底面的四棱柱容器,底面是一个边长为 的正方形,其高为 ,现往容器内注水,水面高度 ,水的体积为 .
(1)在注水过程中, ?是自变量, ?是因变量;
(2)在注水过程中, 与 的关系为 ?;
(3)当水面高度由 变化到 ,水的体积增加多少?
28. 在一次实验中,马达同学把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度 与所挂物体质量 的一组对应值.
(1)上表反映了哪两个变量之间的关系, ?是自变量, ?是因变量.
(2)当所挂物体重量为 千克时,弹簧长 ?;不挂重物时弹簧长 ?.
(3)弹簧长度 与所挂物体质量 之间的关系可以用式子表示为: ?.
答案
1. C
2. B
3. B
4. B
5. C
6. D
7. D 【解析】,
,
解得 .
8. D 【解析】,
从 岁到 岁平均每年增高 是错误的.
9. C
10. A
11. A 【解析】容器内水深在 之间时,随着注水越深,水的截面越大,单位深度可容纳水的体积也越大,故曲线从缓慢增长到快速增长;容器内水深在 之间时,随着注水越深,水的截面越小,单位深度可容纳水的体积逐渐减小,故曲线从快速增长到缓慢增长.
12. B 【解析】从图象可知:甲做变速运动, 时到 时走了 千米,速度为每小时 千米, 时到 时走了 千米,速度为每小时 千米;乙做的是匀速运动, 时到 时走了 千米,速度是每小时 千米.
A.由图象知,甲 点出发,故A正确;
B.由图象知,乙 点出发;到 时他大约走了 千米,故B不正确;
C.到 时为止,甲的速度为每小时 千米,乙的速度是每小时 千米,乙的速度快,故C正确;
D.由图象知,两人最终在 时相遇,故D正确.
13. C 【解析】若点 在 , 之间则 的长度为 ;若点 线段 的延长线上,则 的长度为 .
14. D 【解析】由图 得,当 时,小红运动到点 .
小红是以相同的速度运动,
小红在 秒时,运动到点 ,小兰在 上运动,
两人距离为 的半径.
15. D
16. ,,
17. 或
【解析】由题意得,绝对值是 的数有 .
18.
19.
20.
21. 是
22. ①③④
23. 甲、乙说法都不对,都少了三种清况.
, 与 , 相交,如图①所示;,, 两两相交(不包括 ,, 交于一点的情况), 如图②所示.
所以在同一平面内,三条直线互不重合,交点个数为 个或 个或 个或 个,共四种情况.
24. (1) 根据函数图象,可知小王从家到新华书店的路程是 米.
??????(2) (分钟)
答:小王在书店停留了 分钟.
??????(3) (米 分钟)
答:买到书后,小王从新华书店到商场的骑车速度是 米 分钟.
25. (1) 当 时,,
当 时,;
??????(2) 当 时,,解得 .
26. (1) 如图:
??????(2) ① (答案不唯一);
②当 时, 随 的增大而减小;
当 时, 随 的增大而增大;
当 时, 有最小值为 .
(写出一条即可)
27. (1) 水面高度;水的体积
??????(2)
??????(3) 水面高度为 时,
.
水面高度为 时,
.
水体积增加为 .
28. (1) 上表反映了弹簧长度与所挂物体质量之间的关系;
所挂物体质量;弹簧长度
??????(2) ;
??????(3)
一、选择题(共15小题)
1. 面上有三点,经过每两点作一条直线,则能作出的直线的条数是
A. 条 B. 条 C. 条或 条 D. 以上都不对
2. 已知 是平面直角坐标系的点,则点 的纵坐标随横坐标变化的函数解析式可以是
A. B. C. D.
3. 下列图象分别给出了 与 的对应关系,其中 是 的函数的是
A. B.
C. D.
4. 已知两个变量 和 ,它们之间的 组对应值如下表:
则 与 之间的关系式可能是
A. B. C. D.
5. 在学雷锋活动中,某校团支部组织团员步行到敬老院去服务.他们从学校出发,走了一段时间后,发现团旗忘带了,于是派团员小明跑步返回学校去拿,小明沿原路返回学校拿了团旗后,立即又以原跑步速度追上了队伍.设小明与队伍之间的距离为 ,小明随队伍从学校出发到再次追上队伍的时间为 .下面能反映 与 的函数关系的大致图象是
A. B.
C. D.
6. 下列各图能表示 是 的函数是
A. B.
C. D.
7. 若 是完全平方式,则 的值为
A. B. 或 C. D. 或
8. 赵先生手中有一张记录他从出生到 岁期间的身高情况表(如下表所示):
对于赵先生从出生到 岁身高情况,下列说法错误的是
A. 赵先生的身高增长速度总体上先快后慢
B. 赵先生的身高在 岁以后基本不长了
C. 赵先生的身高从 岁到 岁平均每年约增高
D. 赵先生的身高从 岁到 岁平均每年增高
9. 中国电信公司最近推出的无线市话的收费标准如下:前 (不足 按 计)收费 元, 后每分钟 元.则通话一次的时间 与这次通话费用 (元)之间的关系是
A. B.
C. D.
10. 某学习小组做了一个试验:从一幢 高的楼的顶部随手扔下一个苹果,测得有关数据如下:
则下列说法错误的是
A. 苹果每秒下落的路程不变
B. 苹果每秒下落的路程越来越长
C. 苹果下落的速度越来越快
D. 可以推测出苹果落到地面的时间不超过
11. 如图所示,向一个半径为 、容积为 的球形容器内注水,则能够反映容器内水的体积 与容器内水深 之间的函数关系的图象的可能是
A. B.
C. D.
12. 如图,它表示甲乙两人从同一个地点出发后的情况.根据图象判断,下列说法错误的是
A. 甲是 点出发的
B. 乙是 点出发的,到 点时,他大约走了 千米
C. 到 点为止,乙的速度快
D. 两人在 点再次相遇
13. 已知线段 ,点 在直线 上,且线段 ,则线段 的长为
A. B. C. 或 D. 以上均不对
14. 两个少年在绿茵场上游戏.小红从点 出发沿线段 运动到点 ,小兰从点 出发,以相同的速度沿 逆时针运动一周回到点 ,两人的运动路线如图 所示,其中 .两人同时开始运动,直到都停止运动时游戏结束,其间他们与点 的距离 与时间 (单位:秒)的对应关系如图 所示.则下列说法正确的是
A. 小红的运动路程比小兰的长
B. 两人分别在 秒和 秒的时刻相遇
C. 当小红运动到点 的时候,小兰已经经过了点
D. 在 秒时,两人的距离正好等于 的半径
15. 如图,在直角梯形 中,,,, 是 的中点,点 在直角梯形的边上沿 运动,则 的面积 与点 运动的路程 之间的函数关系用图象表示是
A. B.
C. D.
二、填空题(共7小题)
16. 下列各点在函数 的图象上的有 ?.
;;;.
17. 若 ,则 ?.
18. 某商店售货时,在进价基础上加一定利润,其数量 与售价 如下表所示:
则售价 与数量 之间的函数关系式为 ?.
19. 下岗职工购进一批苹果,到集贸市场零售,已知卖出的苹果数量 (千克)与售价 (元)的关系如下表:
则 与 之间的关系式为 ?.
20. 已知函数 ,那么 ?.
21. 如图,是体检时的心电图,其中横坐标 表示时间,纵坐标 表示心脏部位的生物电流,它们是两个变量.在心电图中, ?(填“是”或“不是”) 的函数.
22. 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用 分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为 千米/时,两车之间的距离 (千米)与货车行驶时间 (小时)之间的函数图象如图所示,现有以下 个结论:
①快递车从甲地到乙地的速度为 千米/时;
②甲、乙两地之间的距离为 千米;
③图中点 的坐标为 ;
④快递车从乙地返回时的速度为 千米/时,以上 个结论正确的是 ?.
三、解答题(共6小题)
23. 在同一平面内,三条直线的交点有多少个?
甲:在同一平面内,三条直线的交点个数为 个,因为 , 如图①所示.
乙:在同一平面内,三条直线的交点个数只有 个,因为 ,,.交于同一点 , 如图②所示.
以上说法谁对谁错?为什么?
24. 小王周末骑电动车从家出发去商场买东西,当他骑了一段路时,想起要买一本书,于是原路返回到刚经过的新华书店,买到书后继续前往商场,如图是他离家的距离与时间的关系示意图,请根据图中提供的信息回答下列问题:
(1)小王从家到新华书店的路程是多少米?
(2)小王在新华书店停留了多少分钟?
(3)买到书后,小王从新华书店到商场的骑车速度是多少米 分钟?
25. 如果用 表示摄氏温度, 表示华氏温度,则 与 之间的关系为:,试分别求:
(1)当 和 时, 的值;
(2)当 时, 的值.
26. 已知 是 的函数,下表是 与 的几组对应值.
小明根据学习函数的经验,利用上述表格所反映出的 与 之间的变化规律,对该函数的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)如图,在平面直角坐标系 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
① 对应的函数值 约为 ?;
②该函数的一条性质: ?.
27. 如图,一个无上底面的四棱柱容器,底面是一个边长为 的正方形,其高为 ,现往容器内注水,水面高度 ,水的体积为 .
(1)在注水过程中, ?是自变量, ?是因变量;
(2)在注水过程中, 与 的关系为 ?;
(3)当水面高度由 变化到 ,水的体积增加多少?
28. 在一次实验中,马达同学把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度 与所挂物体质量 的一组对应值.
(1)上表反映了哪两个变量之间的关系, ?是自变量, ?是因变量.
(2)当所挂物体重量为 千克时,弹簧长 ?;不挂重物时弹簧长 ?.
(3)弹簧长度 与所挂物体质量 之间的关系可以用式子表示为: ?.
答案
1. C
2. B
3. B
4. B
5. C
6. D
7. D 【解析】,
,
解得 .
8. D 【解析】,
从 岁到 岁平均每年增高 是错误的.
9. C
10. A
11. A 【解析】容器内水深在 之间时,随着注水越深,水的截面越大,单位深度可容纳水的体积也越大,故曲线从缓慢增长到快速增长;容器内水深在 之间时,随着注水越深,水的截面越小,单位深度可容纳水的体积逐渐减小,故曲线从快速增长到缓慢增长.
12. B 【解析】从图象可知:甲做变速运动, 时到 时走了 千米,速度为每小时 千米, 时到 时走了 千米,速度为每小时 千米;乙做的是匀速运动, 时到 时走了 千米,速度是每小时 千米.
A.由图象知,甲 点出发,故A正确;
B.由图象知,乙 点出发;到 时他大约走了 千米,故B不正确;
C.到 时为止,甲的速度为每小时 千米,乙的速度是每小时 千米,乙的速度快,故C正确;
D.由图象知,两人最终在 时相遇,故D正确.
13. C 【解析】若点 在 , 之间则 的长度为 ;若点 线段 的延长线上,则 的长度为 .
14. D 【解析】由图 得,当 时,小红运动到点 .
小红是以相同的速度运动,
小红在 秒时,运动到点 ,小兰在 上运动,
两人距离为 的半径.
15. D
16. ,,
17. 或
【解析】由题意得,绝对值是 的数有 .
18.
19.
20.
21. 是
22. ①③④
23. 甲、乙说法都不对,都少了三种清况.
, 与 , 相交,如图①所示;,, 两两相交(不包括 ,, 交于一点的情况), 如图②所示.
所以在同一平面内,三条直线互不重合,交点个数为 个或 个或 个或 个,共四种情况.
24. (1) 根据函数图象,可知小王从家到新华书店的路程是 米.
??????(2) (分钟)
答:小王在书店停留了 分钟.
??????(3) (米 分钟)
答:买到书后,小王从新华书店到商场的骑车速度是 米 分钟.
25. (1) 当 时,,
当 时,;
??????(2) 当 时,,解得 .
26. (1) 如图:
??????(2) ① (答案不唯一);
②当 时, 随 的增大而减小;
当 时, 随 的增大而增大;
当 时, 有最小值为 .
(写出一条即可)
27. (1) 水面高度;水的体积
??????(2)
??????(3) 水面高度为 时,
.
水面高度为 时,
.
水体积增加为 .
28. (1) 上表反映了弹簧长度与所挂物体质量之间的关系;
所挂物体质量;弹簧长度
??????(2) ;
??????(3)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
