北师大版七年级数学下册培优练习3.3 用图象表示的变量间关系(附答案)
文档属性
| 名称 | 北师大版七年级数学下册培优练习3.3 用图象表示的变量间关系(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-23 00:00:00 | ||
图片预览



文档简介
3.3 用图象表示的变量间关系
一、选择题(共16小题)
1. 如果两个变量 , 之间的函数关系如图所示,则函数值 的取值范围是
A. B. C. D.
2. 数轴上到 的距离是 的点表示的数是
A. B. C. D. 或
3. 在 月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是
A. 月份 B. 月份 C. 月份 D. 月份
4. 小亮从家出发步行到公交站台后,等公交车去学校,如图,折线表示这个过程中行程 (千米)与所花时间 (分)之间的关系.下列说法错误的是
A. 他家到公交车站台需行 千米
B. 他等公交车的时间为 分钟
C. 公交车的速度是 米/分
D. 他步行与乘公交车行驶的平均速度是 米/分
5. 已知 可以写成一个完全平方式,则 可为
A. B. C. D.
6. 如图,大小两个正方形在同一水平线上,小正方形从①的位置开始,匀速向右平移,到③的位置停止运动.如果设运动时间为 ,大小正方形重叠部分的面积为 ,则下列图象中,能表示 与 的函数关系的图象大致是
A. B.
C. D.
7. 如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温 随时间 变化而变化的关系,观察图象得到下列信息,其中错误的是
A. 凌晨4时气温最低为
B. 14时气温最高为
C. 从0时至14时,气温随时间增长而上升
D. 从14时至24时,气温随时间增长而下降
8. 如果一个 角的两条边与 的两条边分别平行,则 为
A. B. C. 或 D. 或
9. 园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积 与工作时间 的函数关系的图象如图,则休息后园林队每小时绿化面积为
A. B. C. D.
10. 如图,在边长为 的正方形 中剪去一个边长为 的小正方形 ,动点 从 出发,沿 的路线绕多边形的边匀速运动到点 时停止(不含点 和点 ),则 的面积 随着时间 变化的函数图象大致为
A. B.
C. D.
11. 若等腰三角形中有一个角等于 ,则这个等腰三角形的顶角的度数为
A. B. C. 或 D. 或
12. 如图 所示,甲、乙两车沿直路同向行驶,车速分别为 和 ,起初甲车在乙车前 处,两车同时出发,当乙车追上甲车时,两车都停止行驶.设 后两车相距 , 与 的函数关系如图 所示.有以下结论:
①图 中 的值为 ;
②乙车的速度为 ;
③图 中线段 应表示为 ;
④图 中函数图象与 轴交点的横坐标为 .
其中所有的正确结论是
A. ①④ B. ②③ C. ①②④ D. ①③④
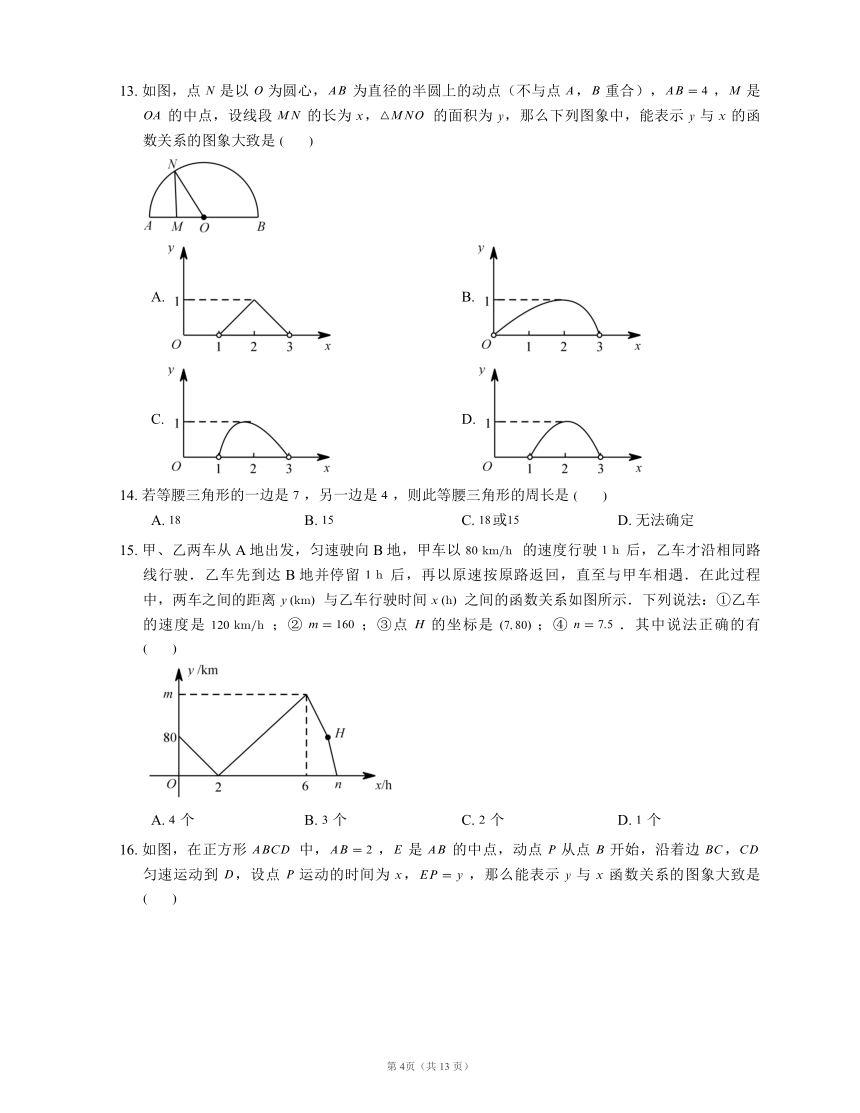
13. 如图,点 是以 为圆心, 为直径的半圆上的动点(不与点 , 重合),, 是 的中点,设线段 的长为 , 的面积为 ,那么下列图象中,能表示 与 的函数关系的图象大致是
A. B.
C. D.
14. 若等腰三角形的一边是 ,另一边是 ,则此等腰三角形的周长是
A. B. C. 或 D. 无法确定
15. 甲、乙两车从A地出发,匀速驶向B地,甲车以 的速度行驶 后,乙车才沿相同路线行驶.乙车先到达B地并停留 后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离 与乙车行驶时间 之间的函数关系如图所示.下列说法:①乙车的速度是 ;② ;③点 的坐标是 ;④ .其中说法正确的有
A. 个 B. 个 C. 个 D. 个
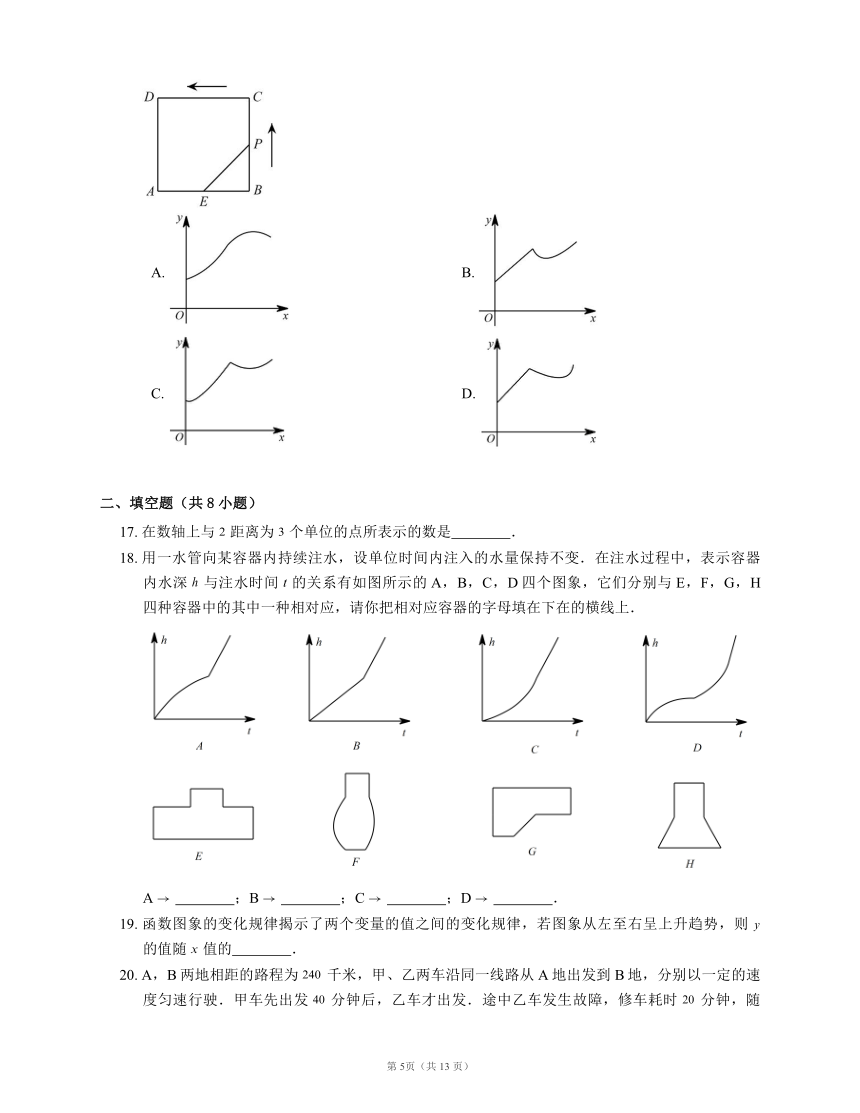
16. 如图,在正方形 中,, 是 的中点,动点 从点 开始,沿着边 , 匀速运动到 ,设点 运动的时间为 ,,那么能表示 与 函数关系的图象大致是
A. B.
C. D.
二、填空题(共8小题)
17. 在数轴上与 距离为 个单位的点所表示的数是 ?.
18. 用一水管向某容器内持续注水,设单位时间内注入的水量保持不变.在注水过程中,表示容器内水深 与注水时间 的关系有如图所示的A,B,C,D四个图象,它们分别与E,F,G,H四种容器中的其中一种相对应,请你把相对应容器的字母填在下在的横线上.
A ?;B ?;C ?;D ?.
19. 函数图象的变化规律揭示了两个变量的值之间的变化规律,若图象从左至右呈上升趋势,则 的值随 值的 ?.
20. A,B两地相距的路程为 千米,甲、乙两车沿同一线路从A地出发到B地,分别以一定的速度匀速行驶.甲车先出发 分钟后,乙车才出发.途中乙车发生故障,修车耗时 分钟,随后,乙车车速比发生故障前减少了 千米/小时(仍保持匀速前行),甲、乙两车同时到达B地.甲、乙两车相距的路程 (千米)与甲车行驶时间 (小时)之间的关系如图所示,求乙车修好时,甲车距B地还有 ?千米.
21. 书店举行购书优惠活动:① 一次性购书不超过 元,不享受打折优惠;② 一次性购书超过 元但不超过 元,一律按原价打九折;③ 一次性购书超过 元,一律按原价打七折.小丽在这次活动中,两次购书总共付款 元,第二次购书原价是第一次购书原价的 倍,那么小丽这两次购书原价的总和是 ? 元.
22. 如图,在平面直角坐标系中,函数 和 的图象分别为直线 ,,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,,依次进行下去,则点 的坐标为 ?.
23. 一天早晨,小玲从家出发匀速步行到学校.小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲.妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半.小玲继续以原速度步行前往学校.妈妈与小玲之间的距离 (米)与小玲从家出发后步行的时间 (分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为 ?米.
24. 在 中,,, 为 的中点,动点 从 点出发,以每秒 的速度沿 的方向运动.设运动时间为 ,那么当 ?秒时,过 , 两点的直线将 的周长分成两个部分,使其中一部分是另一部分的 倍.
三、解答题(共6小题)
25. 在某次流感传播期间,小明班上有 的同学感冒,小明周三早晨得流感并开始发烧,但小明吃了些药后坚持去上课(体温大于等于 时为发烧),请根据图回答:
(1)周三小明是几时开始发烧的?
(2)最高烧到多少摄氏度?
26. 已知 ,过不在直线 , 上的一点 作 于点 , 于点 ,且 是 的 倍少 ,试画图并求出 的度数.
27. 请按要求画出函数 的图象:
(1)列表;
(2)描点;
(3)连线;
(4)请你判断点 , 是否在函数图象上,答: ?.
28. 如图, 是半圆弧 上一动点,连接 ,,过圆心 作 交 于点 ,连接 .已知 ,设 , 两点间的距离为 ,, 两点间的距离为 .小东根据学习函数的经验,对函数 随自变量 的变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了 与 的几组值,如下表:(说明:补全表格时相关数据保留一位小数)
(2)建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:直接写出 周长 的取值范围是 ?.
29. 如图 ,一条笔直的公路上有 ,, 三地,, 两地相距 千米,甲、乙两辆汽车分别从 , 两地同时出发,沿公路始终匀速相向而行,分别驶往 , 两地.甲、乙两车到 地的距离 ,(千米)与行驶时间 (时)的关系如图 所示.
根据图象进行以下探究:
(1)请在图 中标出 地的位置,并写出相应的距离:
? , ? ;
(2)在图 中求出甲汽车到达 地的时间 ,并写出甲车从 地到 地与甲车从 地到 地的 与行驶时间 的关系式.
(3) 地设有指挥中心,指挥中心及两车都配有对讲机,对讲机在 千米之内(含 千米)时能够互相通话,请问两车至少有一辆车能与指挥中心用对讲机通话的时间一共有多长?写出过程.
30. 解不等式 .
答案
1. D
2. D 【解析】如图,
数轴上到 的距离是 的点表示的数是:,,
数轴上到 的距离是 的点表示的数是 或 .
3. C
4. D
5. B
6. C
7. C
8. C 【解析】 一个 角的两条边与 的两条边分别平行,
或 ,
的度数为 或 .
9. D
10. B
【解析】本题考察实际问题与一次函数的图象.当点 从点 向点 移动时 逐渐增加;当点 在 上移动时 不变;当点 在 上移动时 逐渐减小;当点 在 上移动时 不变;当点 在 上移动时 逐渐减小,符合此特征的函数图象为B.
11. D 【解析】答案:D
12. A
13. D
14. C
15. B
16. C 【解析】由题意可知:
从 , 的长度从 到 ,其对应的解析式为 ;可排除B、D选项;
从 到 的中点时, 长度由 变成 ;
从 的中点到 时, 长度由 变成 ;
在 上运动时,运动长度是对称的,运动长度先减小再增大,
可选择C.
17. 或
18. G,E,H,F
19. 增大而增大
20.
【解析】由题意可得,
甲车的速度为:(千米/时),
甲车从A地到B地用的时间为:(小时),
乙车刚开始的速度为:(千米/时),
乙车发生故障之后的速度为:(千米/时),
设乙车发生故障时,乙车已经行驶了 小时,
,
解得,,
乙车修好时,甲车行驶的时间为:(小时),
乙车修好时,甲车距B地还有:(千米).
21. 或
【解析】设第一次购书原价为 元,第二次购书原价为 元.
由题意知 .
若 ,则 .解得 .
故两次购书原价的总和是 元.
若 ,则 .解得 .
故两次购书原价的总和是 元.
若 ,则 .不符题意.
故答案为: 或 .
22.
【解析】观察并发现规律:,,,,,
( 为自然数).
,
的坐标为 .
23.
24. 或
【解析】
两种情况:
(1)当点 在 上时,由题意得 ,解得 ;
(2)当点 在 上时,由题意得 ,解得 .
25. (1) 时.
??????(2) .
26. ,
设 ,则 ,如图 ,
,
,
,则 ;
如图 ,
,
,
,则 ,
综上所述 .
27. (1) 列表;
??????(2) 描点,如图 所示;
??????(3) 连线,如图 所示;
??????(4) 点 在函数图象上,点 不在函数图象上.
28. (1)
??????(2)
??????(3)
29. (1) ;
??????(2) 由图可知甲汽车的速度:,
(小时).
当 时:,
当 时:.
??????(3) 由图可知,甲达到距离 地 内时,甲用时:
(小时).
甲离开 地距离 地 千米时,所用时间:
,
由图可知乙的速度为:.
乙达到距离 地 内时,乙用时:
(小时).
乙离开 地距离 千米时,所用时间:
(小时).
(小时) 分钟.
综上:两车至少有一辆车能与指挥中心用对讲机通话的时间一共有 分钟.
30. 当 时,不等式的解集为 ;当 时,不等式无解集.
一、选择题(共16小题)
1. 如果两个变量 , 之间的函数关系如图所示,则函数值 的取值范围是
A. B. C. D.
2. 数轴上到 的距离是 的点表示的数是
A. B. C. D. 或
3. 在 月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是
A. 月份 B. 月份 C. 月份 D. 月份
4. 小亮从家出发步行到公交站台后,等公交车去学校,如图,折线表示这个过程中行程 (千米)与所花时间 (分)之间的关系.下列说法错误的是
A. 他家到公交车站台需行 千米
B. 他等公交车的时间为 分钟
C. 公交车的速度是 米/分
D. 他步行与乘公交车行驶的平均速度是 米/分
5. 已知 可以写成一个完全平方式,则 可为
A. B. C. D.
6. 如图,大小两个正方形在同一水平线上,小正方形从①的位置开始,匀速向右平移,到③的位置停止运动.如果设运动时间为 ,大小正方形重叠部分的面积为 ,则下列图象中,能表示 与 的函数关系的图象大致是
A. B.
C. D.
7. 如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温 随时间 变化而变化的关系,观察图象得到下列信息,其中错误的是
A. 凌晨4时气温最低为
B. 14时气温最高为
C. 从0时至14时,气温随时间增长而上升
D. 从14时至24时,气温随时间增长而下降
8. 如果一个 角的两条边与 的两条边分别平行,则 为
A. B. C. 或 D. 或
9. 园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积 与工作时间 的函数关系的图象如图,则休息后园林队每小时绿化面积为
A. B. C. D.
10. 如图,在边长为 的正方形 中剪去一个边长为 的小正方形 ,动点 从 出发,沿 的路线绕多边形的边匀速运动到点 时停止(不含点 和点 ),则 的面积 随着时间 变化的函数图象大致为
A. B.
C. D.
11. 若等腰三角形中有一个角等于 ,则这个等腰三角形的顶角的度数为
A. B. C. 或 D. 或
12. 如图 所示,甲、乙两车沿直路同向行驶,车速分别为 和 ,起初甲车在乙车前 处,两车同时出发,当乙车追上甲车时,两车都停止行驶.设 后两车相距 , 与 的函数关系如图 所示.有以下结论:
①图 中 的值为 ;
②乙车的速度为 ;
③图 中线段 应表示为 ;
④图 中函数图象与 轴交点的横坐标为 .
其中所有的正确结论是
A. ①④ B. ②③ C. ①②④ D. ①③④
13. 如图,点 是以 为圆心, 为直径的半圆上的动点(不与点 , 重合),, 是 的中点,设线段 的长为 , 的面积为 ,那么下列图象中,能表示 与 的函数关系的图象大致是
A. B.
C. D.
14. 若等腰三角形的一边是 ,另一边是 ,则此等腰三角形的周长是
A. B. C. 或 D. 无法确定
15. 甲、乙两车从A地出发,匀速驶向B地,甲车以 的速度行驶 后,乙车才沿相同路线行驶.乙车先到达B地并停留 后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离 与乙车行驶时间 之间的函数关系如图所示.下列说法:①乙车的速度是 ;② ;③点 的坐标是 ;④ .其中说法正确的有
A. 个 B. 个 C. 个 D. 个
16. 如图,在正方形 中,, 是 的中点,动点 从点 开始,沿着边 , 匀速运动到 ,设点 运动的时间为 ,,那么能表示 与 函数关系的图象大致是
A. B.
C. D.
二、填空题(共8小题)
17. 在数轴上与 距离为 个单位的点所表示的数是 ?.
18. 用一水管向某容器内持续注水,设单位时间内注入的水量保持不变.在注水过程中,表示容器内水深 与注水时间 的关系有如图所示的A,B,C,D四个图象,它们分别与E,F,G,H四种容器中的其中一种相对应,请你把相对应容器的字母填在下在的横线上.
A ?;B ?;C ?;D ?.
19. 函数图象的变化规律揭示了两个变量的值之间的变化规律,若图象从左至右呈上升趋势,则 的值随 值的 ?.
20. A,B两地相距的路程为 千米,甲、乙两车沿同一线路从A地出发到B地,分别以一定的速度匀速行驶.甲车先出发 分钟后,乙车才出发.途中乙车发生故障,修车耗时 分钟,随后,乙车车速比发生故障前减少了 千米/小时(仍保持匀速前行),甲、乙两车同时到达B地.甲、乙两车相距的路程 (千米)与甲车行驶时间 (小时)之间的关系如图所示,求乙车修好时,甲车距B地还有 ?千米.
21. 书店举行购书优惠活动:① 一次性购书不超过 元,不享受打折优惠;② 一次性购书超过 元但不超过 元,一律按原价打九折;③ 一次性购书超过 元,一律按原价打七折.小丽在这次活动中,两次购书总共付款 元,第二次购书原价是第一次购书原价的 倍,那么小丽这两次购书原价的总和是 ? 元.
22. 如图,在平面直角坐标系中,函数 和 的图象分别为直线 ,,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,过点 作 轴的垂线交 于点 ,,依次进行下去,则点 的坐标为 ?.
23. 一天早晨,小玲从家出发匀速步行到学校.小玲出发一段时间后,她的妈妈发现小玲忘带了一件必需的学习用品,于是立即下楼骑自行车,沿小玲行进的路线,匀速去追小玲.妈妈追上小玲将学习用品交给小玲后,立即沿原路线匀速返回家里,但由于路上行人渐多,妈妈返回时骑车的速度只是原来速度的一半.小玲继续以原速度步行前往学校.妈妈与小玲之间的距离 (米)与小玲从家出发后步行的时间 (分)之间的关系如图所示(小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计).当妈妈刚回到家时,小玲离学校的距离为 ?米.
24. 在 中,,, 为 的中点,动点 从 点出发,以每秒 的速度沿 的方向运动.设运动时间为 ,那么当 ?秒时,过 , 两点的直线将 的周长分成两个部分,使其中一部分是另一部分的 倍.
三、解答题(共6小题)
25. 在某次流感传播期间,小明班上有 的同学感冒,小明周三早晨得流感并开始发烧,但小明吃了些药后坚持去上课(体温大于等于 时为发烧),请根据图回答:
(1)周三小明是几时开始发烧的?
(2)最高烧到多少摄氏度?
26. 已知 ,过不在直线 , 上的一点 作 于点 , 于点 ,且 是 的 倍少 ,试画图并求出 的度数.
27. 请按要求画出函数 的图象:
(1)列表;
(2)描点;
(3)连线;
(4)请你判断点 , 是否在函数图象上,答: ?.
28. 如图, 是半圆弧 上一动点,连接 ,,过圆心 作 交 于点 ,连接 .已知 ,设 , 两点间的距离为 ,, 两点间的距离为 .小东根据学习函数的经验,对函数 随自变量 的变化而变化的规律进行探究.下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了 与 的几组值,如下表:(说明:补全表格时相关数据保留一位小数)
(2)建立直角坐标系,描出以补全后的表中各对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:直接写出 周长 的取值范围是 ?.
29. 如图 ,一条笔直的公路上有 ,, 三地,, 两地相距 千米,甲、乙两辆汽车分别从 , 两地同时出发,沿公路始终匀速相向而行,分别驶往 , 两地.甲、乙两车到 地的距离 ,(千米)与行驶时间 (时)的关系如图 所示.
根据图象进行以下探究:
(1)请在图 中标出 地的位置,并写出相应的距离:
? , ? ;
(2)在图 中求出甲汽车到达 地的时间 ,并写出甲车从 地到 地与甲车从 地到 地的 与行驶时间 的关系式.
(3) 地设有指挥中心,指挥中心及两车都配有对讲机,对讲机在 千米之内(含 千米)时能够互相通话,请问两车至少有一辆车能与指挥中心用对讲机通话的时间一共有多长?写出过程.
30. 解不等式 .
答案
1. D
2. D 【解析】如图,
数轴上到 的距离是 的点表示的数是:,,
数轴上到 的距离是 的点表示的数是 或 .
3. C
4. D
5. B
6. C
7. C
8. C 【解析】 一个 角的两条边与 的两条边分别平行,
或 ,
的度数为 或 .
9. D
10. B
【解析】本题考察实际问题与一次函数的图象.当点 从点 向点 移动时 逐渐增加;当点 在 上移动时 不变;当点 在 上移动时 逐渐减小;当点 在 上移动时 不变;当点 在 上移动时 逐渐减小,符合此特征的函数图象为B.
11. D 【解析】答案:D
12. A
13. D
14. C
15. B
16. C 【解析】由题意可知:
从 , 的长度从 到 ,其对应的解析式为 ;可排除B、D选项;
从 到 的中点时, 长度由 变成 ;
从 的中点到 时, 长度由 变成 ;
在 上运动时,运动长度是对称的,运动长度先减小再增大,
可选择C.
17. 或
18. G,E,H,F
19. 增大而增大
20.
【解析】由题意可得,
甲车的速度为:(千米/时),
甲车从A地到B地用的时间为:(小时),
乙车刚开始的速度为:(千米/时),
乙车发生故障之后的速度为:(千米/时),
设乙车发生故障时,乙车已经行驶了 小时,
,
解得,,
乙车修好时,甲车行驶的时间为:(小时),
乙车修好时,甲车距B地还有:(千米).
21. 或
【解析】设第一次购书原价为 元,第二次购书原价为 元.
由题意知 .
若 ,则 .解得 .
故两次购书原价的总和是 元.
若 ,则 .解得 .
故两次购书原价的总和是 元.
若 ,则 .不符题意.
故答案为: 或 .
22.
【解析】观察并发现规律:,,,,,
( 为自然数).
,
的坐标为 .
23.
24. 或
【解析】
两种情况:
(1)当点 在 上时,由题意得 ,解得 ;
(2)当点 在 上时,由题意得 ,解得 .
25. (1) 时.
??????(2) .
26. ,
设 ,则 ,如图 ,
,
,
,则 ;
如图 ,
,
,
,则 ,
综上所述 .
27. (1) 列表;
??????(2) 描点,如图 所示;
??????(3) 连线,如图 所示;
??????(4) 点 在函数图象上,点 不在函数图象上.
28. (1)
??????(2)
??????(3)
29. (1) ;
??????(2) 由图可知甲汽车的速度:,
(小时).
当 时:,
当 时:.
??????(3) 由图可知,甲达到距离 地 内时,甲用时:
(小时).
甲离开 地距离 地 千米时,所用时间:
,
由图可知乙的速度为:.
乙达到距离 地 内时,乙用时:
(小时).
乙离开 地距离 千米时,所用时间:
(小时).
(小时) 分钟.
综上:两车至少有一辆车能与指挥中心用对讲机通话的时间一共有 分钟.
30. 当 时,不等式的解集为 ;当 时,不等式无解集.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
