人教六(上)第三单元《分数除法》课时7课件(21张PPT)
文档属性
| 名称 | 人教六(上)第三单元《分数除法》课时7课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-27 07:34:01 | ||
图片预览






文档简介
(共21张PPT)
分数除法
第7课时 分数和倍问题
人教版 数学 六年级 上册
1.使学生学会分数和倍问题的解题思路和方法。
2.提高学生用方程解答应用题的能力。
【重难点】归纳分数和倍问题的特点及解题思路,解决实际问题。
用含有x的式子口答下面问题。
樱花树有多少棵 ?
樱花树
校园里有樟树x棵,樱花树的棵数是樟树的。
樟树和樱花树一共有多少棵 ?
樟树比樱花树多多少棵 ?
樟树
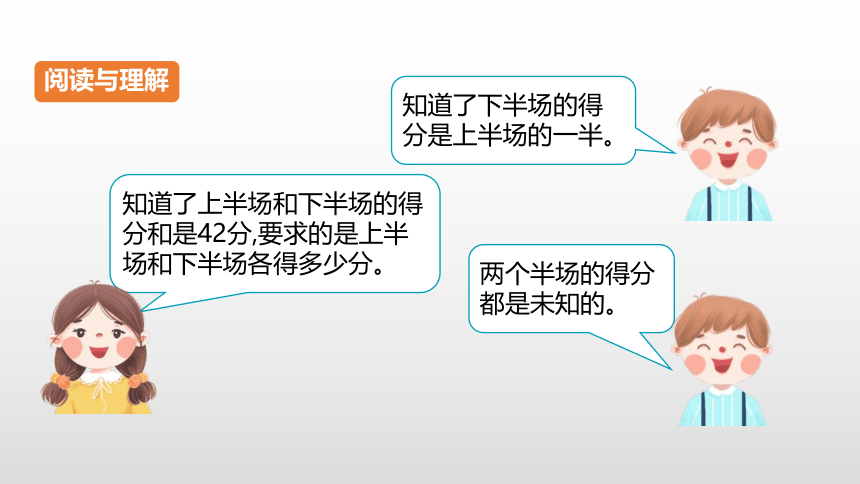
上半场和下半场各得多少分?
我们班全场
得了42分。
下半场得分只有上半场的一半。
知道了上半场和下半场的得分和是42分,要求的是上半场和下半场各得多少分。
阅读与理解
知道了下半场的得分是上半场的一半。
两个半场的得分都是未知的。
下半场得分是上半场的一半,也就是下半场得分=上半场得分。
分析与解答
也可以想成上半场得分是下半场的2倍。
解:设上半场得x 分。
设下半场得x 分。
x+2x=42
3x=42
x=42÷3
x=14
42-14=28(分)
或
或
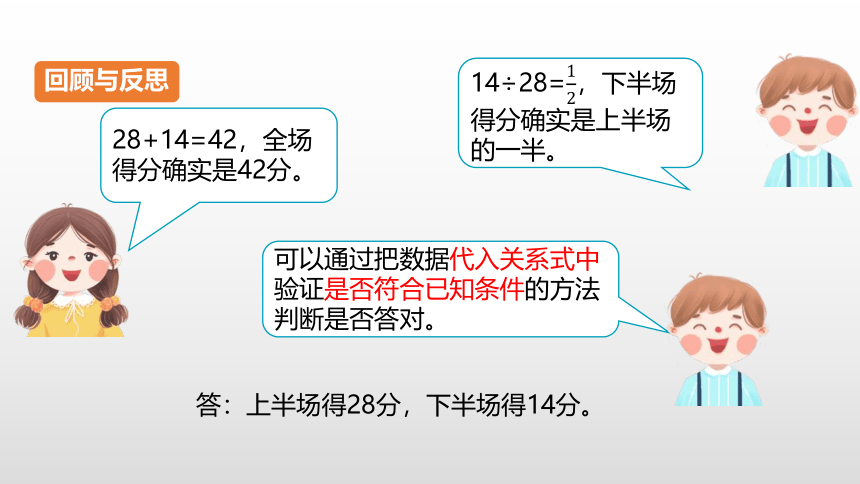
28+14=42,全场得分确实是42分。
回顾与反思
14÷28=,下半场得分确实是上半场的一半。
答:上半场得28分,下半场得14分。
可以通过把数据代入关系式中验证是否符合已知条件的方法判断是否答对。
回顾与反思
本题的已知条件是什么?
已知两个数的和与它们之间的倍数关系。
要求的是这两个数分别是多少。
本题要求的是什么?
回顾与反思
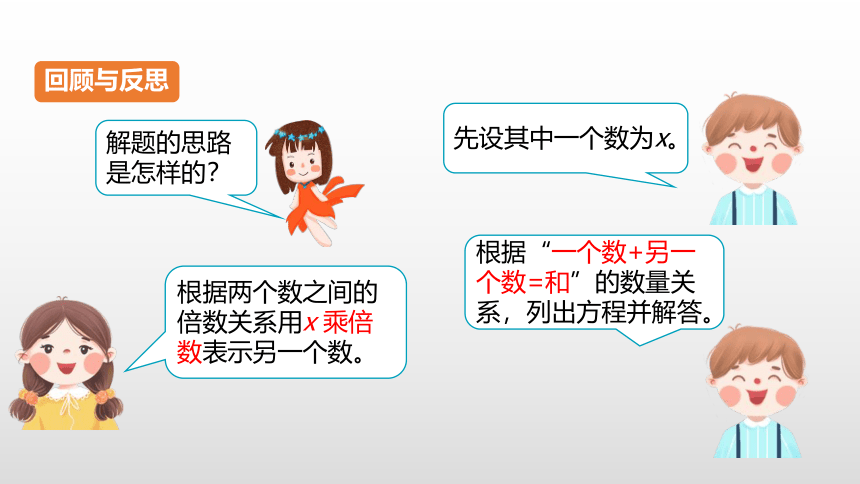
解题的思路是怎样的?
先设其中一个数为x。
根据“一个数+另一个数=和”的数量关系,列出方程并解答。
根据两个数之间的倍数关系用x 乘倍数表示另一个数。
回顾与反思
已知两个数的和以及它们之间的倍数关系,求这两个数是多少的问题,叫和倍问题。
和倍问题的关系式是:
和(倍数+1)=1倍数(单位“1”)
1倍数×倍数=几倍数
和-1倍数=几倍数
这道题用算术法怎样解答呢?
方法一:
下半场:
上半场:
14╳2=28(分)
42÷(1+2)=14(分)
方法二:
上半场:
下半场:
某电视机厂去年全年生产电视机108万台,其中上半年产量是下半年的。这个电视机厂去年上半年和下半年的产量分别是多少万台?
算术方法
列方程解答
和(倍数+1)=1倍数(单位“1”)
(万台)
(万台)
解:设下半年产量为x万台。
答:这个厂上半年的产量是48万台,
下半年的产量是60万台。
1
这套运动服共300元,裤子价钱是上衣的。
上衣和裤子的价钱分别是多少?
解:设上衣的价钱是x元。
(元)
答:上衣的价钱是180元,裤子的价钱是120元。
上衣的价钱╳=裤子的价钱。
2
航模小组和美术小组分别有多少人?
航模小组和美术小组一共有45人。
美术小组的人数是航模小组的。
解:设航模小组有x人。
(人)
答:航模小组有25人,美术小组有20人。
航模小组人数
美术小组人数
3
航模小组和美术小组分别有多少人?
解:设美术小组有x人。
(人)
答:航模小组有25人,美术小组有20人。
航模小组人数
美术小组人数
航模小组和美术小组一共有45人。
美术小组的人数是航模小组的。
3
武汉长江大桥全长1670m,其中引桥的长度是正桥的。这座大桥的正桥和引桥的长度分别是多少米?
引桥+正桥=桥的全长
解:设正桥长x米。
(米)
答:这座大桥的正桥是1156米,引桥是514米。
4
中国农历中的“夏至”是一年中白昼最长,黑夜最短的一天。这一天,北京的黑夜时间是白天时间的。白昼和黑夜分别是多少小时?
解:设白天时间为x 小时。
答:白昼是15小时,黑夜是9小时。
一天有24小时,即:白昼+黑夜=24小时
24-15=9(小时)
解:设黑夜时间为x 小时。
24-9=15(小时)
24-9=15(小时)
5
如右图,长方形的周长是30cm,宽和长各是多少?
长方形的宽是长的。
长方形的周长=(长+宽)×2
解:设长方形的长为x。
答:长方形的宽是5厘米,长是10厘米。
(厘米)
6
小明和小红共有图书20本,小红的图书
数量是小明的。他们各有多少本图书?
小明的图书是我的3倍。
解:设小红有x本书。
x+3x=20
4x =20
x =5
5×3=15(本)
解:设小明有x本书。
(本)
答:小明有15本书,小红有5本书。
7
果园里种的桃树比梨树少300棵,桃树的棵数是梨树的,两种树各种了多少棵?
桃树的棵数:
梨树的棵数:
300棵
?棵
梨树的棵数:
桃树的棵数:
450-300=150(棵)
答:桃树种了150棵,梨树种了450棵。
8
这节课你学会了什么?
解“分数除法的和倍问题”的方法:
1.方程法:设1倍数(单位“1”)为x,用x ×倍数表示几倍数,再根据“1倍数+几倍数=和”列出方程,然后解方程。
2.算术法:和÷(1+倍数)=1倍数(单位“1”)
超市卖出牛肉和猪肉共700kg,卖出的牛肉是
猪肉的。卖出的牛肉和猪肉各是多少千克?
分数除法
第7课时 分数和倍问题
人教版 数学 六年级 上册
1.使学生学会分数和倍问题的解题思路和方法。
2.提高学生用方程解答应用题的能力。
【重难点】归纳分数和倍问题的特点及解题思路,解决实际问题。
用含有x的式子口答下面问题。
樱花树有多少棵 ?
樱花树
校园里有樟树x棵,樱花树的棵数是樟树的。
樟树和樱花树一共有多少棵 ?
樟树比樱花树多多少棵 ?
樟树
上半场和下半场各得多少分?
我们班全场
得了42分。
下半场得分只有上半场的一半。
知道了上半场和下半场的得分和是42分,要求的是上半场和下半场各得多少分。
阅读与理解
知道了下半场的得分是上半场的一半。
两个半场的得分都是未知的。
下半场得分是上半场的一半,也就是下半场得分=上半场得分。
分析与解答
也可以想成上半场得分是下半场的2倍。
解:设上半场得x 分。
设下半场得x 分。
x+2x=42
3x=42
x=42÷3
x=14
42-14=28(分)
或
或
28+14=42,全场得分确实是42分。
回顾与反思
14÷28=,下半场得分确实是上半场的一半。
答:上半场得28分,下半场得14分。
可以通过把数据代入关系式中验证是否符合已知条件的方法判断是否答对。
回顾与反思
本题的已知条件是什么?
已知两个数的和与它们之间的倍数关系。
要求的是这两个数分别是多少。
本题要求的是什么?
回顾与反思
解题的思路是怎样的?
先设其中一个数为x。
根据“一个数+另一个数=和”的数量关系,列出方程并解答。
根据两个数之间的倍数关系用x 乘倍数表示另一个数。
回顾与反思
已知两个数的和以及它们之间的倍数关系,求这两个数是多少的问题,叫和倍问题。
和倍问题的关系式是:
和(倍数+1)=1倍数(单位“1”)
1倍数×倍数=几倍数
和-1倍数=几倍数
这道题用算术法怎样解答呢?
方法一:
下半场:
上半场:
14╳2=28(分)
42÷(1+2)=14(分)
方法二:
上半场:
下半场:
某电视机厂去年全年生产电视机108万台,其中上半年产量是下半年的。这个电视机厂去年上半年和下半年的产量分别是多少万台?
算术方法
列方程解答
和(倍数+1)=1倍数(单位“1”)
(万台)
(万台)
解:设下半年产量为x万台。
答:这个厂上半年的产量是48万台,
下半年的产量是60万台。
1
这套运动服共300元,裤子价钱是上衣的。
上衣和裤子的价钱分别是多少?
解:设上衣的价钱是x元。
(元)
答:上衣的价钱是180元,裤子的价钱是120元。
上衣的价钱╳=裤子的价钱。
2
航模小组和美术小组分别有多少人?
航模小组和美术小组一共有45人。
美术小组的人数是航模小组的。
解:设航模小组有x人。
(人)
答:航模小组有25人,美术小组有20人。
航模小组人数
美术小组人数
3
航模小组和美术小组分别有多少人?
解:设美术小组有x人。
(人)
答:航模小组有25人,美术小组有20人。
航模小组人数
美术小组人数
航模小组和美术小组一共有45人。
美术小组的人数是航模小组的。
3
武汉长江大桥全长1670m,其中引桥的长度是正桥的。这座大桥的正桥和引桥的长度分别是多少米?
引桥+正桥=桥的全长
解:设正桥长x米。
(米)
答:这座大桥的正桥是1156米,引桥是514米。
4
中国农历中的“夏至”是一年中白昼最长,黑夜最短的一天。这一天,北京的黑夜时间是白天时间的。白昼和黑夜分别是多少小时?
解:设白天时间为x 小时。
答:白昼是15小时,黑夜是9小时。
一天有24小时,即:白昼+黑夜=24小时
24-15=9(小时)
解:设黑夜时间为x 小时。
24-9=15(小时)
24-9=15(小时)
5
如右图,长方形的周长是30cm,宽和长各是多少?
长方形的宽是长的。
长方形的周长=(长+宽)×2
解:设长方形的长为x。
答:长方形的宽是5厘米,长是10厘米。
(厘米)
6
小明和小红共有图书20本,小红的图书
数量是小明的。他们各有多少本图书?
小明的图书是我的3倍。
解:设小红有x本书。
x+3x=20
4x =20
x =5
5×3=15(本)
解:设小明有x本书。
(本)
答:小明有15本书,小红有5本书。
7
果园里种的桃树比梨树少300棵,桃树的棵数是梨树的,两种树各种了多少棵?
桃树的棵数:
梨树的棵数:
300棵
?棵
梨树的棵数:
桃树的棵数:
450-300=150(棵)
答:桃树种了150棵,梨树种了450棵。
8
这节课你学会了什么?
解“分数除法的和倍问题”的方法:
1.方程法:设1倍数(单位“1”)为x,用x ×倍数表示几倍数,再根据“1倍数+几倍数=和”列出方程,然后解方程。
2.算术法:和÷(1+倍数)=1倍数(单位“1”)
超市卖出牛肉和猪肉共700kg,卖出的牛肉是
猪肉的。卖出的牛肉和猪肉各是多少千克?
