人教六(上)第9单元 总复习 课时2课件(20张PPT)
文档属性
| 名称 | 人教六(上)第9单元 总复习 课时2课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 420.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-27 07:58:22 | ||
图片预览





文档简介
(共20张PPT)
人教版 数学 六年级 上册
数与代数(二)— 比
总复习第二节
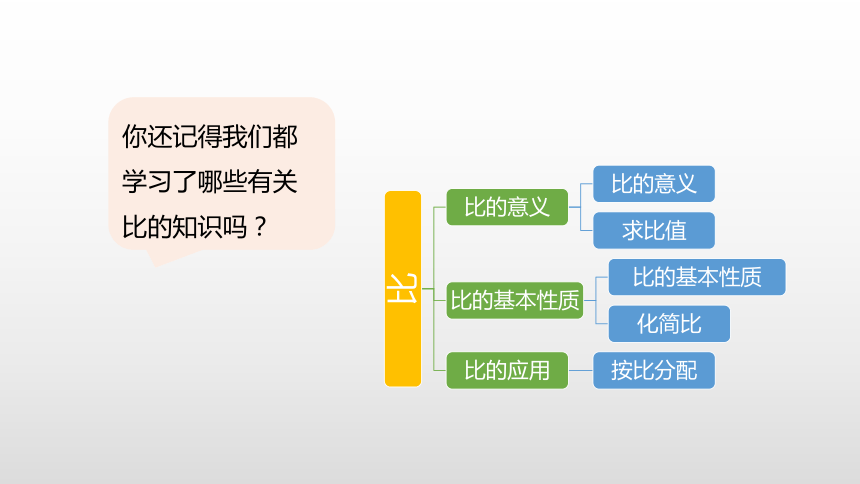
你还记得我们都学习了哪些有关比的知识吗?
①3∶7=( )÷( )=。
②书法小组有男生6人,女生5人,男女生人数的比是( );
女生人数和男生人数的比是( );男生和全小组人数的比
是( );女生和全小组人数的比是( )。
3
7
7
3
6 :5
5 :6
6:11
5:11
(一)比的意义
填一填。(课件出示)
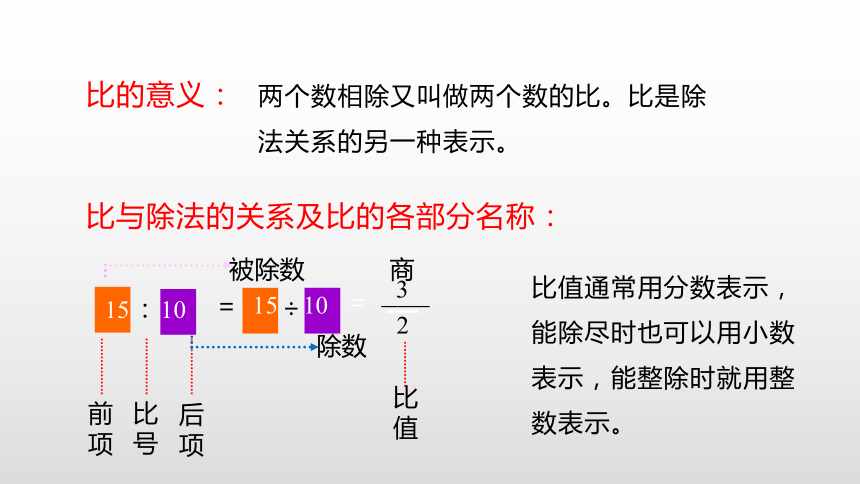
两个数相除又叫做两个数的比。比是除法关系的另一种表示。
比与除法的关系及比的各部分名称:
比
号
15 10
:
=
15 10
÷
=
2
3
前
项
后
项
比
值
被除数
除数
商
比的意义:
比值通常用分数表示,能除尽时也可以用小数表示,能整除时就用整数表示。
———
比
除法
分数
联 系
前项
被除数
分子
:比号
÷(除号)
—(分数线)
后项
除数
分母
比值
商
分数值
区别
一种关系
一种运算
一种数
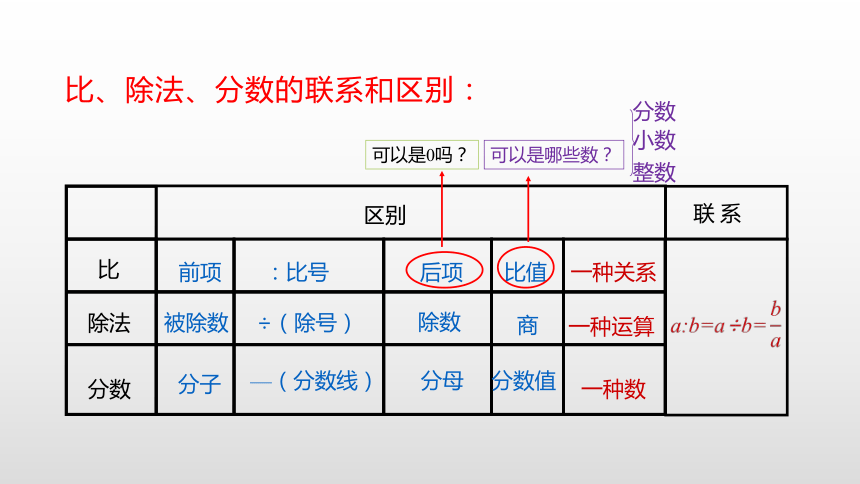
比、除法、分数的联系和区别:
可以是0吗?
可以是哪些数?
分数
小数
整数
比的前项和后项同时乘或除以相同的数,(0除外),比值不变。应用比的基本性质,我们可以把比化成最简单的整数比。
(二)比的基本性质
①根据比求出总份数。
②求出各部分数占总数的几分之几。
③运用分数乘法列式计算,求出各部分的量。
(三)比的应用(按比分配)
④化简比。
比的基本性质:比的前项和后项同时乘或除以相同的数(0 除外),比值不变。
根据比的基本性质,可以把比化成最简单的整数比。
(三)比的应用(按比分配)
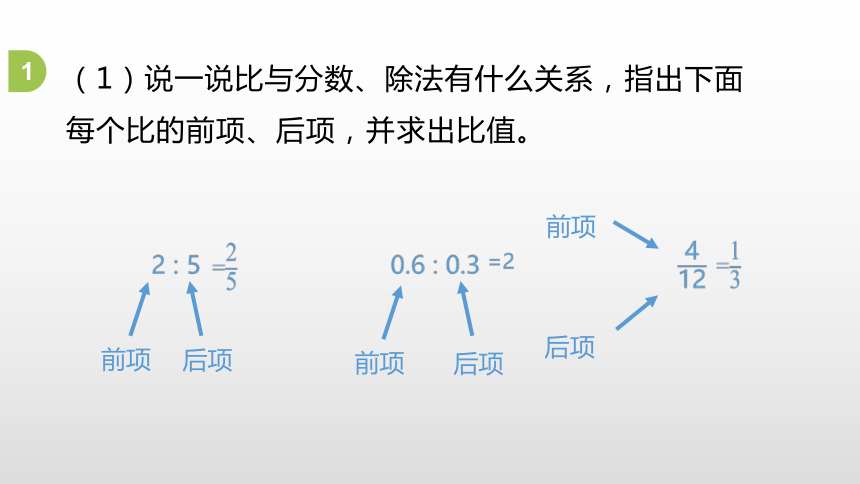
(1)说一说比与分数、除法有什么关系,指出下面每个比的前项、后项,并求出比值。
2 : 5 0.6 : 0.3
前项
后项
前项
后项
前项
后项
=
=
=
1
(2)化简下列各比。
180 : 120
= (15÷5) : (10÷5)
= 3 : 2
= (180÷60 ) : (120÷60 )
=3 : 2
1
15 : 10
一件衬衣售价为100 元,一条长裤的价钱和这件衬衣的价钱之比是3 : 2。这条长裤售价是多少元?
根据题意可知,一条长裤的价钱是一件衬衣价钱的,
所以长裤的价钱为
(元)
答:这条长裤售价是150元。
2
长方形的长为:
(cm)
答:这个长方形的长和宽分别是28cm和14cm。
长方形的宽为:
4(cm)
长、宽之和为:84÷2=42(cm)
方法一:
用84 cm 长的铁丝围成一个长方形,这个长方形的长与宽的比是2 : 1。这个长方形的长与宽分别是多少厘米?
3
用84 cm 长的铁丝围成一个长方形,这个长方形的长与宽的比是2 : 1。这个长方形的长与宽分别是多少厘米?
长方形的长为:
(cm)
长方形的宽为:
4(cm)
长、宽之和为:84÷2=42(cm)
42÷3=14(cm)
答:这个长方形的长和宽分别是28cm和14cm。
3
方法二:
先求每一份是多长:84÷(3+4+5)=7(cm)
三边长分别为:7×3=21(cm)
7×4=28(cm)
7×5=35(cm)
答:三条边各是21厘米、28厘米、35厘米。
用84 cm 长的铁丝围成一个三角形,这个三角形三条边长度的比是3 : 4 : 5。三条边各是多少厘米?
4
方法一:
用84 cm 长的铁丝围成一个三角形,这个三角形三条边长度的比是3 : 4 : 5。三条边各是多少厘米?
根据题意可知三角形的各边分别占周长的。
三边长分别为:84×=21(cm)
84×=28(cm)
84×=35(cm)
答:三条边各是21厘米、28厘米、35厘米。
4
方法二:
小明和爷爷的年龄比是1:6,已知小明比爷爷小50岁。小明和爷爷的年龄和是多少岁?
1+6=7
50÷(-)
=50÷
=70(岁)
答:小明和爷爷的年龄和是70岁。
5
(1)30mL的原液要加入多少毫升水?
30×6=180(mL)
答:要加入180毫升水。
要按照原汁:水=1:6的比把高浓缩橙汁原液配制成普通橙汁。
6
要按照原汁:水=1:6的比把高浓缩橙汁原液配制成普通橙汁。
(2)要配制3500mL普通橙汁,需要多少毫升的高浓缩原汁?
1+6=7
3500÷7=500(mL)
答:需要500mL的高浓缩原汁。
6
22000-1000=21000(元)
5+4+7+5=21
甲:
乙:
21000×=5000(元)
21000× =4000(元)
7
甲、乙、丙、丁四个家庭共存款22000元,其中甲、乙、丙三个家庭存款数的比是5:4:7。甲家庭比丁家庭的存款数多1000元,这四个家庭各有多少元的存款?
甲、乙、丙、丁四个家庭共存款22000元,其中甲、乙、丙三个家庭存款数的比是5:4:7。甲家庭比丁家庭的存款数多1000元,这四个家庭各有多少元的存款?
22000-1000=21000(元)
5+4+7+5=21
丙:
丁:
21000×=7000(元)
21000×+1000=6000(元)
答:这四个家庭各有5000元、4000元、7000元、6000元的存款。
7
人教版 数学 六年级 上册
数与代数(二)— 比
总复习第二节
你还记得我们都学习了哪些有关比的知识吗?
①3∶7=( )÷( )=。
②书法小组有男生6人,女生5人,男女生人数的比是( );
女生人数和男生人数的比是( );男生和全小组人数的比
是( );女生和全小组人数的比是( )。
3
7
7
3
6 :5
5 :6
6:11
5:11
(一)比的意义
填一填。(课件出示)
两个数相除又叫做两个数的比。比是除法关系的另一种表示。
比与除法的关系及比的各部分名称:
比
号
15 10
:
=
15 10
÷
=
2
3
前
项
后
项
比
值
被除数
除数
商
比的意义:
比值通常用分数表示,能除尽时也可以用小数表示,能整除时就用整数表示。
———
比
除法
分数
联 系
前项
被除数
分子
:比号
÷(除号)
—(分数线)
后项
除数
分母
比值
商
分数值
区别
一种关系
一种运算
一种数
比、除法、分数的联系和区别:
可以是0吗?
可以是哪些数?
分数
小数
整数
比的前项和后项同时乘或除以相同的数,(0除外),比值不变。应用比的基本性质,我们可以把比化成最简单的整数比。
(二)比的基本性质
①根据比求出总份数。
②求出各部分数占总数的几分之几。
③运用分数乘法列式计算,求出各部分的量。
(三)比的应用(按比分配)
④化简比。
比的基本性质:比的前项和后项同时乘或除以相同的数(0 除外),比值不变。
根据比的基本性质,可以把比化成最简单的整数比。
(三)比的应用(按比分配)
(1)说一说比与分数、除法有什么关系,指出下面每个比的前项、后项,并求出比值。
2 : 5 0.6 : 0.3
前项
后项
前项
后项
前项
后项
=
=
=
1
(2)化简下列各比。
180 : 120
= (15÷5) : (10÷5)
= 3 : 2
= (180÷60 ) : (120÷60 )
=3 : 2
1
15 : 10
一件衬衣售价为100 元,一条长裤的价钱和这件衬衣的价钱之比是3 : 2。这条长裤售价是多少元?
根据题意可知,一条长裤的价钱是一件衬衣价钱的,
所以长裤的价钱为
(元)
答:这条长裤售价是150元。
2
长方形的长为:
(cm)
答:这个长方形的长和宽分别是28cm和14cm。
长方形的宽为:
4(cm)
长、宽之和为:84÷2=42(cm)
方法一:
用84 cm 长的铁丝围成一个长方形,这个长方形的长与宽的比是2 : 1。这个长方形的长与宽分别是多少厘米?
3
用84 cm 长的铁丝围成一个长方形,这个长方形的长与宽的比是2 : 1。这个长方形的长与宽分别是多少厘米?
长方形的长为:
(cm)
长方形的宽为:
4(cm)
长、宽之和为:84÷2=42(cm)
42÷3=14(cm)
答:这个长方形的长和宽分别是28cm和14cm。
3
方法二:
先求每一份是多长:84÷(3+4+5)=7(cm)
三边长分别为:7×3=21(cm)
7×4=28(cm)
7×5=35(cm)
答:三条边各是21厘米、28厘米、35厘米。
用84 cm 长的铁丝围成一个三角形,这个三角形三条边长度的比是3 : 4 : 5。三条边各是多少厘米?
4
方法一:
用84 cm 长的铁丝围成一个三角形,这个三角形三条边长度的比是3 : 4 : 5。三条边各是多少厘米?
根据题意可知三角形的各边分别占周长的。
三边长分别为:84×=21(cm)
84×=28(cm)
84×=35(cm)
答:三条边各是21厘米、28厘米、35厘米。
4
方法二:
小明和爷爷的年龄比是1:6,已知小明比爷爷小50岁。小明和爷爷的年龄和是多少岁?
1+6=7
50÷(-)
=50÷
=70(岁)
答:小明和爷爷的年龄和是70岁。
5
(1)30mL的原液要加入多少毫升水?
30×6=180(mL)
答:要加入180毫升水。
要按照原汁:水=1:6的比把高浓缩橙汁原液配制成普通橙汁。
6
要按照原汁:水=1:6的比把高浓缩橙汁原液配制成普通橙汁。
(2)要配制3500mL普通橙汁,需要多少毫升的高浓缩原汁?
1+6=7
3500÷7=500(mL)
答:需要500mL的高浓缩原汁。
6
22000-1000=21000(元)
5+4+7+5=21
甲:
乙:
21000×=5000(元)
21000× =4000(元)
7
甲、乙、丙、丁四个家庭共存款22000元,其中甲、乙、丙三个家庭存款数的比是5:4:7。甲家庭比丁家庭的存款数多1000元,这四个家庭各有多少元的存款?
甲、乙、丙、丁四个家庭共存款22000元,其中甲、乙、丙三个家庭存款数的比是5:4:7。甲家庭比丁家庭的存款数多1000元,这四个家庭各有多少元的存款?
22000-1000=21000(元)
5+4+7+5=21
丙:
丁:
21000×=7000(元)
21000×+1000=6000(元)
答:这四个家庭各有5000元、4000元、7000元、6000元的存款。
7
