鲁教版 九年级下册数学 5.5 确定圆的条件(共23张ppt)
文档属性
| 名称 | 鲁教版 九年级下册数学 5.5 确定圆的条件(共23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 782.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-24 16:46:07 | ||
图片预览



文档简介
课件23张PPT。 导入新课怎样把圆柱形原木锯成截面为正方形的木材,并使截面正方形的面积尽可能地大?第五章圆
5.确定圆的条件(第2课时)学习目标知识目标 1. 理解圆内接四边形的概念,
掌握圆内接 四边形的性质定理;
2. 学会运用圆内接四边形的性质定理证明和计算一些问题能力目标培养学生观察、分析、概括的能力情感态度和
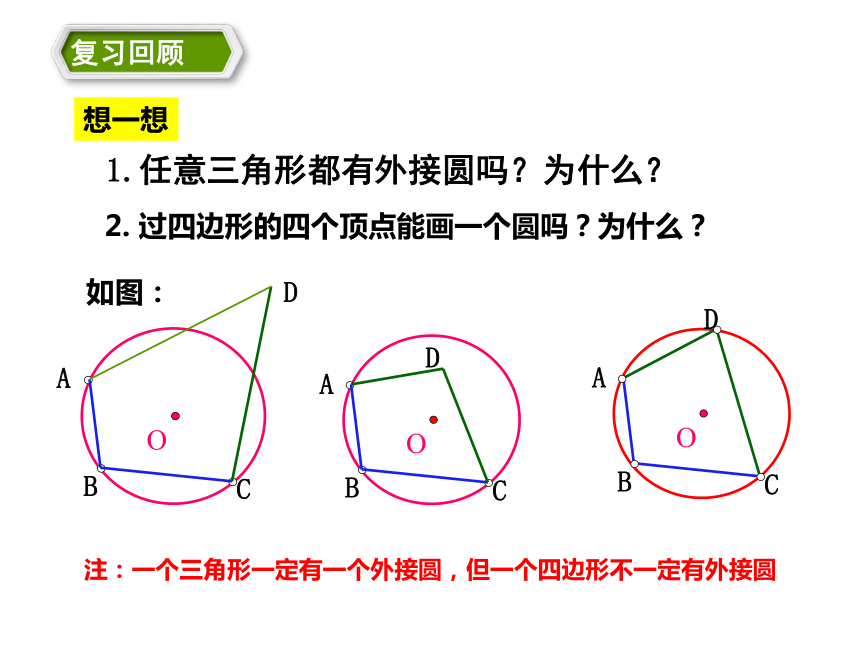
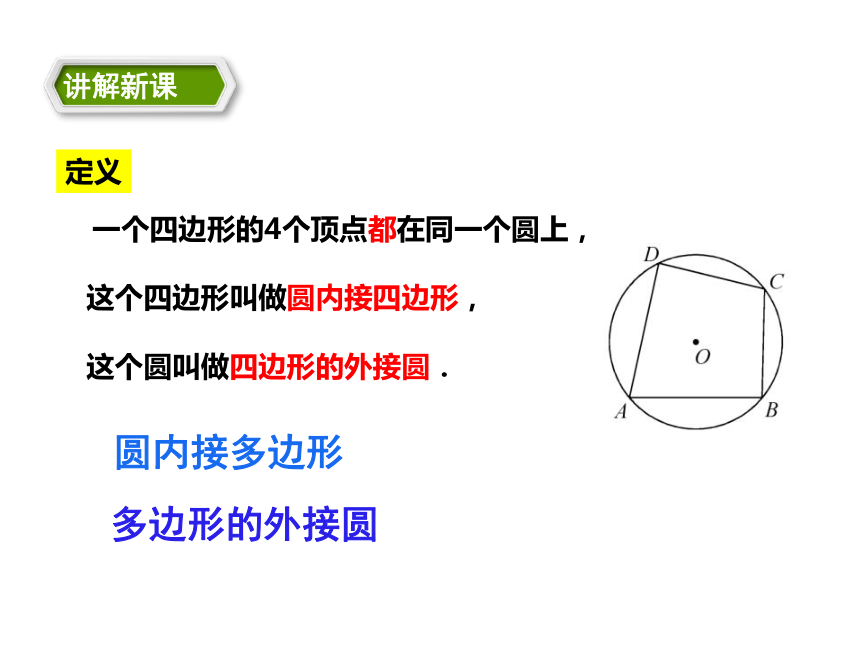
价值观目标充分发挥学生的主体作用,激发学生的探究的热情 2. 过四边形的四个顶点能画一个圆吗?为什么?想一想注:一个三角形一定有一个外接圆,但一个四边形不一定有外接圆1.任意三角形都有外接圆吗?为什么? 一个四边形的4个顶点都在同一个圆上,
这个四边形叫做圆内接四边形,
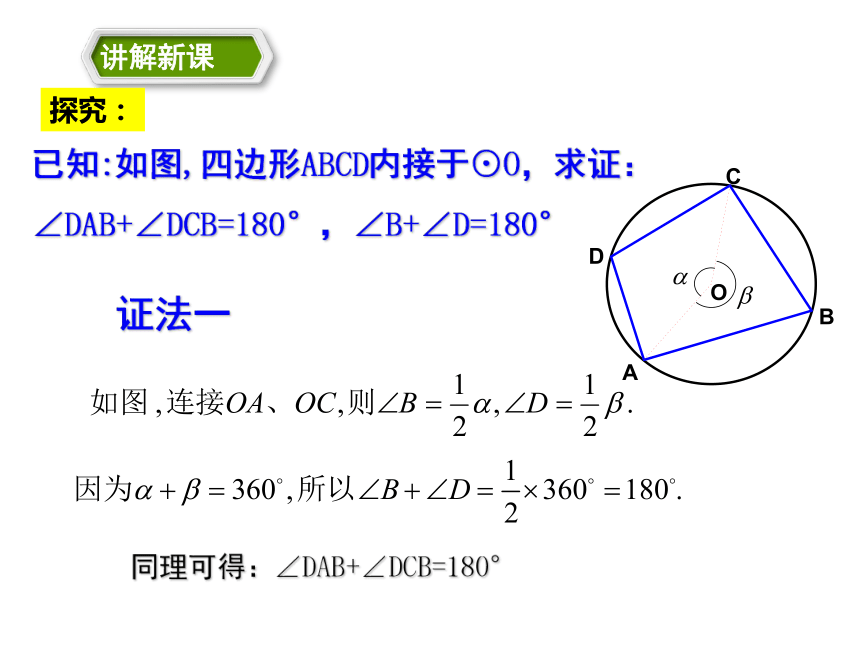
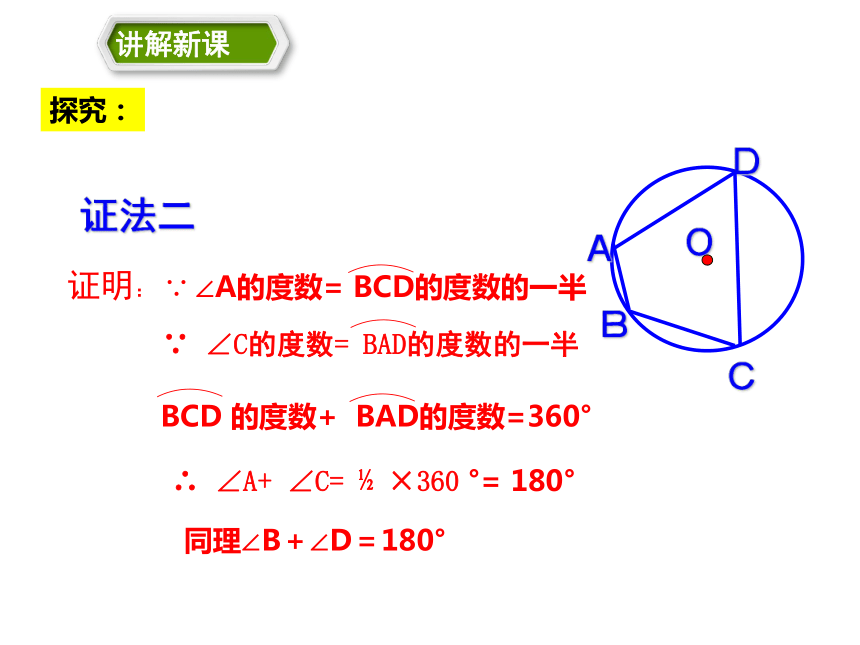
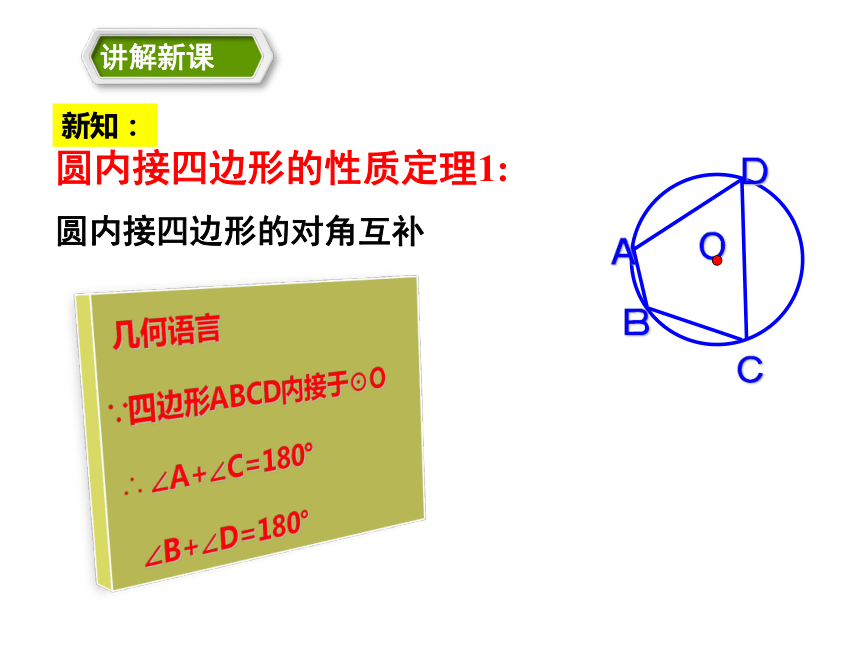
这个圆叫做四边形的外接圆. 定义圆内接多边形多边形的外接圆任意画一个圆,在圆上依次取四个点A、B、C、D,连接AB、BC、CD、DA,用量角器量出一组对角的度数之和,你发现了什么?与同伴交流一下合作学习发现:每一组对角相加等于180°,即对角互补。证法一已知:如图,四边形ABCD内接于⊙O,求证:∠DAB+∠DCB=180°,∠B+∠D=180°同理可得:∠DAB+∠DCB=180°探究:证法二探究:圆内接四边形的性质定理1:
圆内接四边形的对角互补新知: 几何语言
∵四边形ABCD内接于⊙O
∴ ∠A+∠C=180°
∠B+∠D=180°1、如图,AB为⊙O的直径,已知∠BAC=40°, 则∠D= _____ 2、圆内接四边形ABCD中,∠A:∠B:∠C=2:3:7,
则∠A=____∠B= ___∠C= __∠D=____小试牛刀:3、若四边形ABCD为圆内接四边形,则下列哪个选项成立( )(A)∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4 (B)∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4 (C)∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4 (D)∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1B130°40°60°140°120°4、四边形ABCD内接于⊙O,则∠A+∠C=______
∠B+∠ADC=_______;
若∠B=80°,
则∠ADC=______ ,
∠CDE=_________.180°180°100°80°O小试牛刀:新知:圆内接四边形的性质定理2:圆内接四边形的任何一个
外角都等于它的内对角。FM如图,△ABC的外角平分线AD交外接圆于D,求证:DB=DC.解:∵ AD是∠EAC的平分线∴∠DAE=∠DAC
∵ 四边形ABCD内接于⊙O
∴∠DAE=∠DCB
∴而∠DBC=∠DAC
∴∠DBC=∠DCB
∴ DB=DC探索例题如图,四边形ABCD内接于⊙O,并且AD是⊙O的直径,C是弧BD的中点,AB和DC的延长线交⊙O外一点E。求证:BC=EC.巩固练习:如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?最大横截面面积是多少?分析:要使锯出的木材的横截面正方形ABCD尽可能地
大,正方形ABCD应内接于☉O.
由正方形ABCD四个内角都是直角,得它的两条对角线是☉O的两条直径,且这两条直径互相垂直.
所以只要在☉O内作两条互相垂直的直径AC和BD,就可以作出☉O的内接正方形ABCD.大展身手:大展身手:如图所示, ⊙O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交⊙O于点D,连接 BD,DC.
求证:BD=DC=DI证明:∵AI 平分∠BAC,
∴∠BAD=∠DAC,
∴弧BD=弧BC
∴BD=DC.
∵BI 平分∠ABC,
∴∠ABI=∠CBI.
∵∠BAD=∠DAC,∠DBC=∠DAC,
∴∠BAD=∠DBC.
又∵∠DBI=∠DBC+∠CBI,∠DIB=∠ABI+∠BAD,
∴∠DBI=∠DIB,
∴△BDI为等腰三角形,
∴BD=ID,
∴BD=DC=DI. 知识……方法……感悟……1.已知,四边形ABCD是⊙O的内接四边形,∠D=50°,则∠ABC等于( )
A.100° B.110° C.120° D.130°
2.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.l05° C.100° D.95°DB3、如图,四边形ABCD是⊙O的内接四边形,∠B=130°,则∠AOC的度数是__ _度.1004、如图,点A,B,C,D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是____ .5、如图,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P,∠P=30°,∠ABC=100°,则∠C= 。?70°“方”是做人之本,是堂堂正正做人的脊梁,“圆”是处世之道,是妥妥当当处世的锦囊。一个人,如果过分方正,有棱有角,难免碰得头破血流;而一个人如果八面玲珑,圆滑透顶,总想自己占便宜,也必将众叛亲离。因此,做人必须方外有圆,圆内有方。
掌握圆内接 四边形的性质定理;
2. 学会运用圆内接四边形的性质定理证明和计算一些问题能力目标培养学生观察、分析、概括的能力情感态度和
价值观目标充分发挥学生的主体作用,激发学生的探究的热情 2. 过四边形的四个顶点能画一个圆吗?为什么?想一想注:一个三角形一定有一个外接圆,但一个四边形不一定有外接圆1.任意三角形都有外接圆吗?为什么? 一个四边形的4个顶点都在同一个圆上,
这个四边形叫做圆内接四边形,
这个圆叫做四边形的外接圆. 定义圆内接多边形多边形的外接圆任意画一个圆,在圆上依次取四个点A、B、C、D,连接AB、BC、CD、DA,用量角器量出一组对角的度数之和,你发现了什么?与同伴交流一下合作学习发现:每一组对角相加等于180°,即对角互补。证法一已知:如图,四边形ABCD内接于⊙O,求证:∠DAB+∠DCB=180°,∠B+∠D=180°同理可得:∠DAB+∠DCB=180°探究:证法二探究:圆内接四边形的性质定理1:
圆内接四边形的对角互补新知: 几何语言
∵四边形ABCD内接于⊙O
∴ ∠A+∠C=180°
∠B+∠D=180°1、如图,AB为⊙O的直径,已知∠BAC=40°, 则∠D= _____ 2、圆内接四边形ABCD中,∠A:∠B:∠C=2:3:7,
则∠A=____∠B= ___∠C= __∠D=____小试牛刀:3、若四边形ABCD为圆内接四边形,则下列哪个选项成立( )(A)∠A∶∠B∶∠C∶∠D = 1∶2∶3∶4 (B)∠A∶∠B∶∠C∶∠D = 2∶1∶3∶4 (C)∠A∶∠B∶∠C∶∠D = 3∶2∶1∶4 (D)∠A∶∠B∶∠C∶∠D = 4∶3∶2∶1B130°40°60°140°120°4、四边形ABCD内接于⊙O,则∠A+∠C=______
∠B+∠ADC=_______;
若∠B=80°,
则∠ADC=______ ,
∠CDE=_________.180°180°100°80°O小试牛刀:新知:圆内接四边形的性质定理2:圆内接四边形的任何一个
外角都等于它的内对角。FM如图,△ABC的外角平分线AD交外接圆于D,求证:DB=DC.解:∵ AD是∠EAC的平分线∴∠DAE=∠DAC
∵ 四边形ABCD内接于⊙O
∴∠DAE=∠DCB
∴而∠DBC=∠DAC
∴∠DBC=∠DCB
∴ DB=DC探索例题如图,四边形ABCD内接于⊙O,并且AD是⊙O的直径,C是弧BD的中点,AB和DC的延长线交⊙O外一点E。求证:BC=EC.巩固练习:如果要把直径为30cm的圆柱形原木锯成一根横截面为正方形的木材,并使截面尽可能地大,应怎样锯?最大横截面面积是多少?分析:要使锯出的木材的横截面正方形ABCD尽可能地
大,正方形ABCD应内接于☉O.
由正方形ABCD四个内角都是直角,得它的两条对角线是☉O的两条直径,且这两条直径互相垂直.
所以只要在☉O内作两条互相垂直的直径AC和BD,就可以作出☉O的内接正方形ABCD.大展身手:大展身手:如图所示, ⊙O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交⊙O于点D,连接 BD,DC.
求证:BD=DC=DI证明:∵AI 平分∠BAC,
∴∠BAD=∠DAC,
∴弧BD=弧BC
∴BD=DC.
∵BI 平分∠ABC,
∴∠ABI=∠CBI.
∵∠BAD=∠DAC,∠DBC=∠DAC,
∴∠BAD=∠DBC.
又∵∠DBI=∠DBC+∠CBI,∠DIB=∠ABI+∠BAD,
∴∠DBI=∠DIB,
∴△BDI为等腰三角形,
∴BD=ID,
∴BD=DC=DI. 知识……方法……感悟……1.已知,四边形ABCD是⊙O的内接四边形,∠D=50°,则∠ABC等于( )
A.100° B.110° C.120° D.130°
2.如图,四边形ABCD是圆内接四边形,E是BC延长线上一点,若∠BAD=105°,则∠DCE的大小是( )
A.115° B.l05° C.100° D.95°DB3、如图,四边形ABCD是⊙O的内接四边形,∠B=130°,则∠AOC的度数是__ _度.1004、如图,点A,B,C,D都在⊙O上,∠ABC=90°,AD=3,CD=2,则⊙O的直径的长是____ .5、如图,四边形ABCD为圆的内接四边形,DA,CB的延长线交于点P,∠P=30°,∠ABC=100°,则∠C= 。?70°“方”是做人之本,是堂堂正正做人的脊梁,“圆”是处世之道,是妥妥当当处世的锦囊。一个人,如果过分方正,有棱有角,难免碰得头破血流;而一个人如果八面玲珑,圆滑透顶,总想自己占便宜,也必将众叛亲离。因此,做人必须方外有圆,圆内有方。
