鲁教版 九年级下册数学 5.6 直线和圆的位置关系(共19张ppt)
文档属性
| 名称 | 鲁教版 九年级下册数学 5.6 直线和圆的位置关系(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-24 23:12:05 | ||
图片预览





文档简介
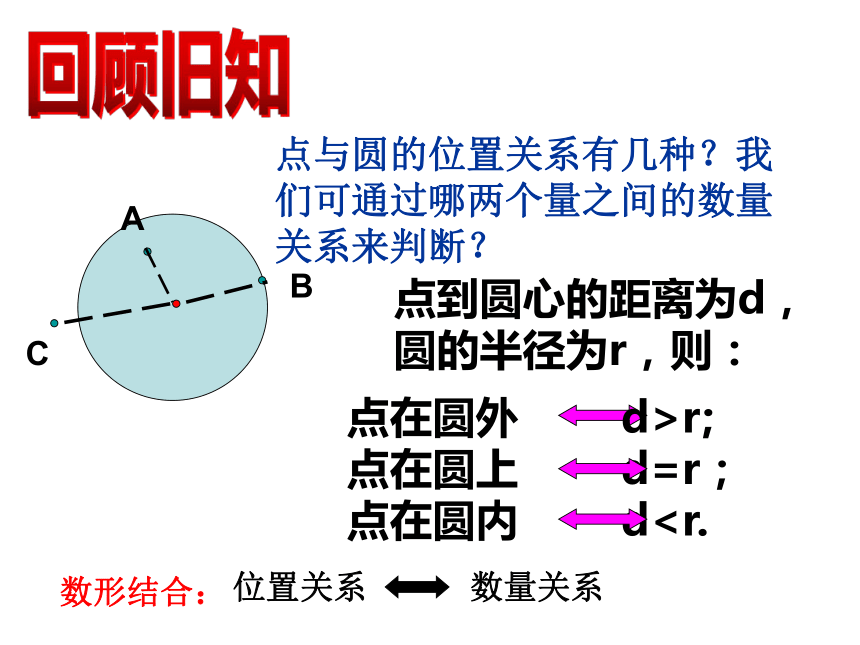
课件19张PPT。———————————————————直线和圆的位置关系点与圆的位置关系有几种?我们可通过哪两个量之间的数量关系来判断? 点到圆心的距离为d,圆的半径为r,则:回顾旧知点在圆外 d>r;
点在圆上 d=r;
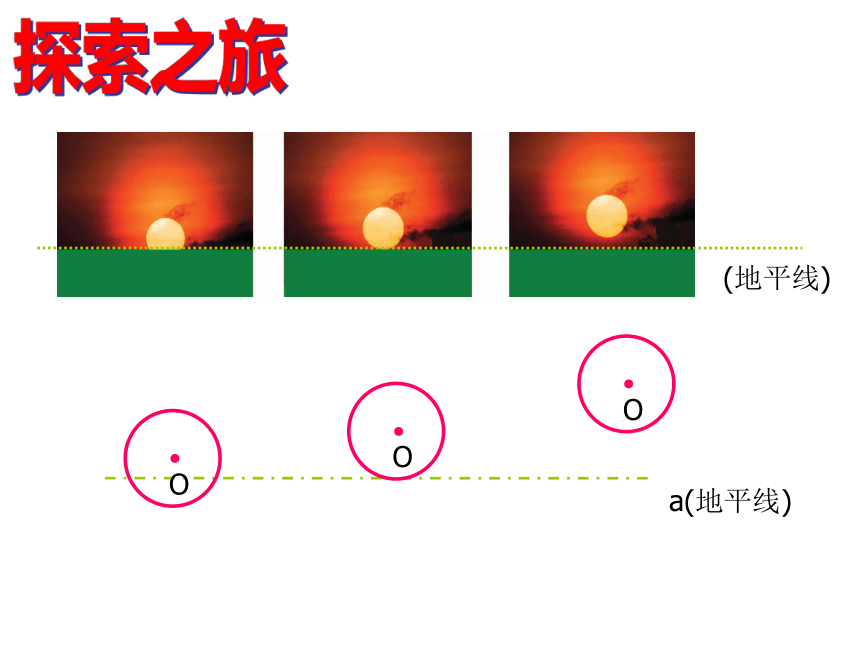
点在圆内 d位置关系数形结合:数量关系观察图片:火眼金睛火眼金睛火眼金睛 如果将太阳看成一个圆,将海平线看成一条直线,
请同学们利用手中的工具描绘出整个情景。
在描绘过程中,你认为直线与圆的位置关系可以分为哪几类?
你分类的依据是什么?探索之旅(地平线)a(地平线)探索之旅(2)直线和圆有唯一个公共点,
叫做直线和圆相切,
这条直线叫圆的切线,
这个公共点叫切点。(1)直线和圆有两个公共点,
叫做直线和圆相交,
这两个公共点叫交点。(3)直线和圆没有公共点时,
叫做直线和圆相离。归纳一、直线与圆的位置关系(用公共点的个数来区分)探索新知练习一:看图判断直线l与⊙O的位置关系(1)(2)(3)(4)(5)?lllll·O·O·O·O·O(5)?l 如果公共点的个数不好判断,该怎么办?·O联想类比: “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?直线和圆相交d< r直线和圆相切d= r直线和圆相离d> r数形结合:位置关系数量关系归纳二、直线和圆的位置关系(用圆心o到直线l的距离d与圆的半径r的关系来区分)总结:判定直线与圆的位置关系的方法有____种:(1)根据定义,由________________ 的个数来判断;(2)根据性质,由_________________ 的关系来判断。在实际应用中,常采用第二种方法判定。两直线与圆的公共点圆心到直线的距离d与半径r
相交相切相离d > 5cmd = 5cmd < 5cm小试牛刀0cm≤210学以致用:
在Rt△ABC中,∠C=90°,AB=8cm,AC=4cm,(1)以C为圆心作圆,当半径的长为多少时,AB与⊙C相切?
(2)以C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?d解:(1)如图,过C作CD⊥AB,垂足为D∵AC=4cm,AB=8cm
有d=r,因此?C和AB相切。d即圆心C到AB的距离d=2 cm所以当r=2 cm时,(2)当r=2cm时,有d>r,因此⊙C和AB相离。 当r=4cm时,有d(-3,-4),则x轴与?A的位置关系是_____, y轴与?A的位置关系是_____。相离相切拓展延伸.(-3,-4)OBC43-1-1若?A要与x轴相切,则?A该向上移动多少个单位?若?A要与x轴相交呢?变式训练相切:1个或7个
相交:1<移动的距离<7
点在圆上 d=r;
点在圆内 d
请同学们利用手中的工具描绘出整个情景。
在描绘过程中,你认为直线与圆的位置关系可以分为哪几类?
你分类的依据是什么?探索之旅(地平线)a(地平线)探索之旅(2)直线和圆有唯一个公共点,
叫做直线和圆相切,
这条直线叫圆的切线,
这个公共点叫切点。(1)直线和圆有两个公共点,
叫做直线和圆相交,
这两个公共点叫交点。(3)直线和圆没有公共点时,
叫做直线和圆相离。归纳一、直线与圆的位置关系(用公共点的个数来区分)探索新知练习一:看图判断直线l与⊙O的位置关系(1)(2)(3)(4)(5)?lllll·O·O·O·O·O(5)?l 如果公共点的个数不好判断,该怎么办?·O联想类比: “直线和圆的位置关系”能否像“点和圆的位置关系”一样进行数量分析?直线和圆相交d< r直线和圆相切d= r直线和圆相离d> r数形结合:位置关系数量关系归纳二、直线和圆的位置关系(用圆心o到直线l的距离d与圆的半径r的关系来区分)总结:判定直线与圆的位置关系的方法有____种:(1)根据定义,由________________ 的个数来判断;(2)根据性质,由_________________ 的关系来判断。在实际应用中,常采用第二种方法判定。两直线与圆的公共点圆心到直线的距离d与半径r
相交相切相离d > 5cmd = 5cmd < 5cm小试牛刀0cm≤210学以致用:
在Rt△ABC中,∠C=90°,AB=8cm,AC=4cm,(1)以C为圆心作圆,当半径的长为多少时,AB与⊙C相切?
(2)以C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?d解:(1)如图,过C作CD⊥AB,垂足为D∵AC=4cm,AB=8cm
有d=r,因此?C和AB相切。d即圆心C到AB的距离d=2 cm所以当r=2 cm时,(2)当r=2cm时,有d>r,因此⊙C和AB相离。 当r=4cm时,有d
相交:1<移动的距离<7
