鲁教版九年级下册数学5.7 切线长定理课件(共16张ppt)
文档属性
| 名称 | 鲁教版九年级下册数学5.7 切线长定理课件(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-25 00:00:00 | ||
图片预览




文档简介
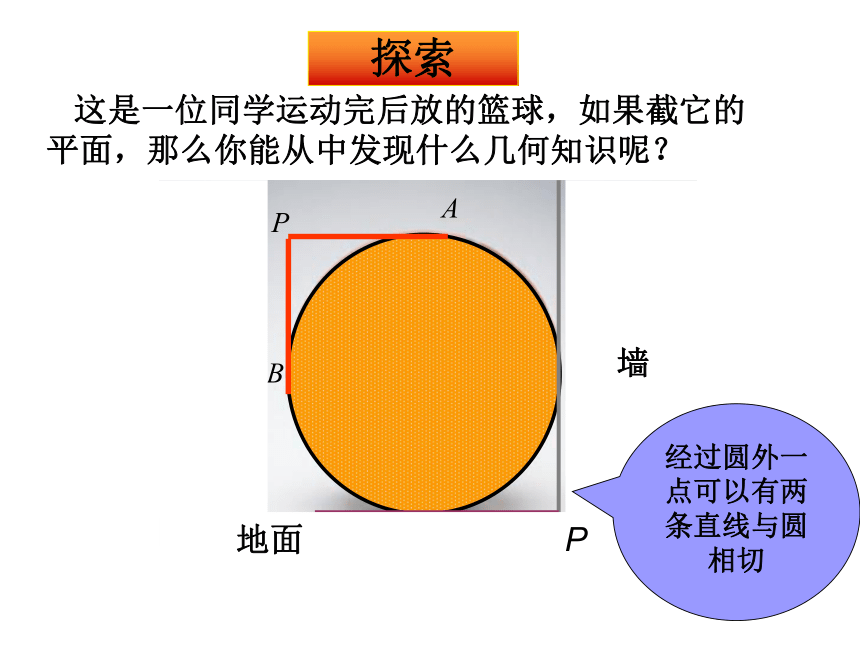
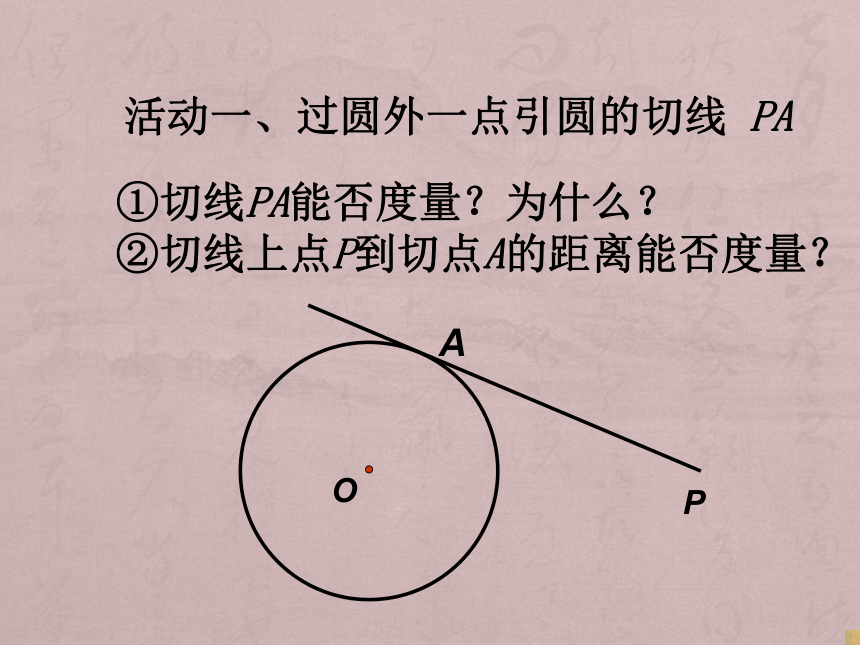
课件16张PPT。切线长定理(1)和圆有唯一公共点的直线叫 (2)圆的切线 过切点的半径。 (3)四边形ABCD各边都和⊙O相切,则四边形ABCD叫做这个圆的圆的切线垂直于外切四边形复习 这是一位同学运动完后放的篮球,如果截它的平面,那么你能从中发现什么几何知识呢?墙 地面 P经过圆外一点可以有两条直线与圆相切探索O①切线PA能否度量?为什么?
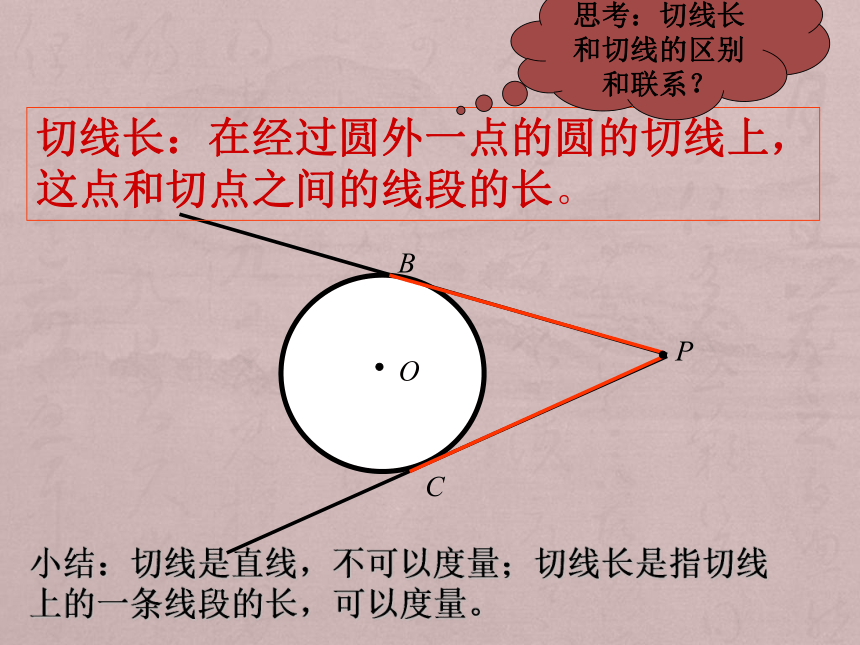
②切线上点P到切点A的距离能否度量?活动一、过圆外一点引圆的切线 PAPBCO切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长。思考:切线长和切线的区别和联系?小结:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。活动二、自主探究切线长定理观察、猜想切线长PA、PB大小有什么关系?∠APO与∠BPO有什么关系?
方法:1、测量。
2、对称性。
3、构造三角形证明全等。PA是⊙o的切线,如果将⊙o沿直线OP翻折,两半圆能否重合?
如果重合,设与A重合点为B,连接PB,
直线PB是否是⊙O切线?pABO已知: 求证:PA=PB ∠OPA=∠OPB如图,P为⊙ O外一点,PA、PB为⊙ O的切线,A、B为切点,连结PO你能不能用所
学的几何知识
证明刚才的实验?从你实验的观察和你的证明你能得出怎样的结论呢?O切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。pABO请你们结合图形用数学语言表达定理例1 已知如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求⊙O 的半径。拓展延伸一∵AC、BC分别切⊙O于E,F
∴CE=CF
同理 AD=AF BE=BD
∵AC切⊙O于F,OF为半径
∴∠OFC=90°
同理 ∠OEC=90°
又∵∠C=90°
∴∠C=∠OFC= ∠OEC
又∵OE=OF
∴四边形OECF为正方形
∴OE=CE=CF
设⊙O的半径r,OE=CE=CF=r
∵CE+BE=24
∴BE=24-r
∵ BE=BD
∴BD=24-r
同理 AD=10-r
∵BD+AD=AB
∴AB=24-r+10-r
即AB=34-2r
在Rt△ABC中由勾股定理得
AB 2=AC 2+BC 2
又∵ AC=10 BC=24
∴AB=26
又∵ AB=34-2r
∴34-2r=26
∴r=4
所以⊙O的半径是4.
变式1:如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点 D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长。变式2:如图,P是⊙O外一点,PA与PB分别⊙O切于A、B两点,DE也是⊙O的切线,切点为C,PA=PB=5cm,求△PDE的周长。ABDLMNPO结论:圆的外切四边形的两组对边和相等。已知:四边形ABCD的边 AB,BC,CD,DA和圆O分别相切于L,M,N,P。探索圆外切四边形边的关系。C(1)找出图中所有相等的线段(2)填空:AB+CD AD+BC(>,<,=)=DN=DP,AP=AL,BL=BM,CN=CM比较圆的内接四边形的性质:拓展延伸二一判断
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等( )
堂堂清25°二填空××(2)如图,Δ ABC的内切圆分别和BC,AC,AB切于D,E,F;如果AF=2cm,BD=7cm,CE=4cm,则BC= ,AC= AB= 三、如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知Δ PDE的周长为8,则P到⊙O的切线长PA的长为多少?
AP11cm6cm9cmBDO1、本节学习了切线长的定义,注意和切线比较。学习了切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。3、希望同学们在以后的学习中要勇于探索和实践,养成科学的学习态度。同时还要注意总结作辅助线的方法,和解题时要注意运用“数形结合”的思想方法。小结2、记住圆外切四边形的性质,并比较圆内接四边形
②切线上点P到切点A的距离能否度量?活动一、过圆外一点引圆的切线 PAPBCO切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长。思考:切线长和切线的区别和联系?小结:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。活动二、自主探究切线长定理观察、猜想切线长PA、PB大小有什么关系?∠APO与∠BPO有什么关系?
方法:1、测量。
2、对称性。
3、构造三角形证明全等。PA是⊙o的切线,如果将⊙o沿直线OP翻折,两半圆能否重合?
如果重合,设与A重合点为B,连接PB,
直线PB是否是⊙O切线?pABO已知: 求证:PA=PB ∠OPA=∠OPB如图,P为⊙ O外一点,PA、PB为⊙ O的切线,A、B为切点,连结PO你能不能用所
学的几何知识
证明刚才的实验?从你实验的观察和你的证明你能得出怎样的结论呢?O切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。pABO请你们结合图形用数学语言表达定理例1 已知如图,Rt△ABC的两条直角边AC=10,BC=24,⊙O 是△ABC 的内切圆,切点分别为D,E,F,求⊙O 的半径。拓展延伸一∵AC、BC分别切⊙O于E,F
∴CE=CF
同理 AD=AF BE=BD
∵AC切⊙O于F,OF为半径
∴∠OFC=90°
同理 ∠OEC=90°
又∵∠C=90°
∴∠C=∠OFC= ∠OEC
又∵OE=OF
∴四边形OECF为正方形
∴OE=CE=CF
设⊙O的半径r,OE=CE=CF=r
∵CE+BE=24
∴BE=24-r
∵ BE=BD
∴BD=24-r
同理 AD=10-r
∵BD+AD=AB
∴AB=24-r+10-r
即AB=34-2r
在Rt△ABC中由勾股定理得
AB 2=AC 2+BC 2
又∵ AC=10 BC=24
∴AB=26
又∵ AB=34-2r
∴34-2r=26
∴r=4
所以⊙O的半径是4.
变式1:如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点 D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长。变式2:如图,P是⊙O外一点,PA与PB分别⊙O切于A、B两点,DE也是⊙O的切线,切点为C,PA=PB=5cm,求△PDE的周长。ABDLMNPO结论:圆的外切四边形的两组对边和相等。已知:四边形ABCD的边 AB,BC,CD,DA和圆O分别相切于L,M,N,P。探索圆外切四边形边的关系。C(1)找出图中所有相等的线段(2)填空:AB+CD AD+BC(>,<,=)=DN=DP,AP=AL,BL=BM,CN=CM比较圆的内接四边形的性质:拓展延伸二一判断
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等( )
堂堂清25°二填空××(2)如图,Δ ABC的内切圆分别和BC,AC,AB切于D,E,F;如果AF=2cm,BD=7cm,CE=4cm,则BC= ,AC= AB= 三、如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知Δ PDE的周长为8,则P到⊙O的切线长PA的长为多少?
AP11cm6cm9cmBDO1、本节学习了切线长的定义,注意和切线比较。学习了切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。3、希望同学们在以后的学习中要勇于探索和实践,养成科学的学习态度。同时还要注意总结作辅助线的方法,和解题时要注意运用“数形结合”的思想方法。小结2、记住圆外切四边形的性质,并比较圆内接四边形
