2019人教版高中数学必修三课件:第三章 本章总结提升(共25张PPT)
文档属性
| 名称 | 2019人教版高中数学必修三课件:第三章 本章总结提升(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-24 12:49:16 | ||
图片预览






文档简介
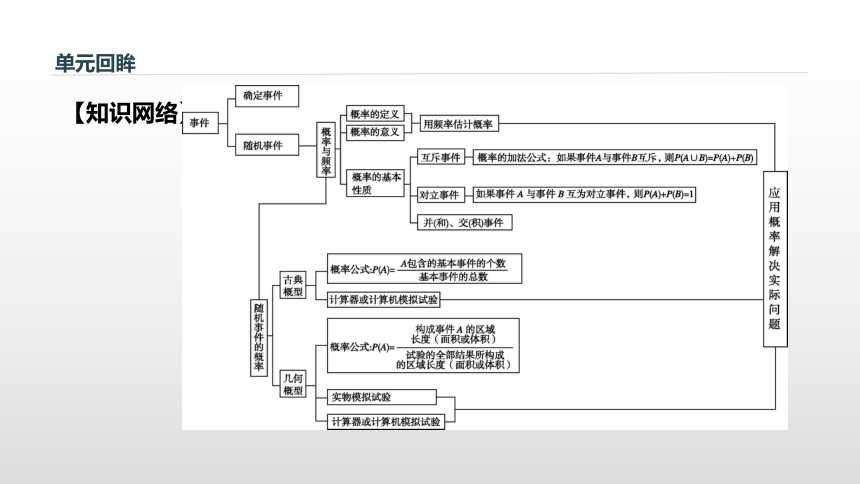
课件25张PPT。第三章 概率本章总结提升 单元回眸【知识网络】判断下列说法是否正确.(请在括号中填写“√”或“×”)
1.“方程x2+2x+8=0有两个实根”是不可能事件.( )
2.在大量重复试验中,概率是频率的稳定值. ( )
3.对立事件一定是互斥事件,互斥事件不一定是对立事件.( )
4.两个事件的和事件是指两个事件都发生的事件. ( )
5.“在适宜条件下种下一粒种子,观察它是否发芽”属于古典概型,其基本事件是“发芽”与“不发芽”.( )
6.掷一枚质地均匀的硬币两次,出现“两个正面”“一正一反”“两个反面”这三个结果的可能性是相等的.( )单元回眸【知识辨析】√××√√×?单元回眸√√√√整合创新互斥事件与对立事件的概率及应用题型一 [类型总述] (1)随机事件的频率与概率;(2)随机事件的关系与运算;(3)互斥事件;
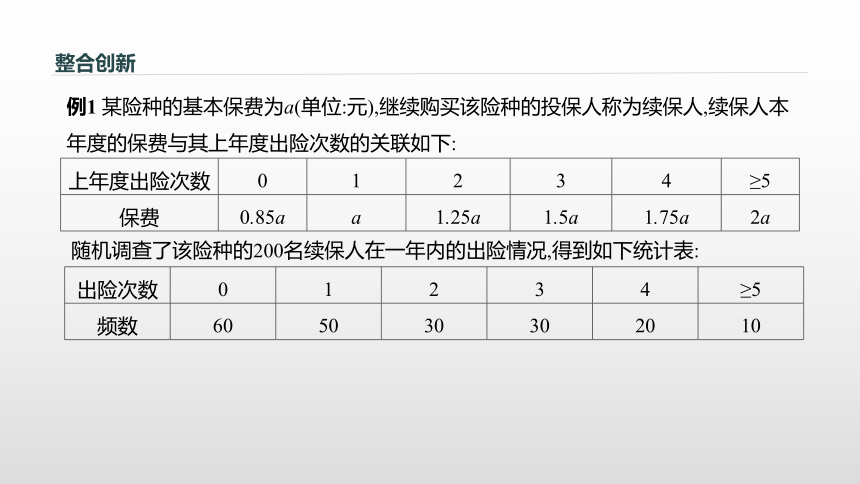
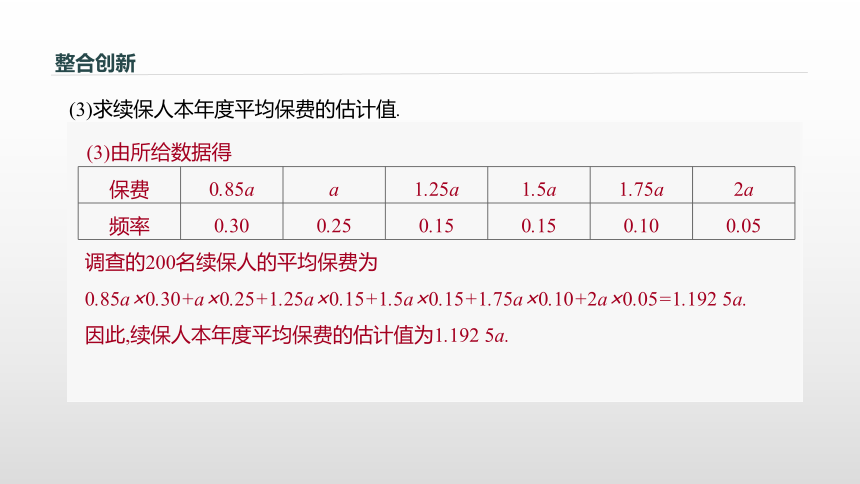
(4)对立事件.整合创新例1 某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:整合创新(1)记A为事件“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;?整合创新(2)记B为事件“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;?整合创新(3)求续保人本年度平均保费的估计值.(3)由所给数据得调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=1.192 5a.因此,续保人本年度平均保费的估计值为1.192 5a.整合创新变式 为备战奥运会,某射击运动员在相同条件下进行射击训练,结果如下表:
(1)该射击运动员射击一次,击中靶心的概率大约是多少?
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?
(3)假设该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗?整合创新解:(1)由表可知,击中靶心的频率在0.9附近,故击中靶心的概率大约是0.9.
(2)击中靶心的次数大约是300×0.9=270.
(3)由概率的意义可知概率是个常数,不因试验次数的变化而变化.最后一次击中靶心的概率仍大约是0.9,所以不一定击中靶心.整合创新例2 某商场有奖销售中,每购物满100元可抽取1张奖券,多购多得,每1000张奖券为一个开奖单位.设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)P(A),P(B),P(C);
(2)抽取1张奖券中奖的概率;
(3)抽取1张奖券不中特等奖或一等奖的概率.
整合创新?整合创新古典概型的概率求解题型二例3 [2018·天津卷] 已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
[类型总述] (1)基本事件的概率;(2)古典概型的概率公式.整合创新解:(1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人、2人、2人.整合创新?整合创新变式 某校老师在一次高一数学考试后,对90分(含90分)以上的成绩进行统计,其频率分布直方图如图T3-1所示(分组区间为[90,100),[100,110),[110,120),[120,130),[130,140]),成绩(单位:分)在[120,130)内的学生有30人.
图T3-1整合创新?(1)求在这次考试中,成绩不低于90分的学生人数;整合创新 (2)估计这次考试中,成绩不低于90分的学生的平均成绩为
95×0.1+105×0.25+115×0.45+125×0.15+135×0.05=113(分).(2)请根据频率分布直方图估计这次考试中,成绩不低于90分的学生的平均成绩;整合创新 (3)为进一步了解学生的学习情况,按分层抽样方法从成绩在[90,100)和成绩在[120,130)内的学生中抽出5人,从抽出的学生中选出2人分别进行问卷A和问卷B调查,求对成绩在[90,100)内的学生进行问卷A调查,成绩在[120,130)内的学生进行问卷B调查的概率.整合创新?整合创新几何概型的概率题型三?? [类型总述] (1)一维(长度、角度)几何概型的概率;(2)二维(面积)几何概型的概率.B图T3-2整合创新??B整合创新例4 (3)如图T3-3,在边长为1的正方形中,随机撒1000粒豆子,有180粒落到阴影部分,据此估计阴影部分的面积为 .?
?0.18图T3-3整合创新??B
1.“方程x2+2x+8=0有两个实根”是不可能事件.( )
2.在大量重复试验中,概率是频率的稳定值. ( )
3.对立事件一定是互斥事件,互斥事件不一定是对立事件.( )
4.两个事件的和事件是指两个事件都发生的事件. ( )
5.“在适宜条件下种下一粒种子,观察它是否发芽”属于古典概型,其基本事件是“发芽”与“不发芽”.( )
6.掷一枚质地均匀的硬币两次,出现“两个正面”“一正一反”“两个反面”这三个结果的可能性是相等的.( )单元回眸【知识辨析】√××√√×?单元回眸√√√√整合创新互斥事件与对立事件的概率及应用题型一 [类型总述] (1)随机事件的频率与概率;(2)随机事件的关系与运算;(3)互斥事件;
(4)对立事件.整合创新例1 某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:整合创新(1)记A为事件“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;?整合创新(2)记B为事件“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;?整合创新(3)求续保人本年度平均保费的估计值.(3)由所给数据得调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=1.192 5a.因此,续保人本年度平均保费的估计值为1.192 5a.整合创新变式 为备战奥运会,某射击运动员在相同条件下进行射击训练,结果如下表:
(1)该射击运动员射击一次,击中靶心的概率大约是多少?
(2)假设该射击运动员射击了300次,则击中靶心的次数大约是多少?
(3)假设该射击运动员射击了10次,前9次中有8次击中靶心,那么第10次一定击中靶心吗?整合创新解:(1)由表可知,击中靶心的频率在0.9附近,故击中靶心的概率大约是0.9.
(2)击中靶心的次数大约是300×0.9=270.
(3)由概率的意义可知概率是个常数,不因试验次数的变化而变化.最后一次击中靶心的概率仍大约是0.9,所以不一定击中靶心.整合创新例2 某商场有奖销售中,每购物满100元可抽取1张奖券,多购多得,每1000张奖券为一个开奖单位.设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A,B,C,求:
(1)P(A),P(B),P(C);
(2)抽取1张奖券中奖的概率;
(3)抽取1张奖券不中特等奖或一等奖的概率.
整合创新?整合创新古典概型的概率求解题型二例3 [2018·天津卷] 已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
[类型总述] (1)基本事件的概率;(2)古典概型的概率公式.整合创新解:(1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人、2人、2人.整合创新?整合创新变式 某校老师在一次高一数学考试后,对90分(含90分)以上的成绩进行统计,其频率分布直方图如图T3-1所示(分组区间为[90,100),[100,110),[110,120),[120,130),[130,140]),成绩(单位:分)在[120,130)内的学生有30人.
图T3-1整合创新?(1)求在这次考试中,成绩不低于90分的学生人数;整合创新 (2)估计这次考试中,成绩不低于90分的学生的平均成绩为
95×0.1+105×0.25+115×0.45+125×0.15+135×0.05=113(分).(2)请根据频率分布直方图估计这次考试中,成绩不低于90分的学生的平均成绩;整合创新 (3)为进一步了解学生的学习情况,按分层抽样方法从成绩在[90,100)和成绩在[120,130)内的学生中抽出5人,从抽出的学生中选出2人分别进行问卷A和问卷B调查,求对成绩在[90,100)内的学生进行问卷A调查,成绩在[120,130)内的学生进行问卷B调查的概率.整合创新?整合创新几何概型的概率题型三?? [类型总述] (1)一维(长度、角度)几何概型的概率;(2)二维(面积)几何概型的概率.B图T3-2整合创新??B整合创新例4 (3)如图T3-3,在边长为1的正方形中,随机撒1000粒豆子,有180粒落到阴影部分,据此估计阴影部分的面积为 .?
?0.18图T3-3整合创新??B
