江苏省盐城市2018~2019学年第二学期期末考试高二数学试卷文理合卷(含答案)
文档属性
| 名称 | 江苏省盐城市2018~2019学年第二学期期末考试高二数学试卷文理合卷(含答案) | 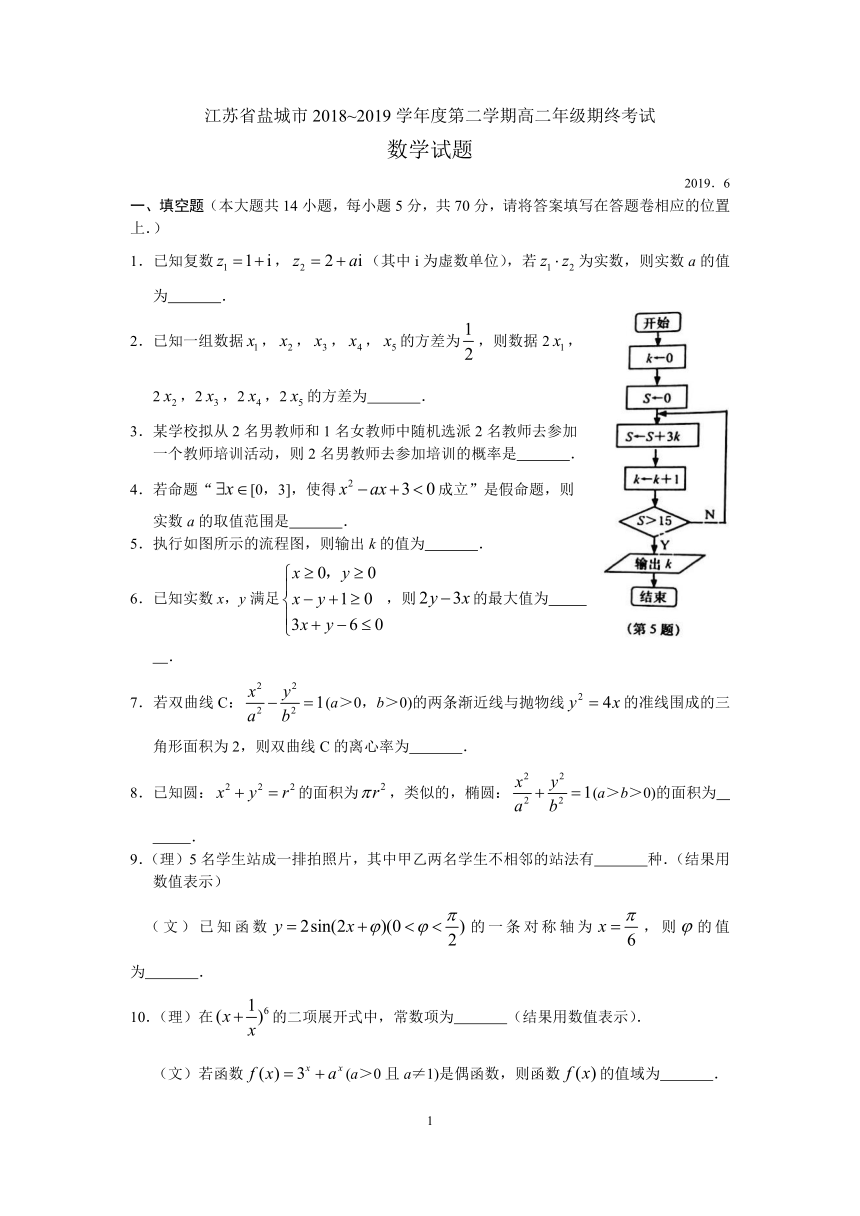 | |
| 格式 | zip | ||
| 文件大小 | 555.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-06-24 18:14:41 | ||
图片预览




文档简介
江苏省盐城市2018~2019学年度第二学期高二年级期终考试
数学试题
2019.6
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上.)
1.已知复数,(其中i为虚数单位),若为实数,则实数a的值为 .
2.已知一组数据,,,,的方差为,则数据2,
2,2,2,2的方差为 .
3.某学校拟从2名男教师和1名女教师中随机选派2名教师去参加
一个教师培训活动,则2名男教师去参加培训的概率是 .
4.若命题“[0,3],使得成立”是假命题,则
实数a的取值范围是 .
5.执行如图所示的流程图,则输出k的值为 .
6.已知实数x,y满足,则的最大值为
.
7.若双曲线C:(a>0,b>0)的两条渐近线与抛物线的准线围成的三角形面积为2,则双曲线C的离心率为 .
8.已知圆:的面积为,类似的,椭圆:(a>b>0)的面积为
.
9.(理)5名学生站成一排拍照片,其中甲乙两名学生不相邻的站法有 种.(结果用数值表示)
(文)已知函数的一条对称轴为,则的值为 .
10.(理)在的二项展开式中,常数项为 (结果用数值表示).
(文)若函数(a>0且a≠1)是偶函数,则函数的值域为 .
11.已知函数,则“a>0”是“函数有且仅有一个极值点”的 条件.(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
12.设A,B分别为椭圆C:(a>b>0)的右顶点和上顶点,已知椭圆C过点P(2,1),当线段AB长最小时椭圆C的离心率为 .
13.若x,y为正实数,则的最大值为 .
14.已知函数([1,2])的最大值为4,则实数a的值为 .
二、解答题(本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.)
15.(本小题满分14分)
(理)如图,在四棱锥P—ABCD中,已知底面ABCD为菱形,AC=8,BD=6,O为对角线AC与BD的交点,PO⊥底面ABCD且PO=4.
(1)求异面直线PA与BC所成角的余弦值;
(2)求平面APC与平面PCB所成锐二面角的余弦值.
/
(文)设命题p:函数在[﹣1,0]是减函数;命题q:[0,],都有≤1成立.
(1)若命题p为真命题,求实数m的取值范围;
(2)若pq为真命题,pq为假命题,求实数m的取值范围.
16.(本小题满分14分)
(理)某超市在节日期间进行有奖促销,凡在该超市购物满200元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有5只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励20元;共两只球都是绿色,则奖励10元;若两只球颜色不同,则不奖励.
(1)求一名顾客在一次摸奖活动中获得20元的概率;
(2)记X为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量X的分布列和数学期望.
(文)设函数.
(1)若函数为奇函数,(0,),求的值;
(2)若=,=,(0,),求的值.
17.(本小题满分14分)
(理)已知数列各项均为正数,满足.
(1)求,,的值;
(2)猜想数列的通项公式,并用数学归纳法证明你的结论.
(文)设,R.
(1)证明:对任意实数k,函数都不是奇函数;
(2)当k=时,求函数的单调递增区间.
18.(本小题满分16分)
如图,一条小河岸边有相距8km的A,B两个村庄(村庄视为岸边上A,B两点),在小河另一侧有一集镇P(集镇视为点P),P到岸边的距离PQ为2km,河宽OH为0.05km,通过测量可知,∠PAB与∠PBA的正切值之比为1:3.当地政府为方便村民出行,拟在小河上建一座桥MN(M,N分别为两岸上的点,且MN垂直河岸,M在Q的左侧),建桥要求:两村所有人到集镇所走距离之和最短,已知A,B两村的人口数分别是1000人、500人,假设一年中每人去集镇的次数均为m次.设∠PMQ=.(小河河岸视为两条平行直线)
(1)记L为一年中两村所有人到集镇所走距离之和,试用表示L;
(2)试确定的余弦值,使得L最小,从而符合建桥要求.
/
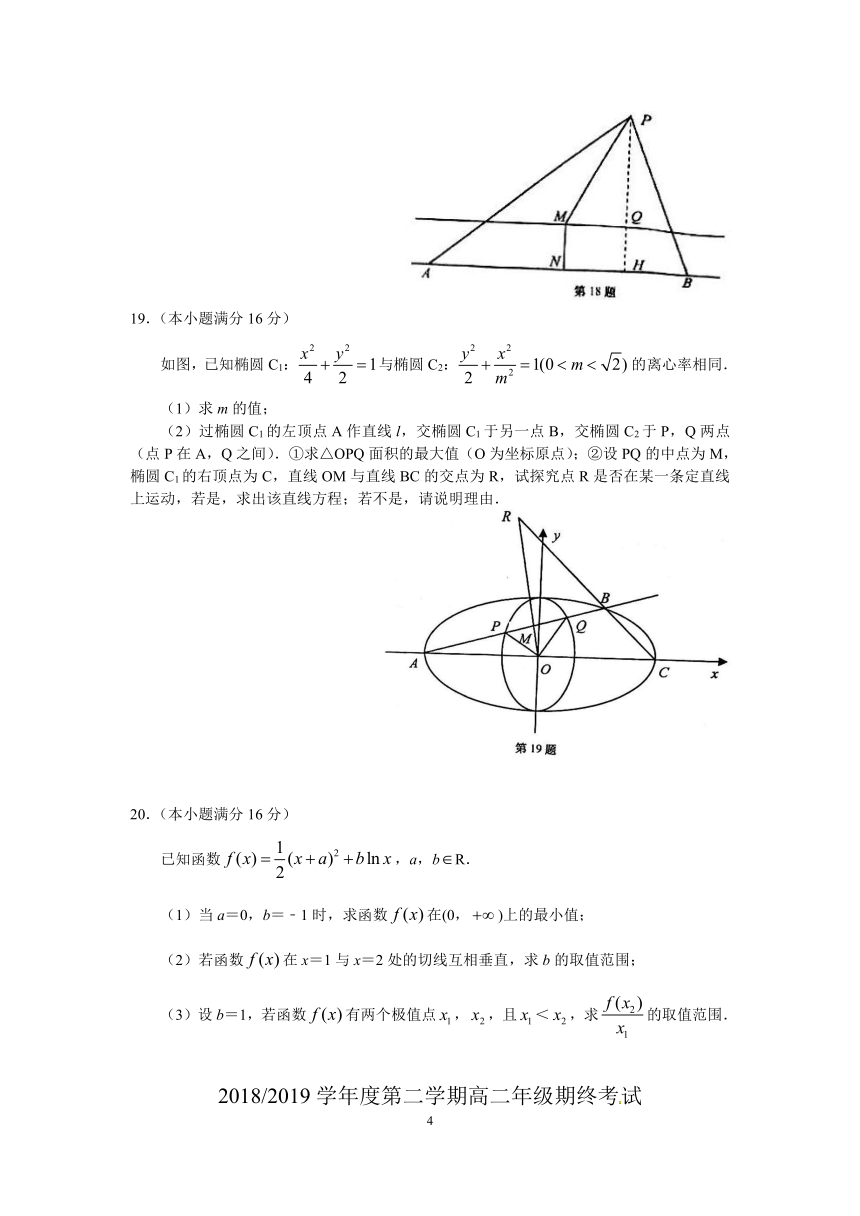
19.(本小题满分16分)
如图,已知椭圆C1:与椭圆C2:的离心率相同.
(1)求m的值;
(2)过椭圆C1的左顶点A作直线l,交椭圆C1于另一点B,交椭圆C2于P,Q两点(点P在A,Q之间).①求△OPQ面积的最大值(O为坐标原点);②设PQ的中点为M,椭圆C1的右顶点为C,直线OM与直线BC的交点为R,试探究点R是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
/
20.(本小题满分16分)
已知函数,a,bR.
(1)当a=0,b=﹣1时,求函数在(0,)上的最小值;
(2)若函数在x=1与x=2处的切线互相垂直,求b的取值范围;
(3)设b=1,若函数有两个极值点,,且<,求的取值范围.
2018/2019学年度第二学期高二年级期终考/试
数学参考答案
一.填空题
1. 2. 3. 4. 5. 6. 7. 8. 9.(理)(文)
10.(理)(文) 11.充分不必要 12. 13. 14.
二.解答题
15.(理科)
因为底面为菱形,,,底面,
所以,以所在直线分别为轴建立空间直角坐标系
(如图所示),则……………………………2分
设为直线所成的角,
,
=,
所以异面直线与所成角的余弦值为………………………………………6分
因为平面,所以平面的法向量取,………………8分
设平面的法向量为,,
则由,
即,取,…………………………………………………12分
设为两个平面所成的锐二面角的平面角,则,
所以平面与平面所成锐二面角的余弦值为………………………14分
(文科)
为真:因为函数是减函数,
所以在上恒成立,………………………………………2分
所以,所以……………………………………………………………4分
(2)为真:因为对恒成立,
所以对恒成立,
因为,
所以,………………………………………………………………8分
当真假即,
所以………………………………………………………………………………10分
当真假即且,
所以……………………………………………………………………………12分
综上或……………………………………………………………14分
16.(理科)解:(1)记一名顾客摸球中奖20元为事件,
则.………………………………………………………………………2分
(2)记一名顾客摸球中奖10元为事件,不中奖为事件,
则,,…………………………………4分
所以,
,
,
,
,…………………………………12分
X
0
10
20
30
40
p
所以…………………14分
(文科)解:(1)因为函数为奇函数,
所以,
又,所以,………………………………………………………………2分
当时,是奇函数,
所以.………………………………………………………………………………4分
(2)
因为,,所以,
又,
所以,,…………………6分
所以,
……………10分
所以……………………………………12分
所以.
………………14分
17(理)解:(1)当时,,又,所以,
当时,,解得,
当时,,解得.………………………………2分
(2)猜想:.……………………………………………………………………4分
证明:(1)当时,由(1)可知结论成立;………………………………6分
(2)假设当时,结论成立,即成立,………………………8分
则时,
由与,
所以,
所以,
又,成立,…………………………………………12分
根据(1)、(2)猜想成立.………………………………………………14分
(文)证明:(1)假设函数为奇函数,则,
这与矛盾,
所以函数不可能是奇函数.…………………………4分
解:(2)当时,,
所以,,
所以在单调递增,………………………10分
又,
所以不等式的解集为,
所以函数的单调递增区间为.…………………………14分
18.解:(1)因与的正切值之比为,
所以,所以,即,……………2分
因,所以,,…………………………………4分
所以,
所以,
化简得,.……………………………7分
(2)由(1)知,
所以,
化简得,
由,得,……………………………………………………………10分
令,且,
当时,,;当时,,;
所以函数在上单调递减;在上单调递增;
所以时函数取最小值,即当时,符合建桥要求,……………14分
答:(1),;
(2)当时,符合建桥要求.……………………………………………16分
19.(1) 椭圆中,又,
所以,离心率………………………………………………2分
又椭圆中,又,
所以,
=,又因为,
所以………………………………………………………4分
(2)当直线与轴重合时,三点共线,不符合题意
故设直线的方程为:且
设
由(1)知椭圆的方程为:
联立方程消去得即
解得()
又
…………………………………………8分
令
此时………………10分
(3)由(2)知所以
所以
所以直线的斜率
直线的方程为…………………………………12分
联立方程消去得
得
所以
所以…………………………………14分
则直线的方程为
联立直线的方程解得点坐标为
所以点在定直线上运动.……………………………………16分
20. 解:
当时,,
,由得,
所以函数在区间单调递减,在区间单调递增,
…………………………………………………………………3分
由函数得
因为函数在与处的切线互相垂直,所以
即,…………………………………………………………5分
法一. 展开整理得,
该关于的方程有解,所以,
即,
所以或,…………………………………………………………………………9分
法二. 由,……………………………………………………5分
即,
所以,
即,所以或……………………………………………………9分
当时,,
所以是方程的两根,从而,………………10分
因为且,
所以,,
,…………………………………………12分
记
因为在单调递增,所以,
从而在单调递增,
所以……………………………………………………14分
又因为,
所以的取值范围为……………………………………………………16分
数学试题
2019.6
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上.)
1.已知复数,(其中i为虚数单位),若为实数,则实数a的值为 .
2.已知一组数据,,,,的方差为,则数据2,
2,2,2,2的方差为 .
3.某学校拟从2名男教师和1名女教师中随机选派2名教师去参加
一个教师培训活动,则2名男教师去参加培训的概率是 .
4.若命题“[0,3],使得成立”是假命题,则
实数a的取值范围是 .
5.执行如图所示的流程图,则输出k的值为 .
6.已知实数x,y满足,则的最大值为
.
7.若双曲线C:(a>0,b>0)的两条渐近线与抛物线的准线围成的三角形面积为2,则双曲线C的离心率为 .
8.已知圆:的面积为,类似的,椭圆:(a>b>0)的面积为
.
9.(理)5名学生站成一排拍照片,其中甲乙两名学生不相邻的站法有 种.(结果用数值表示)
(文)已知函数的一条对称轴为,则的值为 .
10.(理)在的二项展开式中,常数项为 (结果用数值表示).
(文)若函数(a>0且a≠1)是偶函数,则函数的值域为 .
11.已知函数,则“a>0”是“函数有且仅有一个极值点”的 条件.(选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
12.设A,B分别为椭圆C:(a>b>0)的右顶点和上顶点,已知椭圆C过点P(2,1),当线段AB长最小时椭圆C的离心率为 .
13.若x,y为正实数,则的最大值为 .
14.已知函数([1,2])的最大值为4,则实数a的值为 .
二、解答题(本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.)
15.(本小题满分14分)
(理)如图,在四棱锥P—ABCD中,已知底面ABCD为菱形,AC=8,BD=6,O为对角线AC与BD的交点,PO⊥底面ABCD且PO=4.
(1)求异面直线PA与BC所成角的余弦值;
(2)求平面APC与平面PCB所成锐二面角的余弦值.
/
(文)设命题p:函数在[﹣1,0]是减函数;命题q:[0,],都有≤1成立.
(1)若命题p为真命题,求实数m的取值范围;
(2)若pq为真命题,pq为假命题,求实数m的取值范围.
16.(本小题满分14分)
(理)某超市在节日期间进行有奖促销,凡在该超市购物满200元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有5只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励20元;共两只球都是绿色,则奖励10元;若两只球颜色不同,则不奖励.
(1)求一名顾客在一次摸奖活动中获得20元的概率;
(2)记X为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量X的分布列和数学期望.
(文)设函数.
(1)若函数为奇函数,(0,),求的值;
(2)若=,=,(0,),求的值.
17.(本小题满分14分)
(理)已知数列各项均为正数,满足.
(1)求,,的值;
(2)猜想数列的通项公式,并用数学归纳法证明你的结论.
(文)设,R.
(1)证明:对任意实数k,函数都不是奇函数;
(2)当k=时,求函数的单调递增区间.
18.(本小题满分16分)
如图,一条小河岸边有相距8km的A,B两个村庄(村庄视为岸边上A,B两点),在小河另一侧有一集镇P(集镇视为点P),P到岸边的距离PQ为2km,河宽OH为0.05km,通过测量可知,∠PAB与∠PBA的正切值之比为1:3.当地政府为方便村民出行,拟在小河上建一座桥MN(M,N分别为两岸上的点,且MN垂直河岸,M在Q的左侧),建桥要求:两村所有人到集镇所走距离之和最短,已知A,B两村的人口数分别是1000人、500人,假设一年中每人去集镇的次数均为m次.设∠PMQ=.(小河河岸视为两条平行直线)
(1)记L为一年中两村所有人到集镇所走距离之和,试用表示L;
(2)试确定的余弦值,使得L最小,从而符合建桥要求.
/
19.(本小题满分16分)
如图,已知椭圆C1:与椭圆C2:的离心率相同.
(1)求m的值;
(2)过椭圆C1的左顶点A作直线l,交椭圆C1于另一点B,交椭圆C2于P,Q两点(点P在A,Q之间).①求△OPQ面积的最大值(O为坐标原点);②设PQ的中点为M,椭圆C1的右顶点为C,直线OM与直线BC的交点为R,试探究点R是否在某一条定直线上运动,若是,求出该直线方程;若不是,请说明理由.
/
20.(本小题满分16分)
已知函数,a,bR.
(1)当a=0,b=﹣1时,求函数在(0,)上的最小值;
(2)若函数在x=1与x=2处的切线互相垂直,求b的取值范围;
(3)设b=1,若函数有两个极值点,,且<,求的取值范围.
2018/2019学年度第二学期高二年级期终考/试
数学参考答案
一.填空题
1. 2. 3. 4. 5. 6. 7. 8. 9.(理)(文)
10.(理)(文) 11.充分不必要 12. 13. 14.
二.解答题
15.(理科)
因为底面为菱形,,,底面,
所以,以所在直线分别为轴建立空间直角坐标系
(如图所示),则……………………………2分
设为直线所成的角,
,
=,
所以异面直线与所成角的余弦值为………………………………………6分
因为平面,所以平面的法向量取,………………8分
设平面的法向量为,,
则由,
即,取,…………………………………………………12分
设为两个平面所成的锐二面角的平面角,则,
所以平面与平面所成锐二面角的余弦值为………………………14分
(文科)
为真:因为函数是减函数,
所以在上恒成立,………………………………………2分
所以,所以……………………………………………………………4分
(2)为真:因为对恒成立,
所以对恒成立,
因为,
所以,………………………………………………………………8分
当真假即,
所以………………………………………………………………………………10分
当真假即且,
所以……………………………………………………………………………12分
综上或……………………………………………………………14分
16.(理科)解:(1)记一名顾客摸球中奖20元为事件,
则.………………………………………………………………………2分
(2)记一名顾客摸球中奖10元为事件,不中奖为事件,
则,,…………………………………4分
所以,
,
,
,
,…………………………………12分
X
0
10
20
30
40
p
所以…………………14分
(文科)解:(1)因为函数为奇函数,
所以,
又,所以,………………………………………………………………2分
当时,是奇函数,
所以.………………………………………………………………………………4分
(2)
因为,,所以,
又,
所以,,…………………6分
所以,
……………10分
所以……………………………………12分
所以.
………………14分
17(理)解:(1)当时,,又,所以,
当时,,解得,
当时,,解得.………………………………2分
(2)猜想:.……………………………………………………………………4分
证明:(1)当时,由(1)可知结论成立;………………………………6分
(2)假设当时,结论成立,即成立,………………………8分
则时,
由与,
所以,
所以,
又,成立,…………………………………………12分
根据(1)、(2)猜想成立.………………………………………………14分
(文)证明:(1)假设函数为奇函数,则,
这与矛盾,
所以函数不可能是奇函数.…………………………4分
解:(2)当时,,
所以,,
所以在单调递增,………………………10分
又,
所以不等式的解集为,
所以函数的单调递增区间为.…………………………14分
18.解:(1)因与的正切值之比为,
所以,所以,即,……………2分
因,所以,,…………………………………4分
所以,
所以,
化简得,.……………………………7分
(2)由(1)知,
所以,
化简得,
由,得,……………………………………………………………10分
令,且,
当时,,;当时,,;
所以函数在上单调递减;在上单调递增;
所以时函数取最小值,即当时,符合建桥要求,……………14分
答:(1),;
(2)当时,符合建桥要求.……………………………………………16分
19.(1) 椭圆中,又,
所以,离心率………………………………………………2分
又椭圆中,又,
所以,
=,又因为,
所以………………………………………………………4分
(2)当直线与轴重合时,三点共线,不符合题意
故设直线的方程为:且
设
由(1)知椭圆的方程为:
联立方程消去得即
解得()
又
…………………………………………8分
令
此时………………10分
(3)由(2)知所以
所以
所以直线的斜率
直线的方程为…………………………………12分
联立方程消去得
得
所以
所以…………………………………14分
则直线的方程为
联立直线的方程解得点坐标为
所以点在定直线上运动.……………………………………16分
20. 解:
当时,,
,由得,
所以函数在区间单调递减,在区间单调递增,
…………………………………………………………………3分
由函数得
因为函数在与处的切线互相垂直,所以
即,…………………………………………………………5分
法一. 展开整理得,
该关于的方程有解,所以,
即,
所以或,…………………………………………………………………………9分
法二. 由,……………………………………………………5分
即,
所以,
即,所以或……………………………………………………9分
当时,,
所以是方程的两根,从而,………………10分
因为且,
所以,,
,…………………………………………12分
记
因为在单调递增,所以,
从而在单调递增,
所以……………………………………………………14分
又因为,
所以的取值范围为……………………………………………………16分
同课章节目录
